红黑树规则
- 1.节点分为红色或者黑色;
- 2.根节点必为黑色;
- 3.叶子节点都为黑色,且为null;
- 4.连接红色节点的两个子节点都为黑色(红黑树不会出现相邻的红色节点);
- 5.从任意节点出发,到其每个叶子节点的路径中包含相同数量的黑色节点;
- 6.新加入到红黑树的节点为红色节点;
时间复杂度
查找跟插入都是 log(n)
变化规律
1.父节点是黑色,直接插入,不用做任何操作,因为默认插入是红色节点
2.父节点是红色:有三种情况
2.1父节点是红色,情况一:叔父节点为空
例子
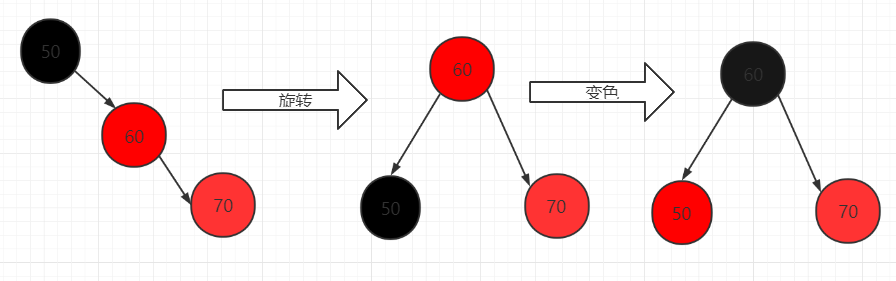
- 情况:现在树上有了 50,60,插入 70,默认新节点为红色,发现 60跟70都是红色 违法了红黑树相邻节点不能都为红色
- 解决:1.旋转 + 变色
2.2,情况二:叔父节点为红色
例子
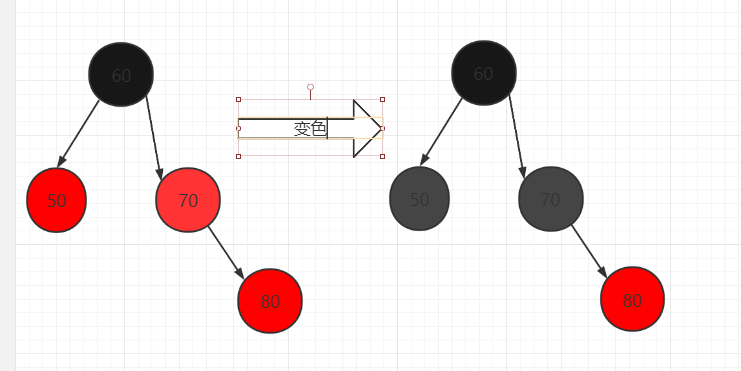
- 情况:节点现在又 50,60,70,加入80,默认红色节点,发现70跟80都是红色,违法红黑树相邻节点不能都为红色
- 解决:变色
2.3父节点是红色,情况三:叔父节点为黑色
例子:
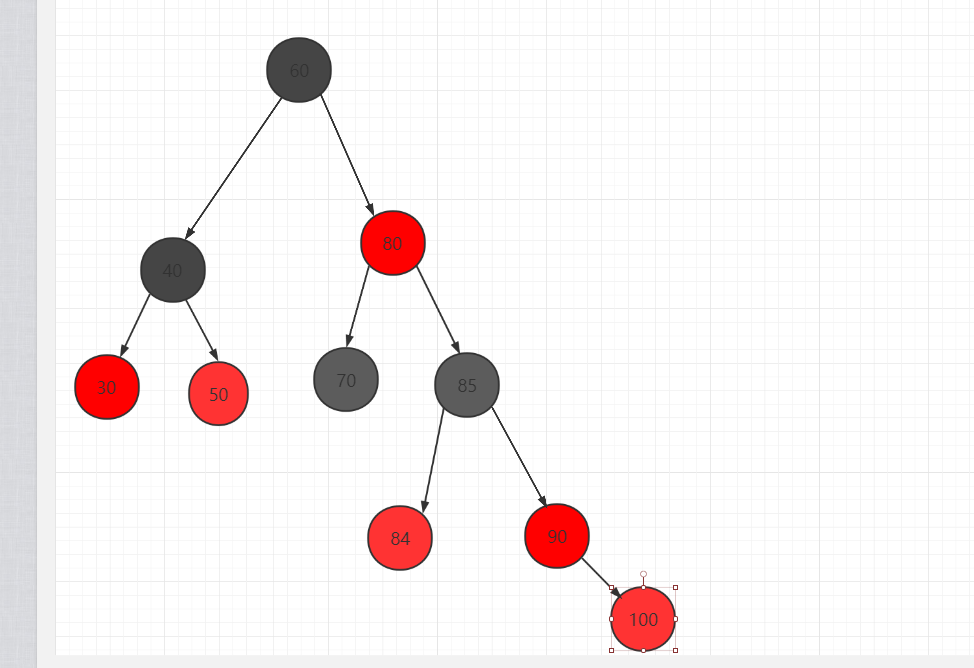
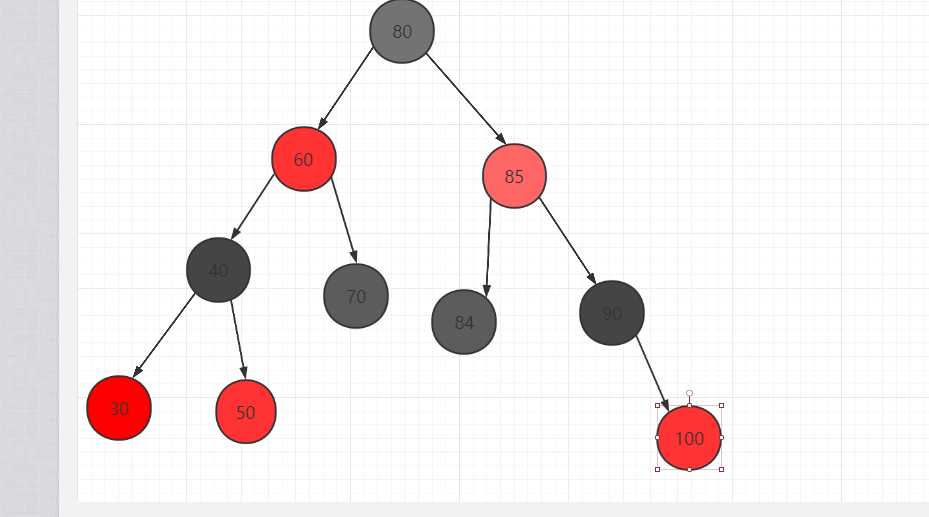
- 情况:在图1的情况下插入100此时100跟90同时红色,违法了红黑树相邻节点不能都为红色
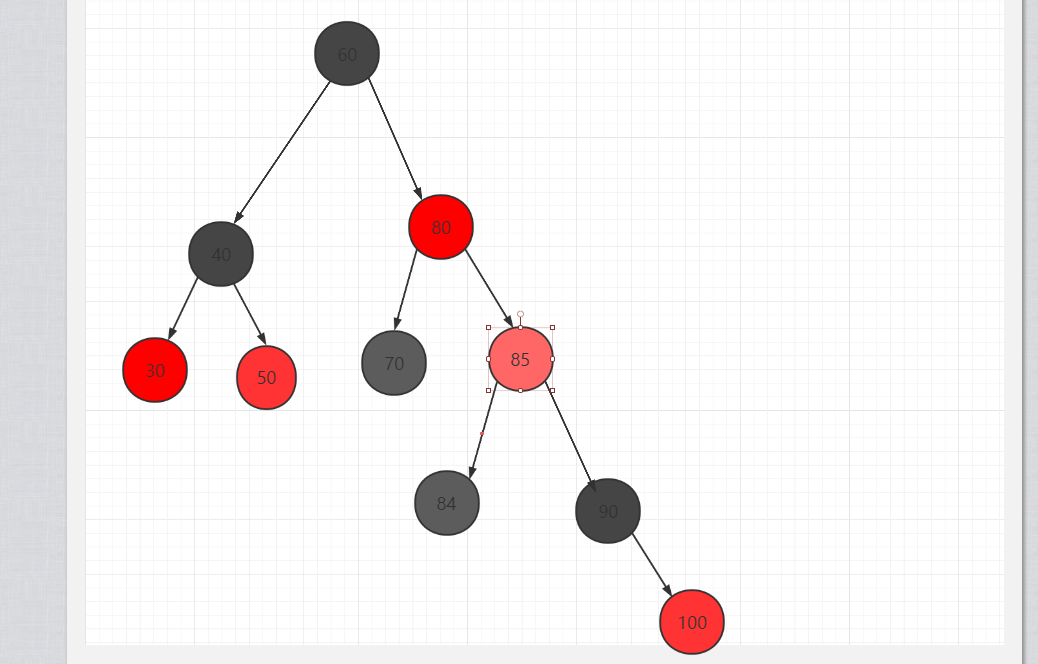
- 解决:根据上面的情况此时父节点跟叔父节点都是红色,满足情况二,进行变色,变色后是图2,但是此时又有问题,80跟85都为红色,违法红黑树相邻节点不能都为红色,此时85的父节点是红色,叔父节点为黑色,这就是情况三,遇到这种情况改着解决,其实跟情况一类似:旋转+变色
- 旋转+变色之后就是图3,注意这个时候是60围绕着80旋转,60变红色,80变黑色,原本80的子节点变为60的子节点
- 所以这种情况也是旋转+变色
图1:
图2:
图3
总结: 红黑树的变化大概就这几种情况,万变不离其中,但是要先了解什么是左旋,什么是右旋。