十三、并查集
并查集的作用:
- 可以回答连接问题。
- 判断网络中结点间的连接状态。
- 可以实现数学中的集合。
- 连接问题和路径问题。连接问题比路径问题回答的问题要少。
- 和二分查找法作比较。
- 和 select 作比较。
- 和堆作比较。
- 判断一个图中有没有环,可以用并查集作为辅助的数据结构。
优化策略:[数据压缩]和[按秩合并]
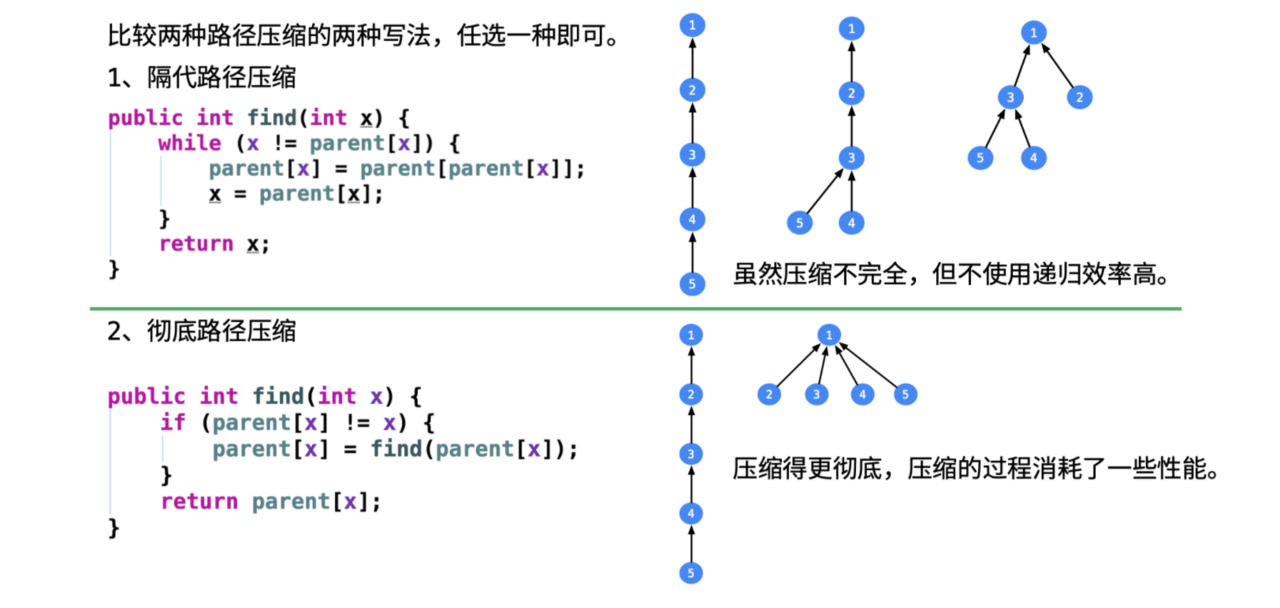
(一)数据压缩:隔代压缩与完全压缩
- 隔代压缩性能比较高,虽然压缩不完全,不过多次执行隔代压缩也能达到完全压缩的效果,通常大佬偏向于隔代压缩;
- 完全压缩需要借助系统栈,使用递归的写法。或者先找到当前结点的根结点,然后把沿途上所有的结点都指向根结点,得遍历两次。
(二)按秩合并
秩也有两种含义:
秩表示以当前结点为根结点的子树结点总数,即这里的「秩」表示 size 含义; 秩表示以当前结点为根结点的子树的高度,即这里的「秩」表示 rank 含义(更合理,因为查询时候的时间性能主要决定于树的高度)。 注:如果同时使用「路径压缩」与「按秩合并」,这里的「秩」就失去了它的定义,但即使秩表示的含义不准确,也能够作为合并时候很好的「参考」。在这种情况下,并查集的查询与合并的时间复杂度可以达到接近 O(1)。
990. 等式方程的可满足性[1]
class Solution {
public boolean equationsPossible(String[] equations) {
UnionFind unionFind=new UnionFind(26);
for(String equation:equations){
char[]charArray=equation.toCharArray();
if(charArray[1]=='='){ int index1=charArray[0]-'a'; int index2=charArray[3]-'a'; unionFind.union(index1,index2); } } for(String equation:equations){ char[]charArray=equation.toCharArray(); if(charArray[1]=='!'){ int index1=charArray[0]-'a'; int index2=charArray[3]-'a'; if(unionFind.isConnection(index1,index2)){ return false; } } } return true; } private class UnionFind{ private int []parent; //构造方法 public UnionFind(int n){ parent=new int [n]; for(int i=0;i<n;i++){ parent[i]=i; } } //查找 public int find(int x){ while(x!=parent[x]){ parent[x]=parent[parent[x]]; x=parent[x]; } return x; } //合并 public void union(int x,int y){ int rootX=find(x); int rootY=find(y); parent[rootX]=rootY; } //判断是否连接 public boolean isConnection(int x,int y){ return find(x)==find(y); } } }
684. 冗余连接[2]
class Solution {
public int[] findRedundantConnection(int[][] edges) {
int len=edges.length;
UnionFind unionFind=new UnionFind(len+1);
for(int[] edge:edges){
if(unionFind.isConnection(edge[0],edge[1])){ return edge; } unionFind.union(edge[0],edge[1]); } return new int[0]; } //并查集 private class UnionFind{ private int []parent; //构造方法 public UnionFind(int n){ parent=new int [n]; for(int i=0;i<n;i++){ parent[i]=i; } } //查找 public int find(int x){ while(x!=parent[x]){ parent[x]=parent[parent[x]]; x=parent[x]; } return x; } //合并 public void union(int x,int y){ int rootX=find(x); int rootY=find(y); parent[rootX]=rootY; } //判断是否连接 public boolean isConnection(int x,int y){ return find(x)==find(y); } } }
参考资料
[1]
990、 等式方程的可满足性: https://leetcode-cn.com/problems/satisfiability-of-equality-equations/
[2]
684、 冗余连接: https://leetcode-cn.com/problems/redundant-connection/