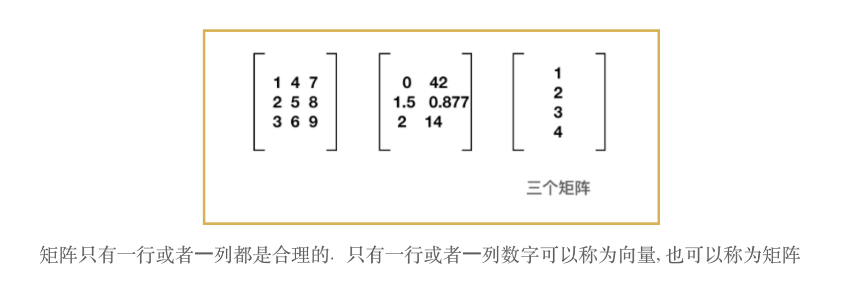
向量
什么是向量?
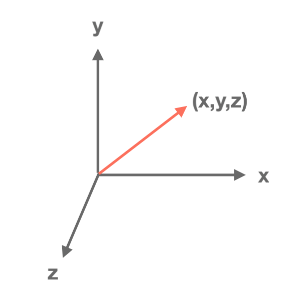
在OpenGL中,我们总是使用向量来表示带方向的量,例如在3D坐标系中,从原点到一个任意点(x,y,z)的一条带箭头的线段,它有两个重要的值:方向,数量(也可以理解为是长度).
标量只表示数量,大小
单位向量
长度为1的向量为单位向量
那么我们应该如何计算向量的长度呢?
但是如果一个向量并不是单位向量,也可以通过标准化的过程,将它缩放长度为1.
使用一个非零向量除以它的模(向量的长度),就可以得到方向相同的单位向量
(x/|xyz|, y/|xyz|, z/|xyz|)
定义向量
在OpenGL的math3d库中
- M3DVector3f表示一个三维向量(x,y,z)
- M3DVector4f表示一个四维向量(x,y,z,w),xyz通过除以w的值来进行缩放
参考
//三维向量/四维向量的声明
typedef float M3DVector3f[3];
typedef float M3DVector4f[4];
//声明⼀个三维向量M3DVector3f:类型vVector:变量名M3DVector3fvVector;
//声明⼀个四维向量并初始化⼀个四维向量
M3DVector4f vVertex = {0,0,1,1};
//声明⼀个三分量顶点数组,例如⽣成⼀个三⻆形
//M3DVector3f vVerts[]={
-0.5f,0.0f,0.0f,
0.5f,0.0f,0.0f,
0.0f,0.5f,0.0f};
向量可以做什么?
点乘
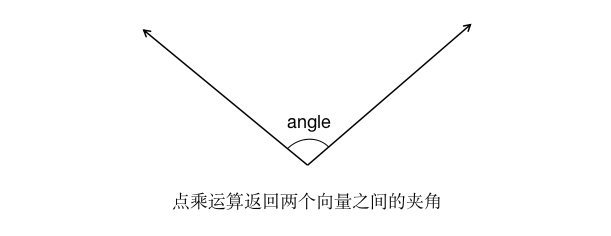
当需要计算出,两个三维向量(单位向量)之间的夹角时,这样的运算过程称为点乘.结果会返回一个[=1,1]范围的值,这个值就是这两个单位向量之间夹角的cos值(余弦值).
在math3d库中,包含了这样的函数来进行计算点乘
- float m3dDotProduct3(const M3DVector3f u,const M3DVector3f v); // 获得两个单位向量之间的点乘结果
- float m3dGetAngleBetweenVector3(const M3DVector3f u,const
M3DVector3f v); // 更高级的函数,直接返回夹角的弧度值
叉乘
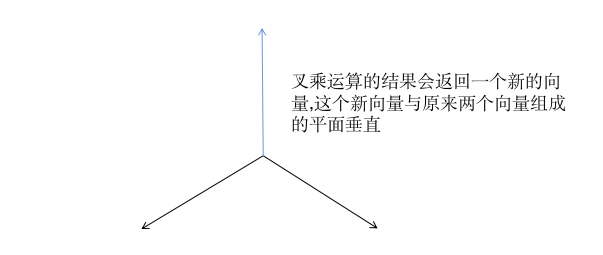
当需要获得,垂直于两个向量定义的平面的向量时,这样的运算过程称为叉乘,结果会返回一个新的向量,新的向量会垂直于原来两个向量定义的平面.
math3d库中,计算叉乘的函数
void m3dCrossProduct3(M3DVector3f result,constM3D Vector3f u,const M3DVector3f v);
注意!!!
- 运算叉乘的两个向量不必是单位向量
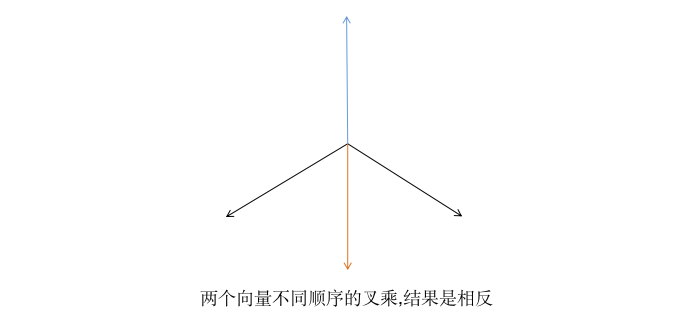
- 计算的顺序不同,结果也是不同
V1 叉乘 V2 — V2 叉乘 V1,它们的结果都会是垂直与V1,V2组成的平面,但是结果是指向相反方向的向量.
矩阵
如果在空间中有一个点,将它围绕任意位置沿任意方向旋转一定角度后,这个点新的位置,需要通过矩阵来计算,而不再是之前对顶点x,y,z进行简单的加减操作就可以的.因为新的位置的x,不仅与原来的x坐标和其他旋转参数有关,还会和y、z的坐标值有关.
在上边定义向量的参考代码里,我们看到OpenGL中,更多倾向使用一维数组来定义,这样做的原因在于OpenGL使用的是列优先矩阵排序的约定
单位矩阵
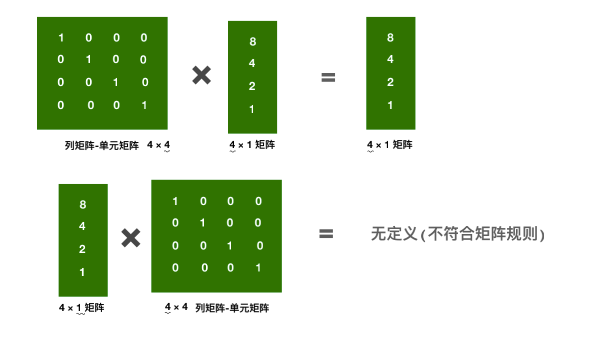
将一个向量乘以一个单元矩阵,就相当于用这个向量乘以1,不会发生任何改变.
- 主对角线上的数据都为1
- 向量 * 单元矩阵 == 向量 * 1
- 与矩阵相乘的前提,列数 = 矩阵的行数,否则不符合矩阵的规则
矩阵相乘
- 从线性代数角度
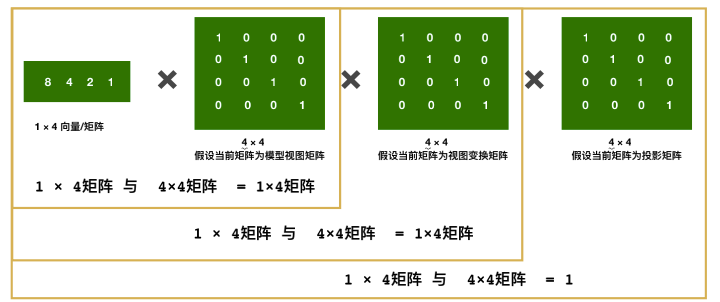
在线性代数的维度,为了便于书写,所以坐标计算,都是从左向右顺序,进行计算,如下:
变换后的顶点向量 = V_local * M_model * M_view * M_pro;
变换后的顶点向量 = 顶点 * 模型矩阵 * 视图矩阵 * 投影矩阵;
由于顶点向量是行向量,要满足与矩阵相乘的规则,需要将矩阵放在右边,属于右乘.
- 从OpenGL角度
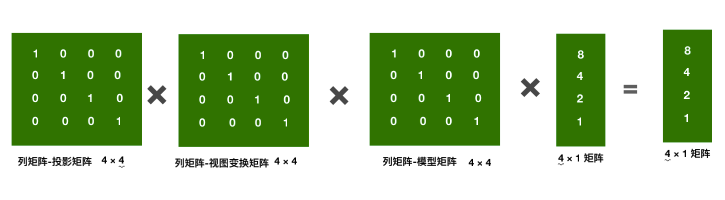
在OpenGL中,矩阵规定为列优先,所以顶点以列向量的方式表示,同一计算方式就会有所改变,如下:
变换后的顶点向量 = M_pro * M_view * M_model * V_local;
变换后的顶点向量 = 投影矩阵 * 视图矩阵 * 模型矩阵 * 顶点;
这样的情况下,属于左乘
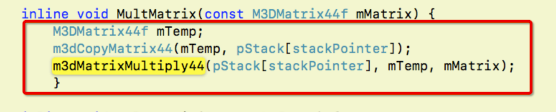
- 从矩阵栈中矩阵相乘的源码分析
1.首先将栈顶的矩阵保存在mTemp
2.栈顶矩阵mTemp * 传入的mMatrix //左乘
3.结果保存在栈顶