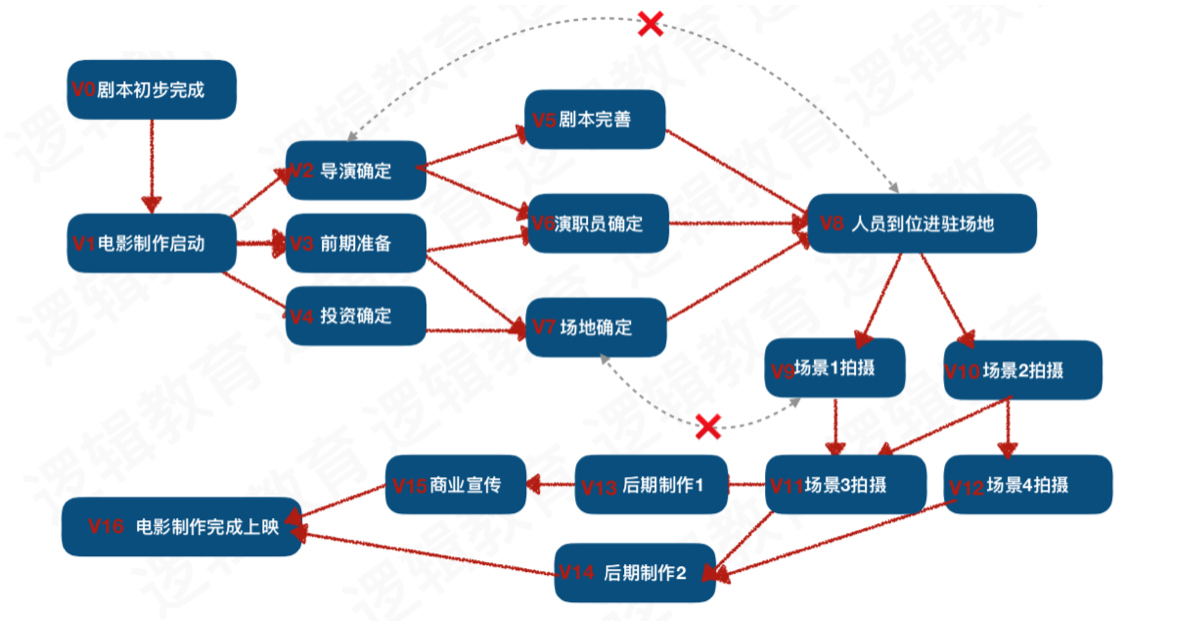
AOV网
在一个表示⼯工程的有向图中, ⽤用顶点表示活动, ⽤用弧表示活动之间的优先关系,这样 有向图为顶点表示活动的⽹网. 我们称为AOV⽹网(Activity On Vertex Network).
- AOV图中的弧表示活动之间存在的某种制约关系
- AOV图中不能存在回路
拓扑排序
对一个有向图构造拓扑序列的过程,就叫拓扑排序。
基本思路:
从AOV网选择一个入度为0的顶点输出,然后删除此顶点,并且删除以此顶点指出去的弧,继续重复此步骤,直到输出全部顶点,或者AOV网中不存在入度为0的顶点为止。
入度:指向当前顶点的顶点个数。例如上图V0就是入度为0的顶点
代码实现
因为涉及到顶点的删除操作,这里使用邻接表实现会更方便
基本数据结构
/* Status是函数的类型,其值是函数结果状态代码,如OK等 */
typedef int Status;
/*邻接矩阵结构 */
typedef struct
{
int vexs[MAXVEX];
int arc[MAXVEX][MAXVEX];
int numVertexes, numEdges;
}MGraph;
/* 邻接表结构****************** */
//边表结点
typedef struct EdgeNode
{
//邻接点域,存储该顶点对应的下标
int adjvex;
//用于存储权值,对于非网图可以不需要
int weight;
//链域,指向下一个邻接点
struct EdgeNode *next;
}EdgeNode;
//顶点表结点
typedef struct VertexNode
{
//顶点入度
int in;
//顶点域,存储顶点信息
int data;
//边表头指针
EdgeNode *firstedge;
}VertexNode, AdjList[MAXVEX];
//图结构
typedef struct
{
AdjList adjList;
//图中当前顶点数和边数
int numVertexes,numEdges;
}graphAdjList,*GraphAdjList;
拓扑排序实现
Status TopologicalSort(GraphAdjList GL){
EdgeNode *e;
int i,k,gettop;
int top = 0; // 栈顶的下标
int count = 0; // 用于统计输出顶点的个数
// 初始化一个栈用来存储入度为0的顶点
int *stack = (int *)malloc(sizeof(int)*GL->numVertexes);
// 1.遍历邻接表顶点表,将入度为0的顶点入栈
for (i = 0; i<GL->numVertexes; i++) {
if (GL->adjList[i].in == 0) {
stack[++top] = i; //将入度为0的顶点入栈
}
}
printf("top = %d\n",top);
//2.循环栈顶元素
while (top != 0) {
// 出栈
gettop = stack[top--];
printf("%d -> ",GL->adjList[gettop].data); // 输出顶点
count++; // 计数,用来最终计算图中的顶点是否全部输出
// 遍历与出栈的顶点对应的弧链表
for (e = GL->adjList[gettop].firstedge; e; e = e->next) {
// 获取与出栈顶点有关联的顶点
k = e->adjvex;
// 之前的栈顶顶点已经出栈,所以与之有关联的顶点的入度进行减1操作,
// 减1后如果入度为0,同样需要入栈
if (!(--GL->adjList[k].in)) {
stack[++top] = k;
}
}
}
printf("\n");
if (count < GL->numVertexes) {
return ERROR;
}
return OK;
}