1. 深度优先遍历
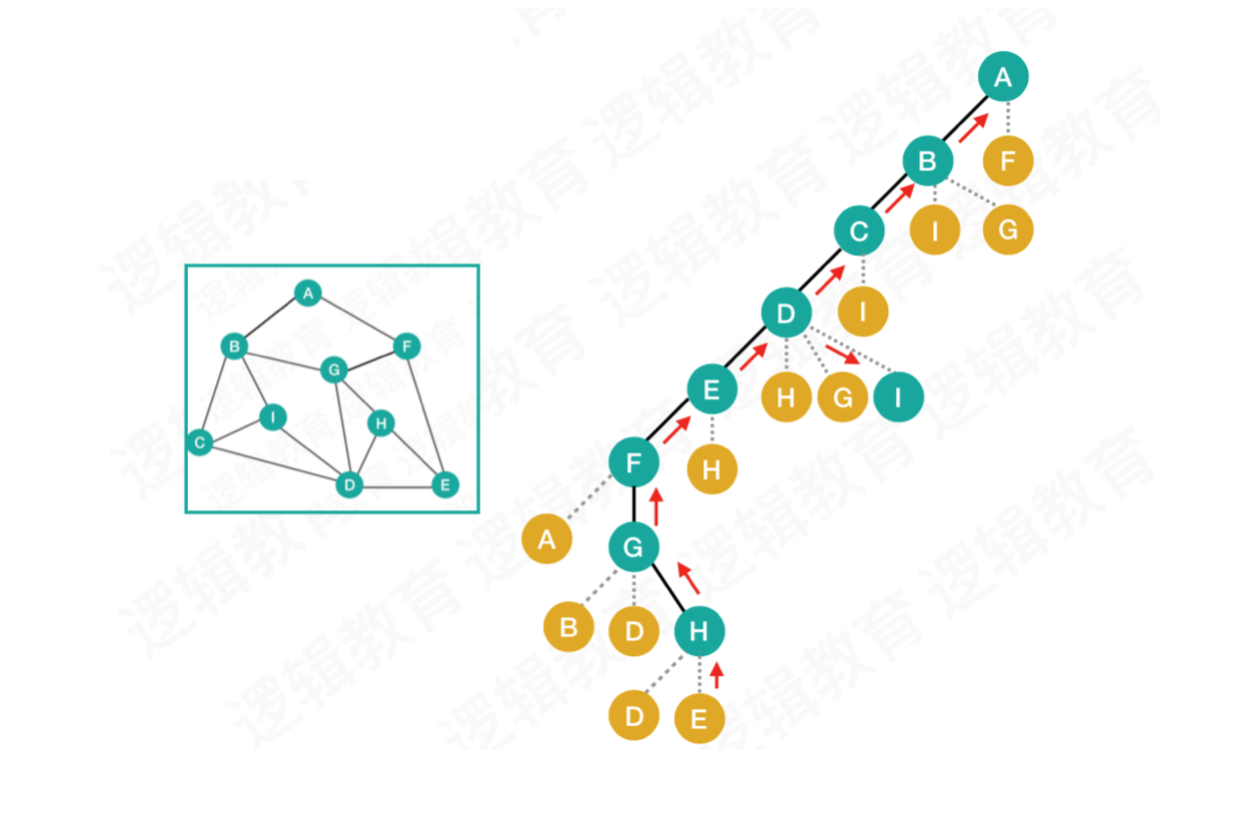
深度优先遍历也称为,深度优先搜索,简称为DFS。会先从一个顶点开始,找到其未被访问的邻接点出发,直至所有的顶点都被访问,其实深度优先是一个递归的过程。
- 邻接矩阵的深度优先遍历
实现思路:
1、 将图的顶点和边信息保存在图结构中
2、 创建一个visited数组,用来标识顶点是否被遍历过
3、 初始化visited数组,将数组元素置为FALSE
4、 选择任意顶点开始遍历
5、 进入递归,visited中标记该顶点为已遍历
6、 循环遍历边表,判断当前arc[i][j]是否等于1,并且当前顶点没有被遍历过,继续进行递归
// DFS遍历
Boolean visited[MAXVEX]; // 访问标志的数组 ,用来记录顶点是否被访问过
/**
1.标识顶点是否被标记过
2.选择从某一个顶点开始(非连通图的情况)
3.进入递归,打印i点信息
4.[i][j]是否为1,
*/
void DFS(MGraph G,int i){
//首先把顶点的标记已经访问
visited[i] = TRUE;
printf("%c",G.vexs[i]);
//从0到所有的节点 遍历看是否与当前节点是否有关系
for (int j = 0; j<G.numVertexes; j++) {
/*
G.arc[i][j] == 1 与当前节点存在连接关系
是否已经被访问
*/
if (G.arc[i][j] == 1 && !visited[j]) {
DFS(G, j); // 对访问的邻接顶点递归调用
}
}
}
// 邻接矩阵的深度遍历操作
void DFSTravese(MGraph G){
//1.初始化 开始遍历时所有顶点的标记都为FALSE
for (int i = 0; i<G.numVertexes; i++) {
visited[i] = FALSE;
}
// for循环可以保证在非连通图的情况下,所有的顶点也能遍历到
for (int i = 0; i<G.numVertexes; i++) {
// 没有访问 才可以进行深度遍历
if (!visited[i]) {
DFS(G, i);
}
}
}
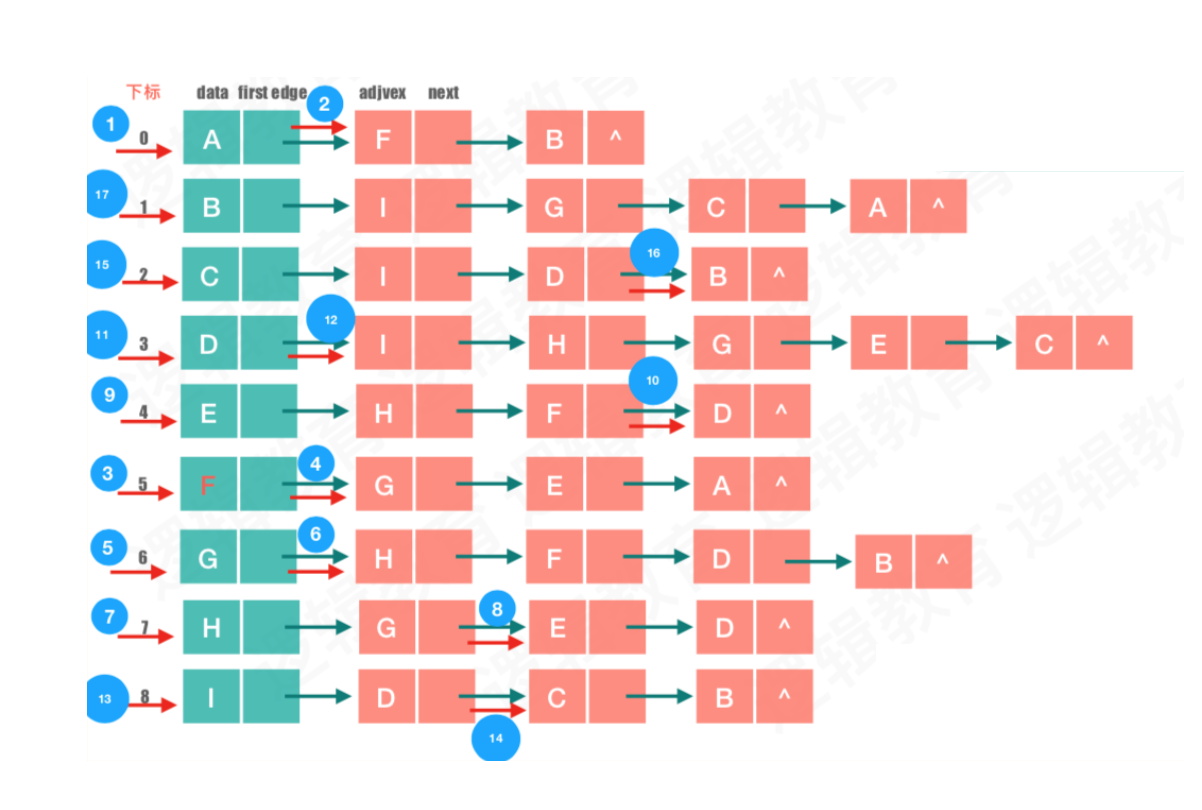
- 邻接表的深度优先遍历
实现思路:
1、 利利⽤用邻接矩阵将信息存储到邻接表中
2、 创建⼀一个visited 数组,⽤来标识顶点是否已经被遍历过.
3、 初始化visited 数组,将数组中元素置为FALSE
4、 选择顶点开始遍历.(注意⾮非连通图的情况)
5、 进⼊入递归; 打印i 对应的顶点信息. 并将该顶点标识为已遍历.
6、 循环遍历边表,判断当前顶点 是否等于1,并且当前该顶点没有被遍历过,则继续递归 DFS;
Boolean visited[MAXSIZE]; /* 访问标志的数组 */
/* 邻接表的深度优先递归算法 */
void DFS(GraphAdjList GL, int i){
EdgeNode *p;
visited[i] = TRUE;
//打印顶点数据
printf("%c ",GL->adjList[i].data);
p = GL->adjList[i].firstedge;
while (p) {
// 判断p的adjvex对应的顶点表的下标
if (!visited[p->adjvex]) {
DFS(GL, p->adjvex); // 找到未被访问的顶点,继续递归遍历
}
p = p->next; // 如果被访问的话,找到下一个
}
}
/* 邻接表的深度遍历操作 */
void DFSTraverse(GraphAdjList GL)
{
//1. 将访问记录数组默认置为FALSE
for (int i = 0; i < GL->numVertexes; i++) {
/*初始化所有顶点状态都是未访问过的状态*/
visited[i] = FALSE;
}
//2. 选择一个顶点开始DFS遍历. 例如A
for(int i = 0; i < GL->numVertexes; i++)
//对未访问过的顶点调用DFS, 若是连通图则只会执行一次.
if(!visited[i])
DFS(GL, i);
}
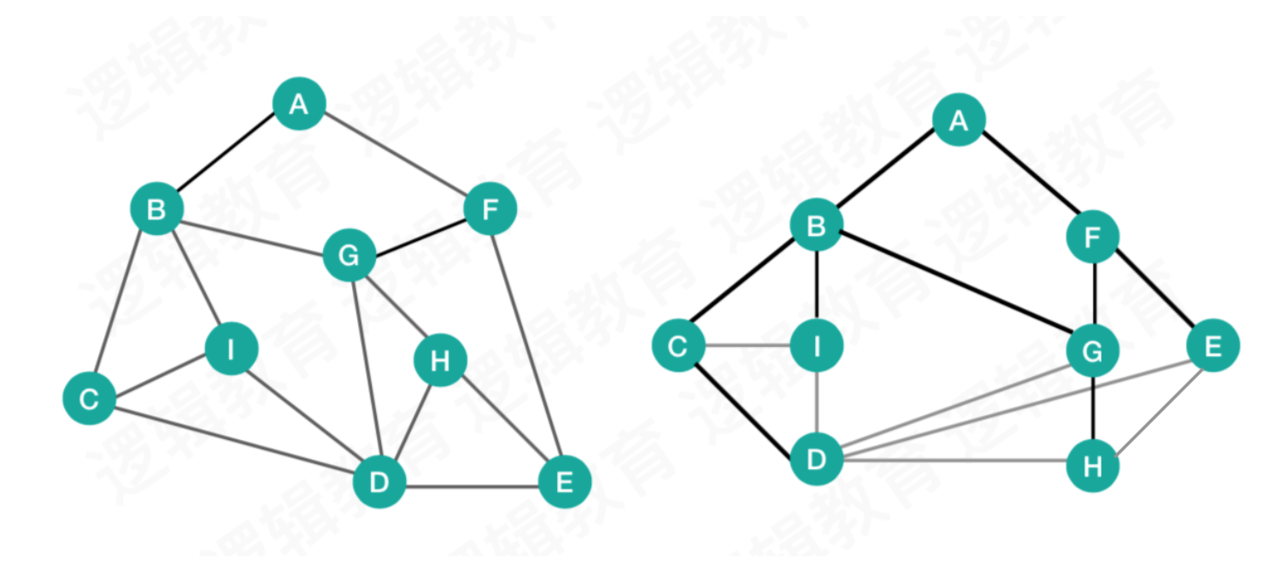
2. 广度优先遍历
广度优先遍历又称为广度优先搜索,简称BFS。
如果说图的深度优先遍历类似树的前序遍历,那么图的广度优先遍历就类似于树的层序遍历。稍稍变形如下。
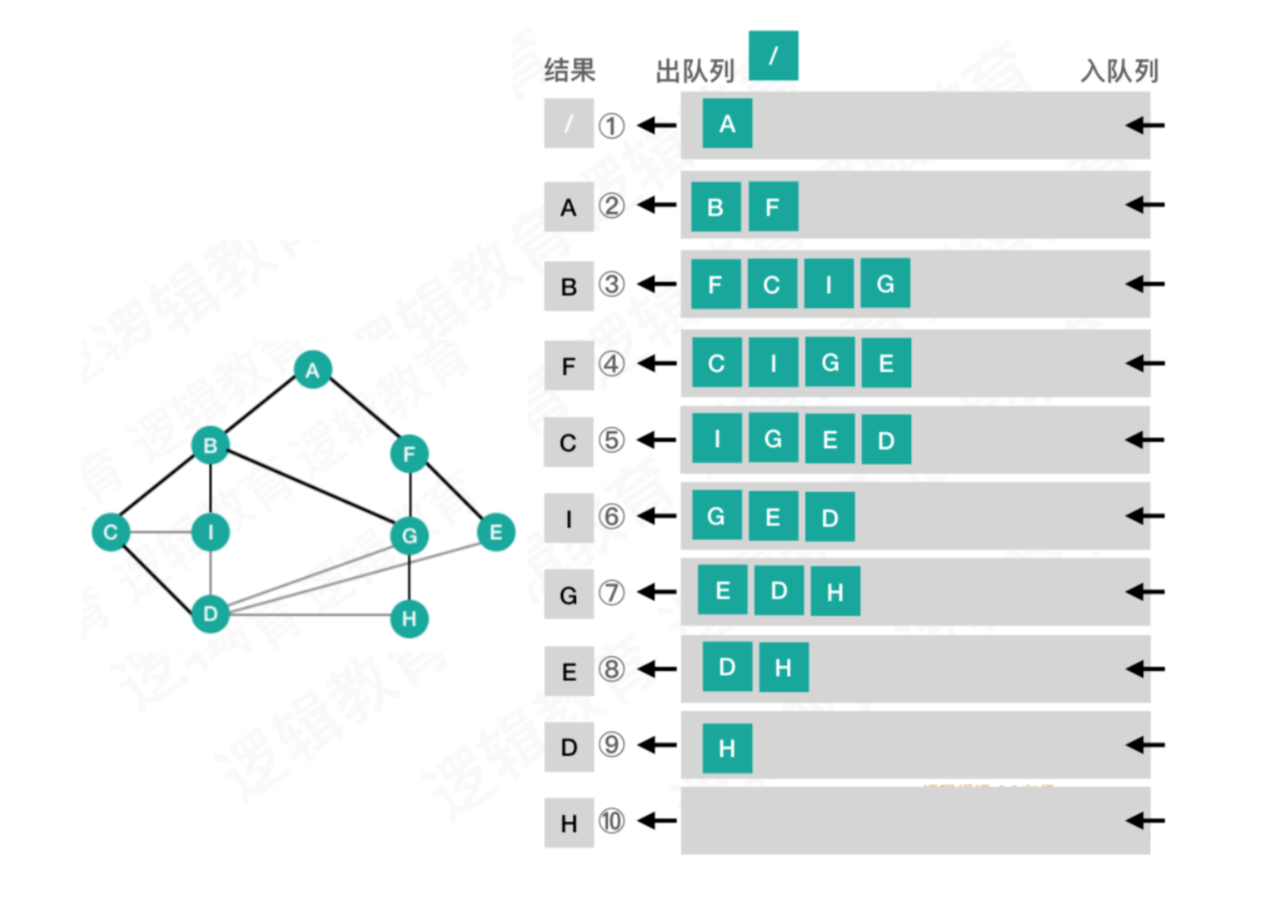
广度优先遍历的实现:
1、 把根节点放到队列列的末尾。
2、 每次从队列列的头部取出⼀一个元素,查看这个元素所有的下⼀一级元素,把它们放到队列的末尾,并把这个元素记为下一级元素的前驱
3、 找到所要找的元素时结束程序。
4、 如果遍历整个树还没有找到,结束程序.
- 邻接矩阵的广度优先遍历
Boolean visited[MAXVEX]; /* 访问标志的数组 */
void BFSTraverse(MGraph G){
Queue Q;
InitQueue(&Q);
//将访问标识数组置为未访问状态
for (int i = 0 ; i < G.numVertexes; i++) {
visited[i] = FALSE;
}
// 遍历所有的顶点,这个循环是针对非连通图,对于连通图只会执行1次
for (int i = 0; i<G.numVertexes; i++) {
if (!visited[i]) {
visited[i] = TRUE;
printf("%c ",G.vexs[i]);
// 入队
EnQueue(&Q, i);
while (!QueueEmpty(Q)) {
// 出队
DeQueue(&Q, &i);
for (int j = 0; j<G.numVertexes; j++) {
// 找到下一级别的顶点,将其入栈
if (G.arc[i][j] == 1 && !visited[j]) {
visited[j] = TRUE;
printf("%c ",G.vexs[j]);
EnQueue(&Q, j);
}
}
}
}
}
}
- 邻接表的广度优先遍历
Boolean visited[MAXSIZE];
void BFSTraverse(GraphAdjList GL){
// 创建结点
EdgeNode *p;
Queue Q;
InitQueue(&Q);
// 将访问标识数组置为未访问状态
for(int i = 0; i < GL->numVertexes; i++){
visited[i] = FALSE;
}
// 遍历所有的顶点,这个循环是针对非连通图,对于连通图只会执行1次
for (int i = 0; i<GL->numVertexes; i++) {
if (!visited[i]) {
visited[i] = TRUE;
printf("%c ",GL->adjList[i].data);
//入队
EnQueue(&Q, i);
while (!QueueEmpty(Q)) {
//出队
DeQueue(&Q, i);
p = GL->adjList[i].firstedge;
while (p) {
if (!visited[p->adjvex]) {
visited[p->adjvex] = TRUE;
printf("%c ",GL->adjList[p->adjvex].data);
EnQueue(&Q, p->adjvex);
}
p = p->next;
}
}
}
}
}