1.队列的定义
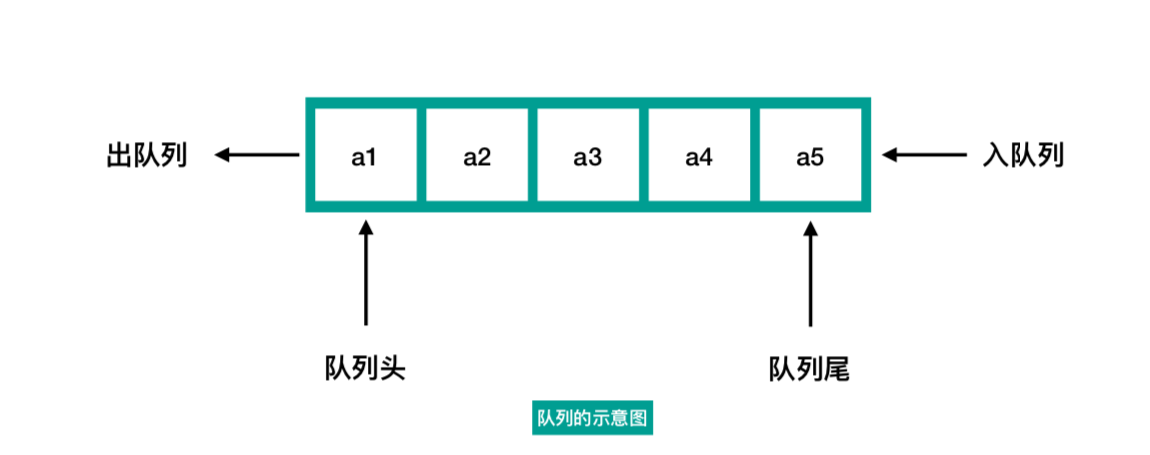
队列(queue)是只允许在一端(队尾)进行插入操作,在另一端(队头)进行删除操作的线性表。遵循先进先出。
2.顺序存储队列的问题
2、1 时间复杂度
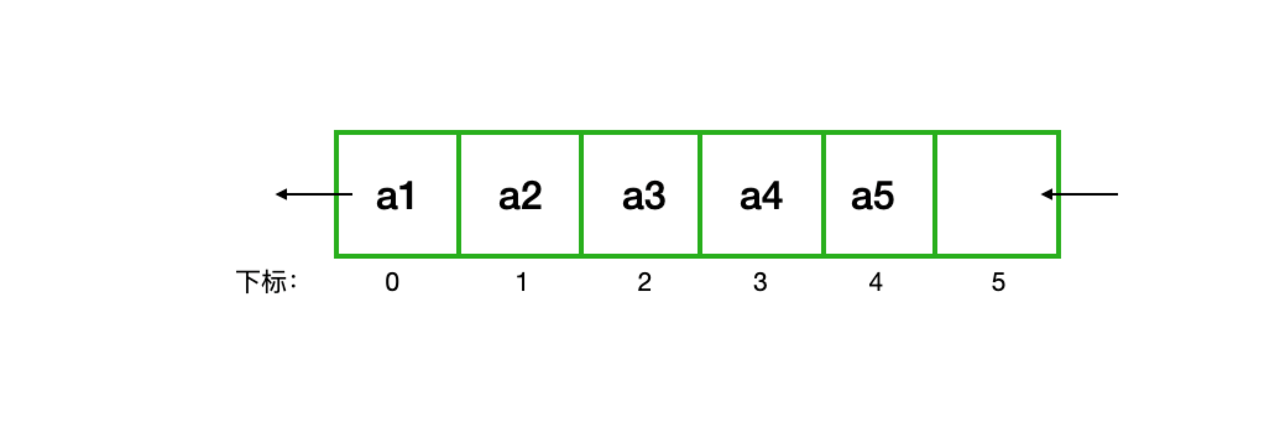
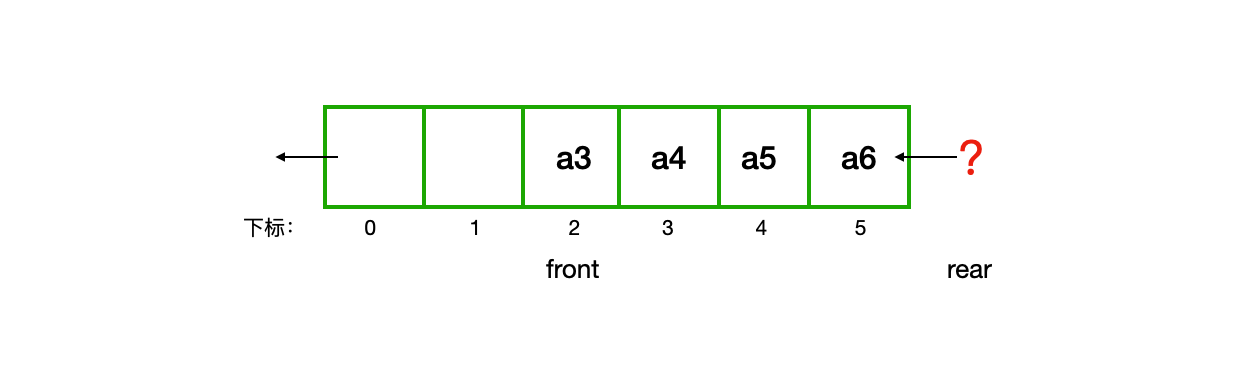
假设一个队列,当我们往队列中添加数据时,即在下标5的位置追加一个元素a6,不用移动任何元素,时间复杂度为O(1),
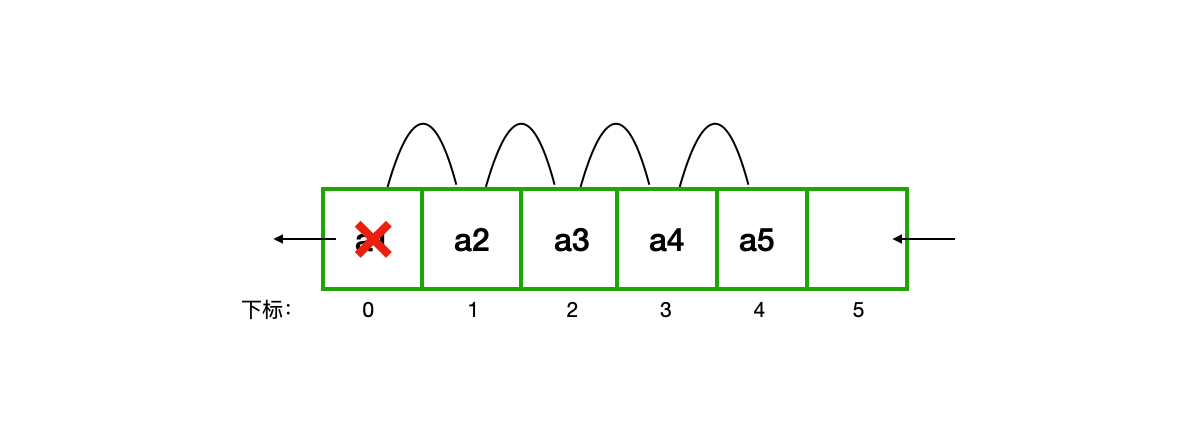
那么当我们从队列中删除数据时,即在队头删除元素a1,需要将后续元素向前移动,以保证队列的队头还在下标为0的位置,那么它的时间复杂度就是O(n),则出队的性能就会大大增加。
2、2、假溢出
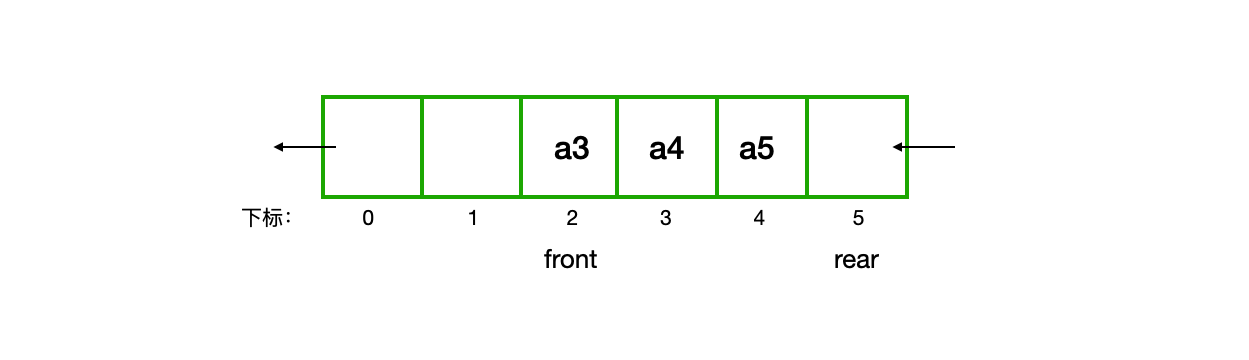
为避免出队的问题,不再以下标为0固定为队头,引入了两个指针,front指针指向队头元素,rear指针指向队尾元素的下一个位置,当front等于rear时,队列为空。
但是这样又出现了新的问题:
- 当队列进进出出数据后,front指针指向了队列后边的元素,而插入数据总是从队尾添加,这样会导致front指针前的空间空置着。
- 当插入的数据大于了队列的MAXSIZE,rear指针再往后加,就会导致越界的错误,但实际上,队列的0,1位置还是空闲的。我们称这种现象为”假溢出”。
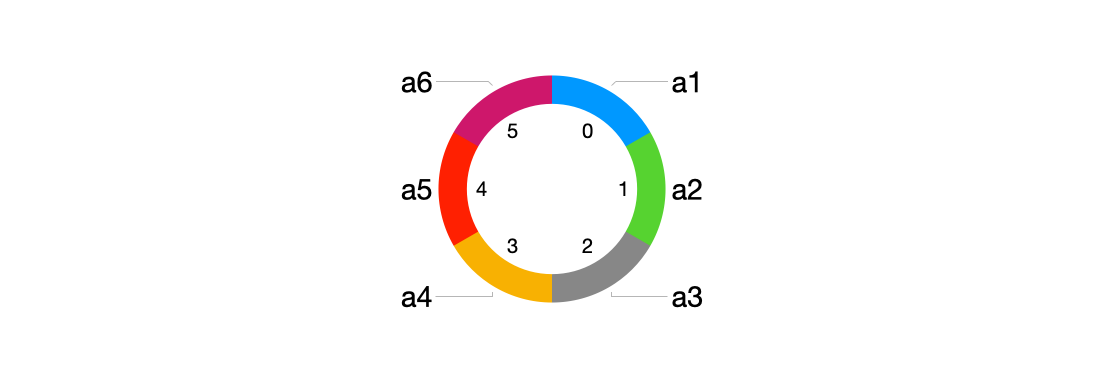
3.循环队列
解决假溢出的办法就是,当队列后边满了之后,将rear指针再从头开始头尾相接,这样的顺序存储结构的队列称为循环队列。
新的问题又出现了…
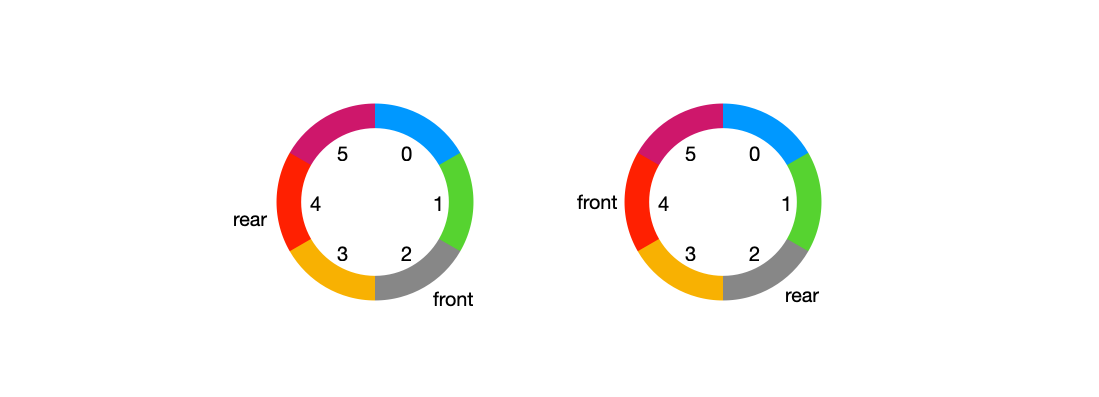
上边我们提到, 当front等于rear时,队列为空。 那么当队列满时,也是front等于rear,这要如何判断队列是空的还是满的?
- 一:设置一个标志变量flag,当front==rear,且flag=0时,队列为空,当front==rear,flag=1时,队列为满。
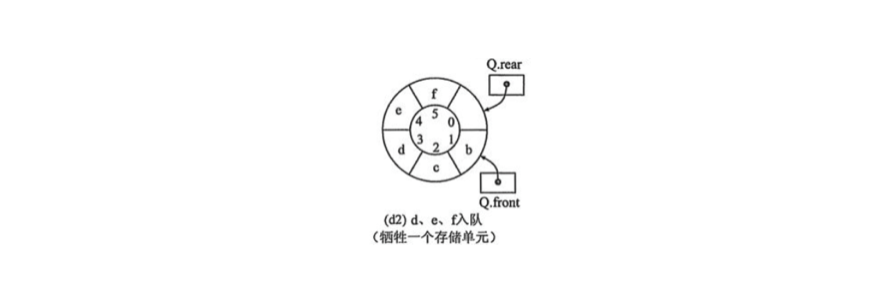
- 二:队列为空时,front==rear,当队列满时,保留一个空闲单元。即
(rear+1)%MAXSIZE == front。需要用取模运算,因为不停rear加1可能会超过一圈。这里我们主要使用第二种方法来实现循环队列。
4.顺序存储结构实现循环队列
4、1 结构体
typedef struct {
SElemType data[MAXSIZE];
int front; // 队列头
int rear; // 队列尾
}SqQueue;
4、2 初始化空队列
Status InitQueue(SqQueue *S){
S->front = 0;
S->rear = 0;
return OK;
}
4、3 添加操作
Status EnterQueue(SqQueue *S,SElemType e){
if (S == NULL) {
return ERROR;
}
if ((S->rear+1)%MAXSIZE == S->front) {
printf("队列已满\n");
return ERROR;
}
S->data[S->rear] = e;
S->rear = (S->rear+1)%MAXSIZE; // 防止rear值大于一圈
return OK;
}
4、4 删除操作
Status DeleteQueue(SqQueue *S,SElemType *e){
if (S == NULL) {
return ERROR;
}
if (S->front == S->rear) {
printf("队列已空\n");
return ERROR;
}
*e = S->data[S->front];
S->front = (S->front+1)%MAXSIZE;
return OK;
}
4、5 队列长度计算
- 当rear>front时,队列的长度为rear-front;
- 当rear<front时,队列的长度为MAXSIZE-front 与 rear的和。
通用的计算长度公式为:
(rear – front + MAXSIZE)%MAXSIZE
int GetQueueLength(SqQueue S){
return (S.rear - S.front + MAXSIZE) % MAXSIZE;
}
4、6 判断是否为空
Status QueueEmpty(SqQueue S){
if (S.front == S.rear) {
return TRUE;
}
return FALSE;
}
4、7 遍历队列
Status QueueTraver(SqQueue S){
int p = S.front;
while (p+1 != S.rear+1) {
printf("%d ",S.data[p]);
p = (p+1)%MAXSIZE;
}
printf("\n");
return OK;
}