1. 双向链表
双向链表(double linked list)是在单链表的每个结点中,再设置一个指向前驱结点的指针域。所以在双向链表中的结点都有两个指针域,一个指向直接后继,另一个指向直接前驱。

在单链表中,使用next指针,使得我们要查找下一结点的时间复杂度为O(1),可是如果要查找的是上一个结点的话,那么时间复杂度就是O(n)了,因为每次都要从头开始遍历查找。为了克服这个缺点,设计了双向链表–用空间换时间。
- 定义结点
//定义结点
typedef struct Node{
ElemType data; // 结点数据域
struct Node *prior; // 结点前指针域
struct Node *next; // 结点后指针域
}Node;
我们把链表中第一个结点的存储位置叫做头指针,第一个结点称为首元结点,但是为了我们更加方便的对链表进行增删改查的操作,会在第一个结点前附设一个结点,称为头结点。
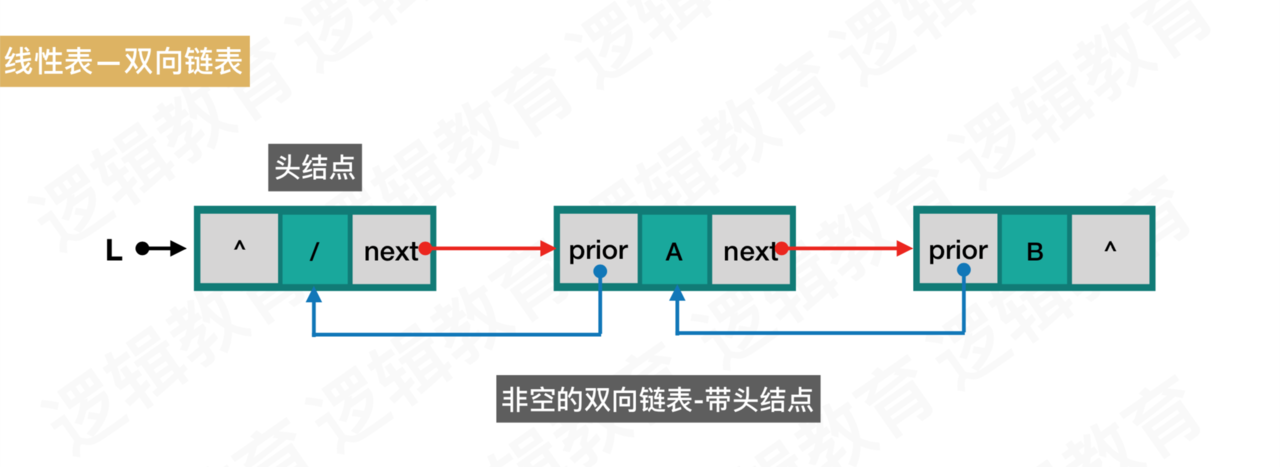
头结点的数据域可以不存储任何信息,也可以存储一些与链表有关的信息,头结点的prior为空,头结点的next指针域指向首元结点的指针,首元结点的prior指针指向头结点,首元结点的next指向下一个结点,假如没有的话,next为空,如下图:
- 创建
1、 新建一个头结点
2、 遍历创建链表结点,设置它的prior,next指针
// 创建双向链接
Status createLinkList(LinkList *L){
//*L 指向头结点
*L = (LinkList)malloc(sizeof(Node)); // 创建一个头结点,*L指向它
if (*L == NULL) return ERROR;
(*L)->prior = NULL; // 指针域先置空,数据域-1
(*L)->next = NULL;
(*L)->data = -1;
LinkList p = *L; // 结点变量, 第一次赋值为头结点
for(int i=0; i < 10;i++){
//1.创建新结点
LinkList temp = (LinkList)malloc(sizeof(Node));
temp->prior = NULL;
temp->next = NULL;
temp->data = i;
//2.为新增的结点建立双向链表关系
//① temp 是p的后继
p->next = temp;
//② temp 的前驱是p
temp->prior = p;
//③ p 要记录最后的结点的位置,方便下一次插入
p = p->next; // 也可以写做 p = temp;
}
return OK;
}
- 输出打印链表
Status showLinkList(LinkList L){
// 先把头结点过掉
LinkList temp = L->next;
if (temp == NULL) {
return ERROR;
}
while (temp) {
printf("%d ",temp->data);
temp = temp->next; // 打印后,temp记录到下一个结点,为空则是最后的结点
}
printf("\n");
return OK;
}
- 插入
1、 新建一个结点,初始化它的值
2、 找到要插入位置的前结点,这里要注意判断是否是空
3、 判断是否是最后一个结点,是的话只需要调整最后结点的next和新结点的prior指针域,否则需要依照先调整新结点与后结点的关系,再调整新结点与前结点的关系,防止结点丢失
// 插入
Status InsertLinkList(LinkList *L, int index, ElemType data){
if (index<1) { // 1.插入位置不合法
return ERROR;
}
// 2.新建要插入的节点
LinkList temp = (LinkList)malloc(sizeof(Node));
temp->data = data;
temp->prior = NULL;
temp->next = NULL;
LinkList p = *L; // 3.从头开始找
// 4.找到到要插入的位置的前节点
for (int i = 1; i<index && p; i++) { // 当i等于index时,此时的p则为插入位置的节点
p = p->next; //!!此处注意,当p是最后一个节点时,还会进到循环体,则此时的p是空的
}
// 5.由上,此处需要判断p是否是空的
if (p == NULL) {
return ERROR;
}
// 6.是否是最后一个节点
if (p->next == NULL) {
p->next = temp;
temp->prior = p;
}else{
// 先处理新节点与插入位置后结点之间的关系
p->next->prior = temp; // 1.插入位置结点的下一个节点的prior = 新节点
temp->next = p->next; // 2.新节点的next = 插入位置结点的next
// 再处理新节点与插入位置前结点之间的关系
p->next = temp; // 3.插入位置的节点的next = 新节点
temp->prior = p; // 4.新节点的prior = 插入位置的节点
}
return OK;
}
图解:
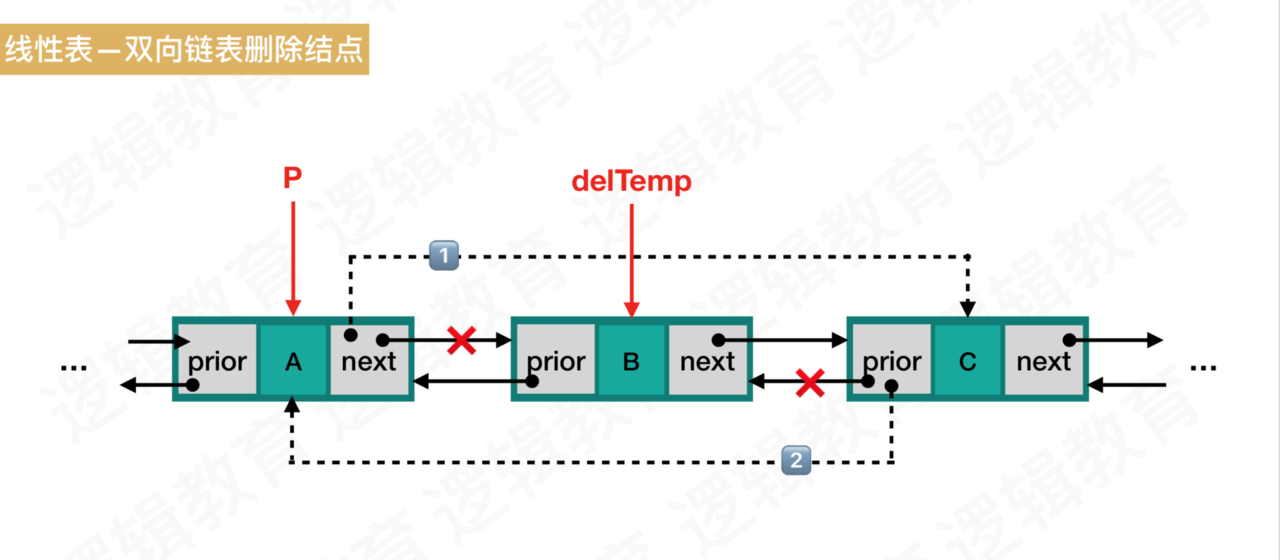
- 删除
1、 找到要删除位置的前一个结点
2、 调整删除位置前结点的next指针域
3、 判断是否删除的位置是在中间,是的话调整删除后结点的prior指针域
4、 置空释放要删除的结点空间
// 删除指定位置
Status DeleteLinkList(LinkList *L,int index,ElemType *e){
if (*L == NULL) {
return ERROR;
}
int k = 1; // 删除位置的计数
LinkList temp = *L;
// 找到要删除位置的前一个节点
for (k = 1; k<index && temp != NULL; k++) {
temp = temp->next;
}
//
if (temp == NULL) {
return ERROR;
}
// 将要删除的节点 并且将节点数据通过e传给main函数
LinkList deleTemp = temp->next;
*e = deleTemp->data;
temp->next = deleTemp->next; // 不用判断deleTemp是否是最后一个 它的->next 是否为空都无所谓
// 判断要删除的节点 是不是最后一个节点 不是的话将它的下一个节点的prior赋值temp
if (deleTemp->next != NULL) {
deleTemp->next->prior = temp;
}
// 删除节点 释放它的空间给内存
free(deleTemp);
return OK;
}
图解:
- 查找
// 查找链表是否存在某数据 返回数据位置
int FindLinkList(LinkList L, ElemType value){
// 过掉头结点
LinkList temp = L->next;
int i = 1;
while (temp) {
if (temp->data == value) {
return i;
}
i++;
temp = temp->next;
}
return -1;
}
- 更新结点数据
//
Status UpdateData(LinkList *L,int index,ElemType value){
if (*L == NULL) {
return ERROR;
}
LinkList temp = (*L)->next;
for (int i = 1; i<index&&temp; i++) {
temp = temp->next;
}
// 查询的结点不存在
if (temp == NULL){
return ERROR;
}
temp->data = value;
return OK;
}
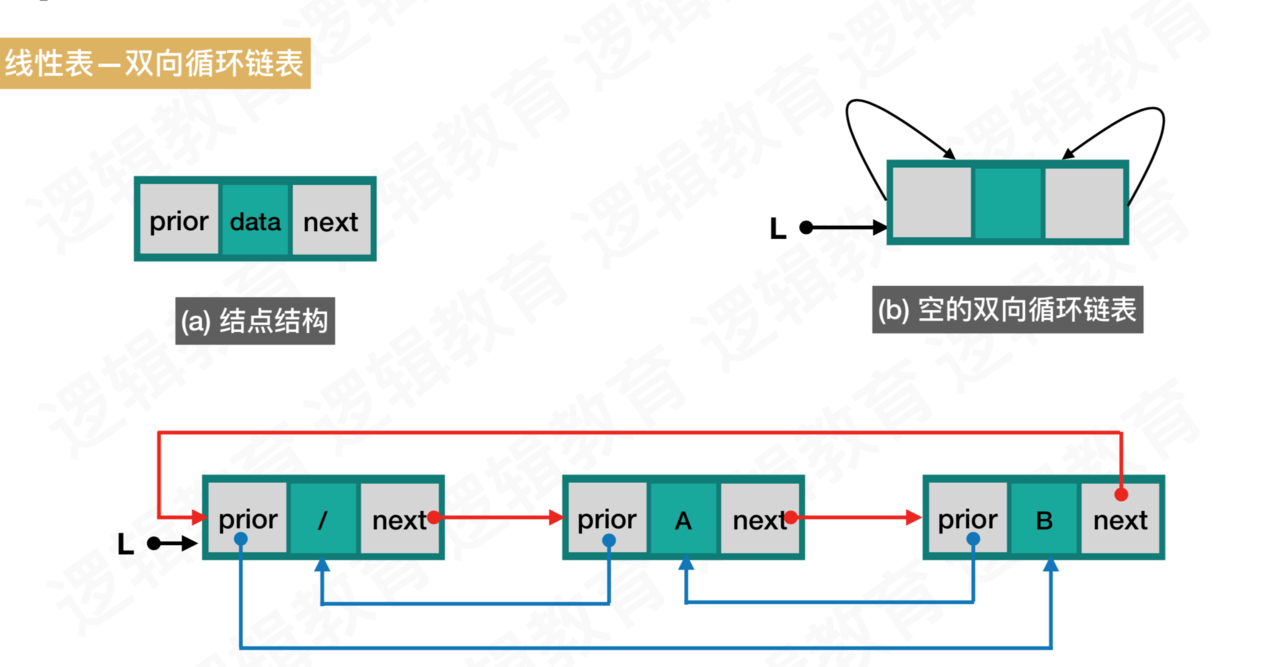
2.双向循环链表
将双向链表的最后一个结点的next指向头结点,头结点的prior指向最后一个结点,整个链表构成一个环,就构成了双向循环链表。
对于一个双向循环链表,p->next->prior = p = p->prior->next;指向的都是本身
- 创建
// 创建双向循环链表
Status createLinkList(LinkList *L){
// 头结点
*L = (LinkList)malloc(sizeof(Node));
if (*L == NULL) {
return ERROR;
}
// 初始化头结点的prior next为本身
(*L)->data = -1;
(*L)->prior = (*L);
(*L)->next = (*L);
LinkList temp = *L;
for (int i = 1; i<=1; i++) {
// 新结点
LinkList p = (LinkList)malloc(sizeof(Node));
p->data = i;
p->prior = NULL;
p->next = NULL;
// 为新增的结点简历双向链表关系
// 1.前结点的next指向新结点
temp->next = p;
// 2.新结点的prior指向前结点
p->prior = temp; // 3.新结点的next指向头结点
p->next = (*L);
// 4.头结点的prior指向新结点
(*L)->prior = p;
// 改变记录最后的结点的位置
temp = p; // 或者temp=temp->next;
}
return OK;
}
- 输出打印
Status showLinkList(LinkList L){
if (L == NULL) {
return ERROR;
}
LinkList temp = L->next;
while (temp && temp != L) {
printf("%d ",temp->data);
temp = temp->next;
}
printf("\n");
return OK;
}
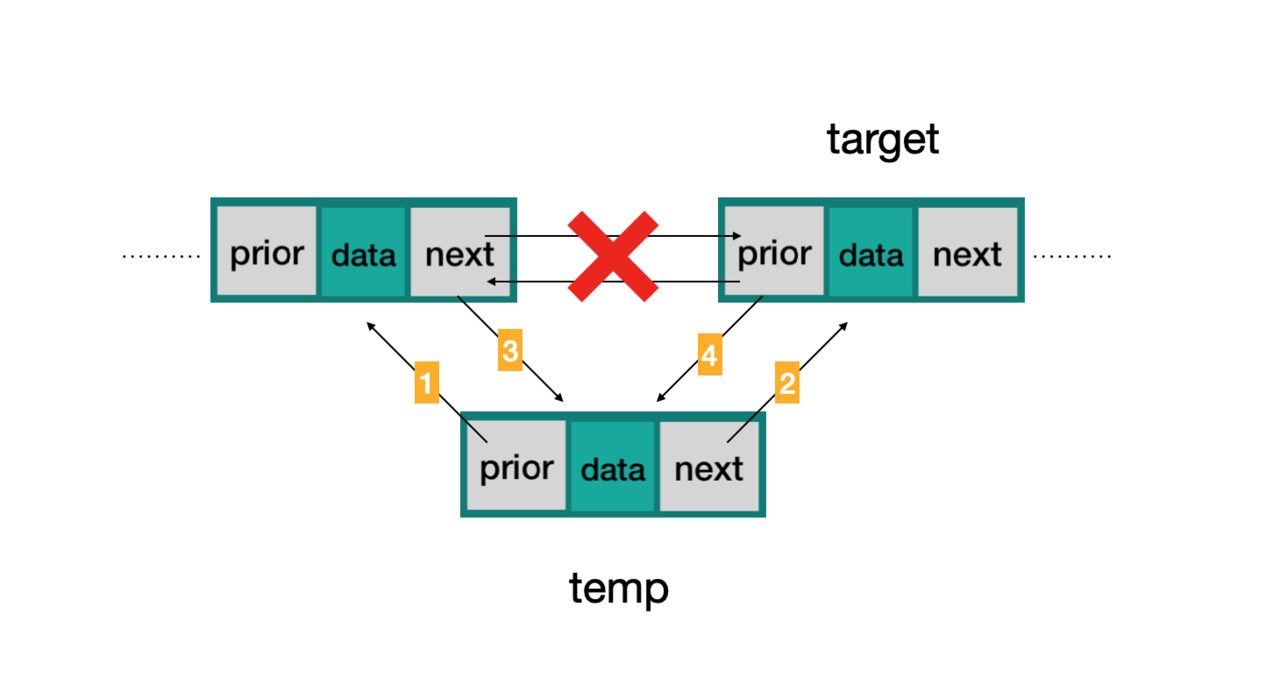
- 插入
1、 找到要插入位置的结点
2、 新建一个结点
3、 新结点的prior指向插入位置结点的前一个结点
4、 新结点的next指向要插入位置的结点
5、 前一个结点的next指向新结点
6、 插入位置的结点的prior指向新结点
Status insertLinkList(LinkList *L,int index,ElemType e){
if (*L == NULL) {
return ERROR;
}
LinkList target = (*L)->next;
int i = 1;
// 这里要查找到要插入位置的节点
while (i<index && target != (*L)) {
target = target->next;
i++;
}
if (i<index) { // 当上边的while循环结束的时候,满足结束的条件可能是因为target == (*L)
return ERROR; // 而退出循环,这时候其实i的值就是整个链表的长度,如果此时i依旧 // 小于index的话,那么插入的位置,是大于整个列表的长度,就返回错误
}
// 新结点
LinkList temp = (LinkList)malloc(sizeof(Node)); if (temp == NULL) {
return ERROR;
}
temp->data = e; // 新结点赋传进来的值
temp->prior = target->prior;
temp->next = target;
temp->prior->next = temp;
target->prior = temp;
return OK;
}
图解:
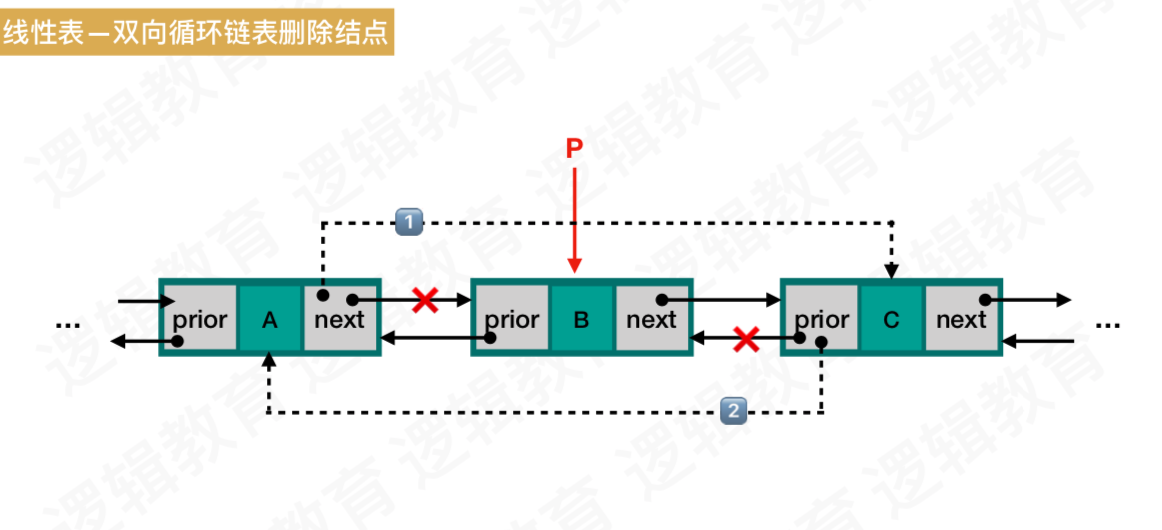
- 删除结点
1、 找到要删除的结点
2、 将前一个结点的next指向要删除结点的后一个结点
3、 将后一个结点的prior指向要删除结点的前一个结点
4、 将要删除的结点free释放空间
Status DeleteLinkList(LinkList *L,int index,ElemType *e){
if (*L == NULL) {
return ERROR;
}
LinkList deleTemp = (*L)->next;
// 判断假如链表中只剩下头结点时(可能是只有一个头结点,也可能是被删的只剩下头结点),就把链表释放掉置空,
if (deleTemp->next == *L) {
free(*L);
(*L) = NULL;
return OK;
}
int i = 1;
while (i<index && deleTemp != *L) {
deleTemp = deleTemp->next;
i++;
}
if (deleTemp == *L) { //如果index大于链表的长度,while退出的条件就是当deleTemp==*L时
printf("要删除的位置大于链表的长度\n");
return ERROR;
}
deleTemp->prior->next = deleTemp->next;
deleTemp->next->prior = deleTemp->prior;
*e = deleTemp->data; // 返回要删除的内容
free(deleTemp);
return OK;
}
图解:
- 查找
int FindLinkList(LinkList L,ElemType e){
if (L == NULL) {
return ERROR;
}
LinkList target = L->next;
int i = 1;
while (target && target != L) {
if (target->data == e) {
return i;
}
target = target->next;
i++;
}
return -1;
}
3.顺序表和链表的比较
3、1 空间性能比较
3、2 时间性能比较