算法定义:
解决特定问题求解步骤的描述,在计算机中表现为指令的有限序列,每个指令表示一个或多个操作。(简单理解:解决问题的方法)
算法特性:
1、 输入输出:至少有一个数据输入,有计算的结果输出
输入是为了确立初始条件,也可以没有
2、 有穷性:在有限的执行次数和执行时间下得到结果
3、 确定性:不同的输入要有确定的输出结果,且结果不可以有二义性
4、 可行性:每一句代码都是可执行的,在有限步骤内完成
在哪些方面去衡量?
1、 正确性
是否获得正确的结果
2、 可读性
算法阅读的难易程度
3、 健壮性
是否包含所有异常情况的处理
4、 时间效率高和储存量低
算法消耗的时间与内存空间
时间复杂度
算法的时间复杂度是一个函数,定性描述了该算法的运行时间
算法时间构成
1.算法输入的时间
2.编译可执行代码
3.执行指令
4.执行重复的指令
大O表示法计算时间复杂度
1、 用常数1取代运行时间中所有的常数 10 ->O(1)
2、 在修改运行次数函数中,只保留最高阶项 n^3+2n^2 -> O(n^3)
3、 如果最高阶存在且不等于1,则去除相乘的常数 2n^3 -> O(n^3)
常数阶
/* 1. 常数阶时间复杂度计算 O(1) *///1+1+1 = 3
大O规则第一条:常数1取代运行时间中的所有常数,即O(1) */
//1+1+1 = 3 O(1)
void testSum1(int n){
int sum = 0; //执行1次
sum = (1+n)*n/2; //执行1次
printf("testSum1:%d\n",sum);//执行1次
}
线性阶
//1+(n+1)+n+1 = 3+2n -> O(n)
void testSum3(int n){
int i,sum = 0; //执行1次
for (i = 1; i <= n; i++) { //执行n+1次
sum += i; //执行n次
}
printf("testSum3:%d\n",sum); //执行1次
}
对数阶
/*2的x次方等于n x = log2n ->O(logn)*/
void testA(int n){
int count = 1; //执行1次
//n = 10
while (count < n) {
count = count * 2;
}
}
平方阶
//1+(n+1)+n(n+1)+n^2+n^2 = 2+3n^2+2n -> O(n^2)void testSum5(int n){
int i,j,x=0,sum = 0; //执行1次
for (i = 1; i <= n; i++) { //执行n+1次
for (j = 1; j <= n; j++) { //执行n(n+1)
x++; //执行n*n次
sum = sum + x; //执行n*n次
}
} printf("testSum5:%d\n",sum);
}
立方阶
/*5.立方阶*/ O(n^3)
void testB(int n){
int sum = 1; //执行1次
for (int i = 0; i < n; i++) { //执行n次
for (int j = 0 ; j < n; j++) { //执行n*n次
for (int k = 0; k < n; k++) {//执行n*n*n次
sum = sum * 2; //执行n*n*n次
}
}
}
}
指数阶 (不做事例)
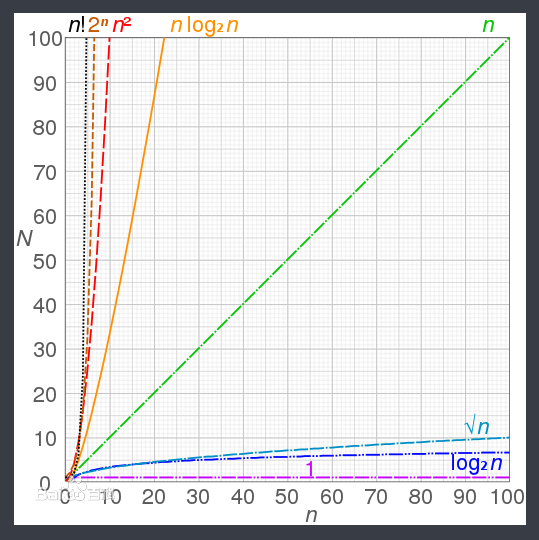
各时间复杂度的比较
空间复杂度
空间复杂度通过计算算法所需的存储空间实现,空间计算因素有
1、 寄存本身的指令
2、 常数
3、 变量
4、 输入
5、 对数据操作的辅助空间
在考量算法的空间复杂度,主要考虑算法执行时所需要的辅助空间
计算公式:S(n) = n(f(n)) // n为问题的规模 f(n)为语句关于n所占存储空间的函数
int temp; //temp为辅助空间且为常数1 则空间复杂度为O(1)
for(int i = 0; i < n/2 ; i++){
temp = a[i];
a[i] = a[n-i-1];
a[n-i-1] = temp;
}
算法衡量
1、 最优时间复杂度:完成工作最少花费时间,反映出最理想状态下结果,一般不以它参考
2、 最差时间复杂度:完成工作最多花费时间,即最糟糕的情况下算法得出结果,但是它表明算法在此种情况下一定能完成,最有参考价值
3、 平均时间复杂度:完成工作平均花费时间,也称加权平均时间复杂度或者期望时间复杂度,当最差时间复杂度相同时,可以用平均时间复杂度对比两个方法
呼应主题,测评算法是否好坏?
1.算法结果的正确性
2.算法的可阅读性,添加必要的注解,方法名等
3.算法的健壮性,对算法的输入进行容错判断,对边界值小心处理以免越界
4.时间复杂度空间复杂度的计算对比