我们知道数据结构根据数据的存储方式分为线性结构和非线性结构,而树就属于非线性结构。
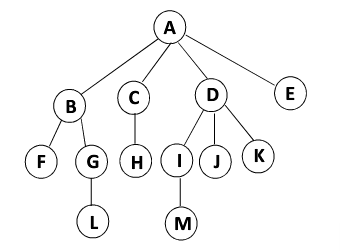
树是由n(n>0)个有限结点组成的具有层次结构的集合。 当n=0时,叫做空树。
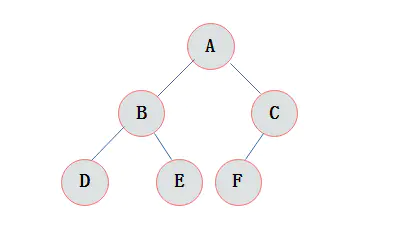
把这种数据结构叫做树是因为它看起来像一棵“倒挂的树”,即根朝上,叶朝下的树。
它具有以下特征:
- 没有父结点的树叫做根结点
- 每个结点可以有一个或多个子结点
- 每个非根结点只有一个父结点
树的基本术语
- 结点的度:结点的子树个数
- 树的度:树中所有结点的度的最大值
- 路径和路径长度:从结点n1到nk的路径是一个结点序列n1、n2、… 、nk
其中ni是ni+1的父结点。路径所包含的边的个数叫做路径的长度
- 结点的层次:规定根结点的层次为1层,其他任一结点的层次为其父结点的层次加一
- 树的深度:树中所有结点的层次最大值是这棵树的深度
二叉树
二叉树其实就是树的一种特殊情况。区别在于:
- 二叉树的每个结点最多只能有两个结点
- 二叉树中的结点是区分左右的。顺序不能颠倒
二叉树拥有如下性质:
- 在二叉树的第i层最多有2i-1个结点
- 深度为k的二叉树,最多有2k - 1 个结点 (k>=1)
- n0 = n2 + 1,n0为度数为0的结点数,n2 度数为2的结点数
斜树
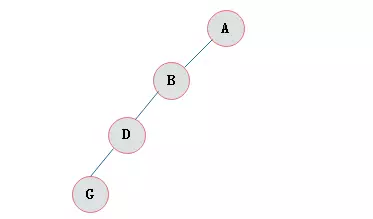
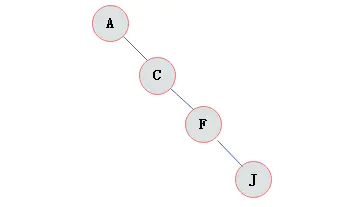
所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。
左斜树
右斜树
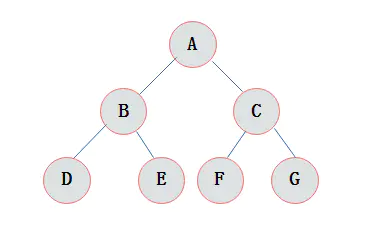
满二叉树
在一棵二叉树中。如果所有结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。
完全二叉树
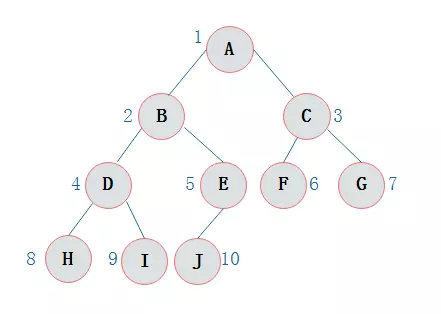
对一颗具有n个结点的二叉树按层编号,如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树。
完全二叉树的性质:
- 具有n个结点的完全二叉树的深度[log2n] + 1,其中[log2n]是向下取整。
二叉树的存储结构
二叉树的结点可以使用一维数组进行存储,或者是链表进行存储。
顺序存储
二叉树的顺序存储就是利用一维数组存储二叉树的结点,结点的存储位置就是数组的下标索引。
由此,我们知道二叉树的顺序存储结构的优点是查找效率高,而且增加和删除结点的效率高。
缺点就是当二叉树结构不是完全二叉树时,容易出现空间浪费的问题。
例如:当出现斜树的情况时,那么数组中大部分的位置都是没有存储结点的,大大浪费了空间。
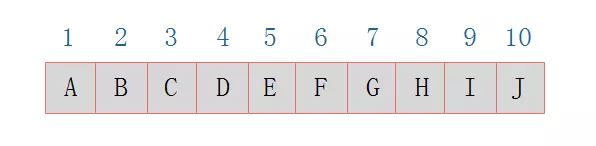
对应一维数组的存储如下:
链式存储
二叉树的链式存储就是使用链表进行结点的存储。
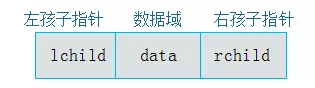
结点的结构存在一个数据域,两个指针域。
二叉树的遍历
二叉树的遍历是指从二叉树的根结点出发,按照某种次序依次访问二叉树中的所有结点,使得每个结点被访问一次,且仅被访问一次。
二叉树的访问次序可以分为四种:
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历
前序遍历
前序遍历首先访问根结点然后遍历左子树,最后遍历右子树。在遍历左、右子树时,仍然先访问根结点,然后遍历左子树,最后遍历右子树。
中序遍历
中序遍历首先遍历左子树,然后访问根结点,最后遍历右子树。在遍历左、右子树时,仍然先遍历左子树,然后访问根结点,最后遍历右子树。
后序遍历
后序遍历首先遍历左子树,然后遍历右子树,最后访问根结点,在遍历左、右子树时,仍然先遍历左子树,然后遍历右子树,最后遍历根结点。
层次遍历
层次遍历就是按照树的层次自上而下的遍历二叉树。
二叉树的代码实现
顺序存储
package com.xgc.tree.binarytree.sequentialstoreage;
public class BinaryTree {
Object[] arr;
public void buildTree(Object[] arr) {
this.arr = arr;
}
/**
* 先序遍历
* @param root 树的根结点
*/
public void preOrderTree() {
preOrderTree(0);
}
private void preOrderTree(int index) {
if (arr==null || arr.length == 0) return;
System.out.print(arr[index] + " ");
if((index*2+1)<arr.length){
preOrderTree(index*2+1);
}
if((index*2+2)<arr.length){
preOrderTree(index*2+2);
}
}
//中序和后序遍历 与 先序遍历类似,这里就不写了
//层次遍历就更简单了,遍历数组就可以了
}
链式存储
package com.xgc.tree.binarytree.linkedstoreage;
/**
* 二叉树的结点
* @author xgc
*
*/
public class TreeNode {
Object data;
//左节点
TreeNode left;
//右节点
TreeNode right;
public TreeNode(Object data) {
this.data = data;
}
public TreeNode(TreeNode left , Object data, TreeNode right) {
this.left = left;
this.data = data;
this.right = right;
}
}
package com.xgc.tree.binarytree.linkedstoreage;
/**
* 二叉树的结点
* @author xgc
*
*/
public class TreeNode {
Object data;
//左节点
TreeNode left;
//右节点
TreeNode right;
public TreeNode(Object data) {
this.data = data;
}
public TreeNode(TreeNode left , Object data, TreeNode right) {
this.left = left;
this.data = data;
this.right = right;
}
}
测试:
package com.xgc.tree.binarytree.linkedstoreage;
public class BinaryTreeTest {
public static void main(String[] args) {
Object[] arr = {1,2,3,4,5,6,7,8,9};
BinaryTree tree = new BinaryTree();
TreeNode root = tree.buildTree(arr);
System.out.print("先序遍历 ");
tree.preOrderTree(root);
System.out.println();
System.out.print("中序遍历 ");
tree.inOrderTree(root);
System.out.println();
System.out.print("后序遍历 ");
tree.postOrderTree(root);
System.out.println();
System.out.print("层次遍历 ");
tree.levelOrderTree(root);
System.out.println();
}
}
执行结果如下:
先序遍历 1 2 4 8 9 5 3 6 7
中序遍历 2 4 8 9 5 1 3 6 7
后序遍历 2 4 8 9 5 3 6 7 1
层次遍历 1 2 3 4 5 6 7 8 9
二叉搜索树
二叉搜索树:一颗二叉树,可以为空。如果不为空,满足如下性质:
- 非空左子树所有结点的值都小于根结点的值
- 非空右子树所有结点的值都大于根结点的值
- 左子树和右子树都是二叉搜索树
二叉搜索树不会出现重复元素,所以遇到重复元素的时候就不插入。
二叉搜索树操作的函数有:
- 插入新结点
- 删除结点
- 查找最大值和最小值
- 查找指定值的结点
在上面的操作中,删除结点的操作比较复杂,所以介绍删除结点操作的实现思路,其他的就不介绍了,看代码实现就可以了。
二叉搜索树的删除操作分类讨论:
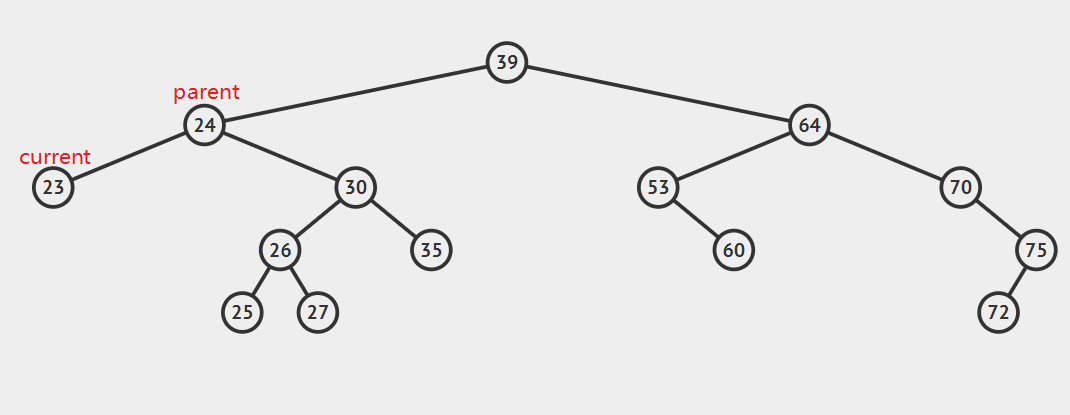
1、 要删除的结点没有子结点,即是叶节点。
这里我们将要删除结点的父结点的left或right设为NULL就可以了
这里的left、right取决于要删除的结点是父结点的左结点或右结点
像上图current是当前要删除的结点,我们只要把parent.left设为null即可
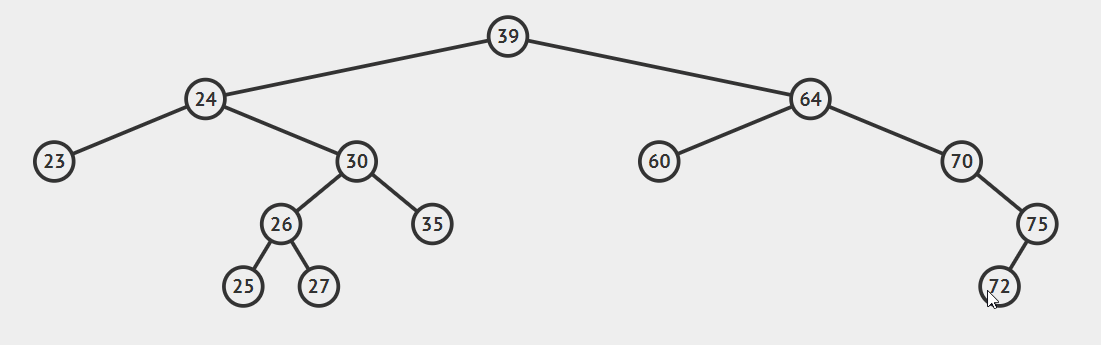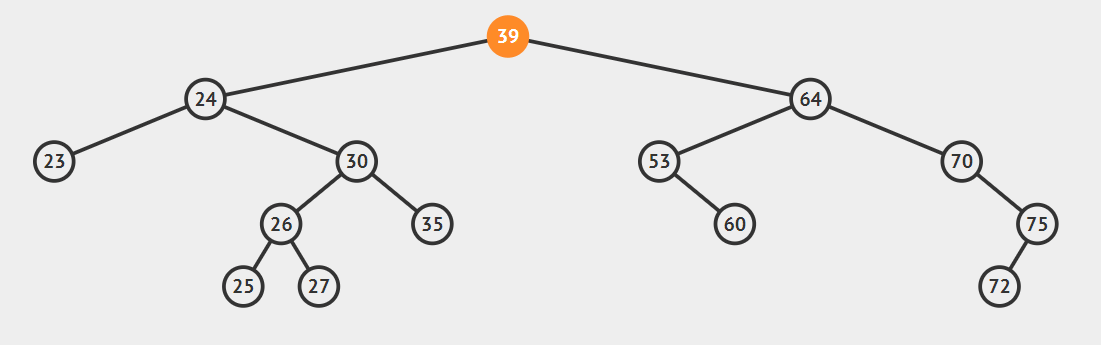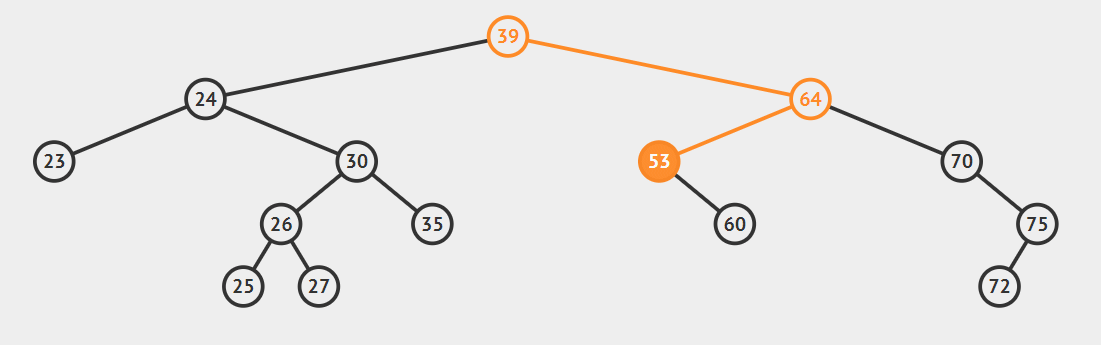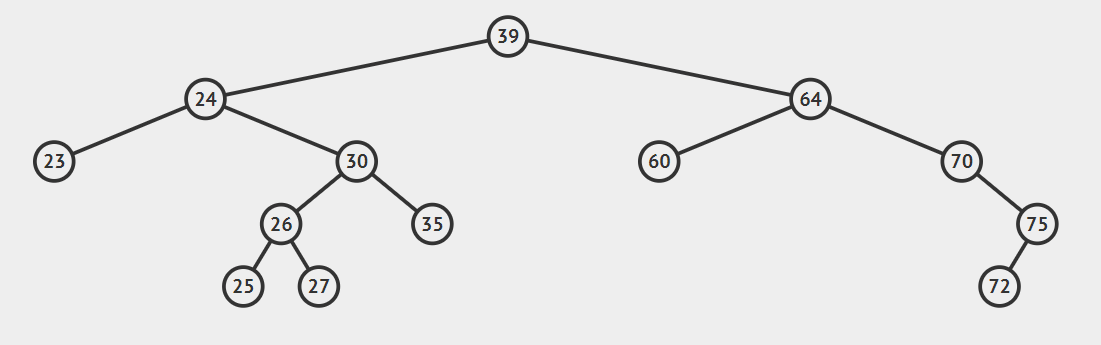
1、 删除的结点有一个孩子结点
将这个孩子结点赋值给要删除结点的父结点的left或right
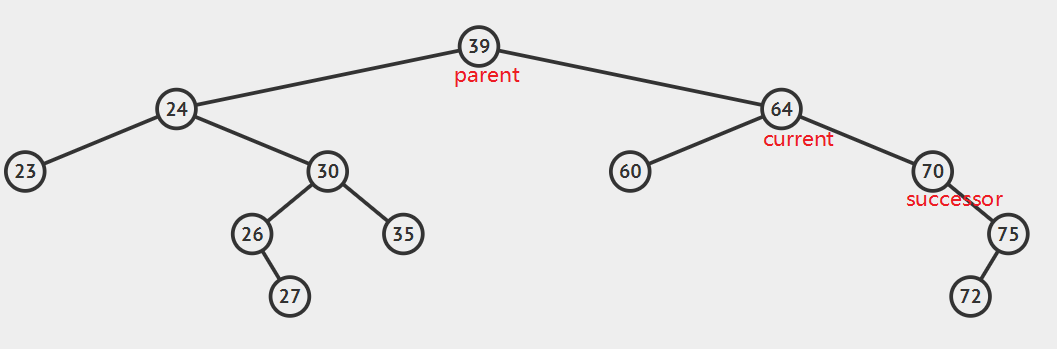
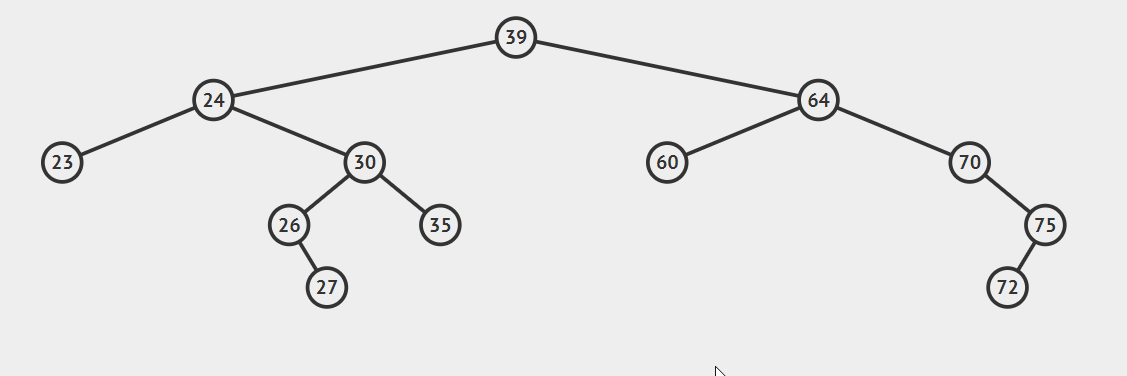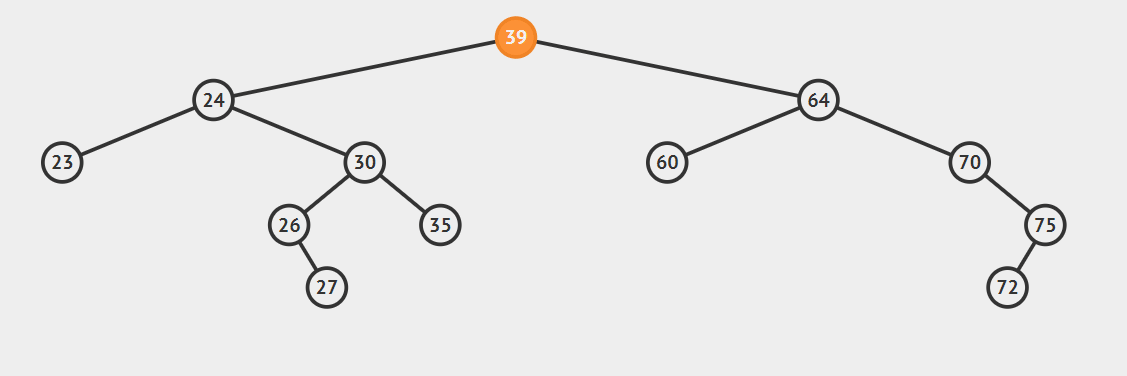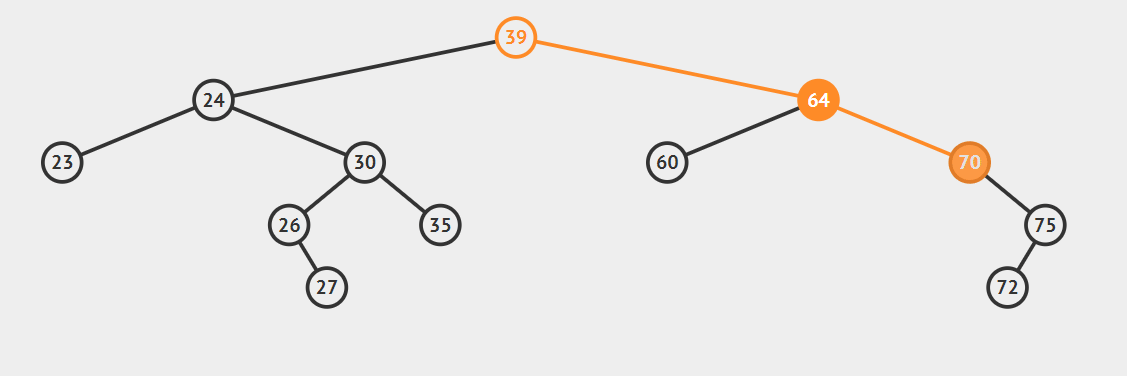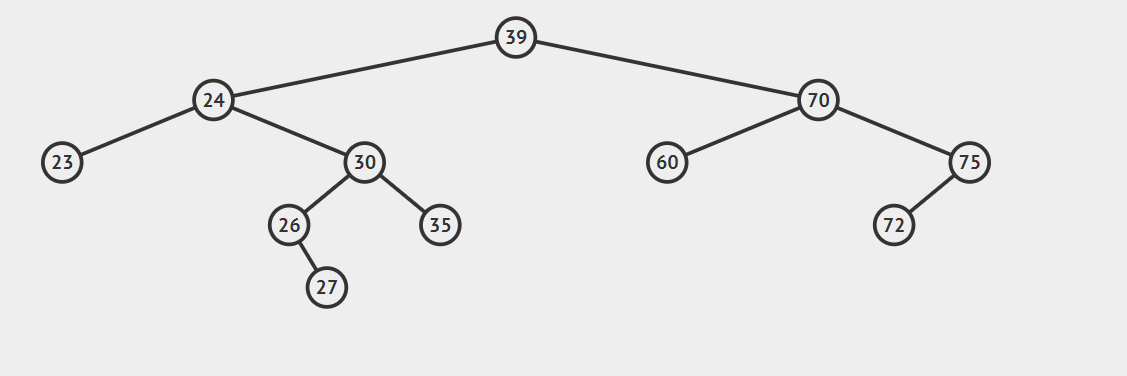
1、 要删除的结点有两个孩子结点
这种情况比较复杂,我们引入**后继结点**的概念。
后继结点:如果将一棵二叉树按照中序遍历的方式输出,则任一结点的下一个结点就是该结点的后继结点。
* **后继节点为要删除结点的右结点**
将要删除的结点用后继结点替换即可,注意处理好删除结点的left和后继结点的right
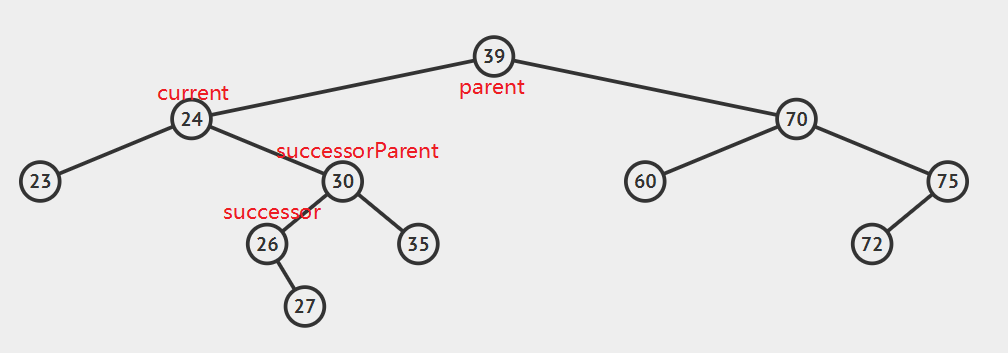
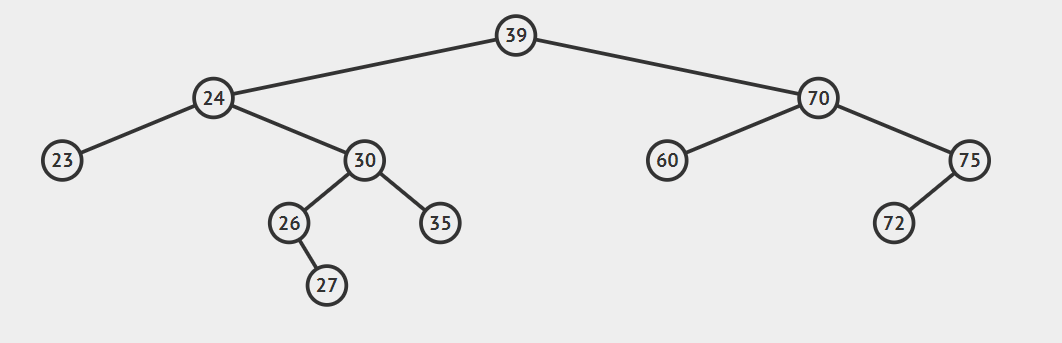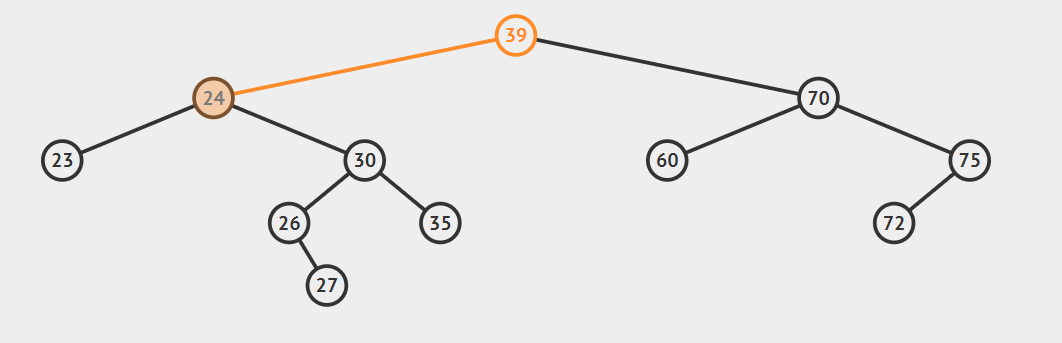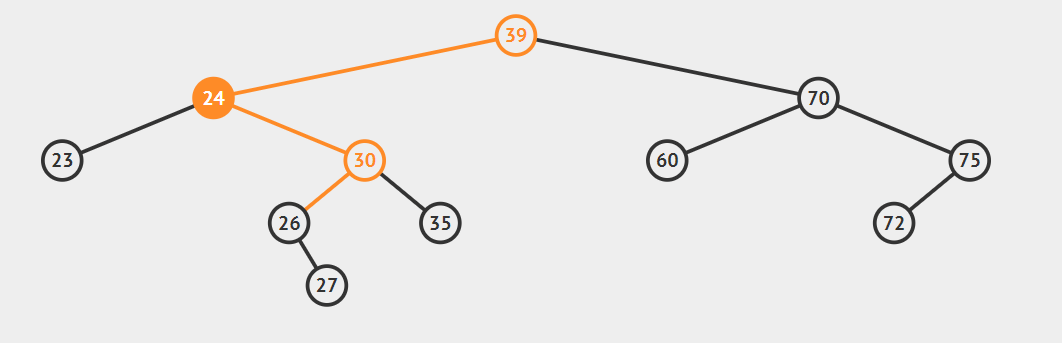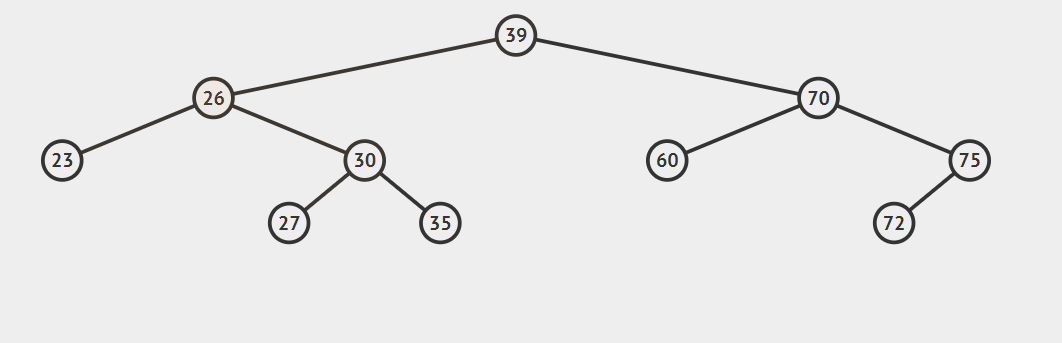
- 后继节点为要删除结点的右孩子的左子
这种情况比较复杂,看动图就明白了
二叉搜索树的代码实现
package com.xgc.tree.binarysearchtree;
import java.util.LinkedList;
import java.util.Queue;
/**
* 二叉搜索树
* @author xgc
*
*/
public class BinarySearchTree {
/**
* 二叉搜索树的结点
* @author xgc
*
*/
private class Node {
int data; // 数据域
Node right; // 右子树
Node left; // 左子树
public Node(int data) {
this.data = data;
}
public Node() {
}
}
//树的根节点
private Node root;
/**
* 根据指定的值找出二叉搜索树中对应的结点
* @param data
* @return
*/
public Node find(int data) {
Node current = root;
while(current.data != data) {
if (data > current.data) {
current = current.right;
}
if (data < current.data) {
current = current.left;
}
if (current == null) {
return null;
}
}
return current;
}
/**
* 二叉搜索树的插入
* @param data
*/
public void insert(int data) {
//要插入的结点
Node p = new Node(data);
if (root == null) {
root = p;
} else {
Node parent = new Node();
Node current = root;
while(true) {
parent = current;
if (data>current.data) {
current = current.right;
if (current==null) {
parent.right = p;
return;
}
} else if(data == current.data) {
return;
} else {
current = current.left;
if (current==null) {
parent.left = p;
return;
}
}
}
}
}
/**
* 删除指定的数据
* @param data
* @return 删除操作是否成功
*/
public boolean delete(int data) {
Node current = root;
Node parent = new Node();
boolean isRightChild = true;
//查找要删除的结点
while(current.data != data) {
parent = current;
if (data > current.data) {
current = current.right;
isRightChild = true;
} else {
current = current.left;
isRightChild = false;
}
}
//要删除的结点为叶结点
if (current.right == null && current.left == null) {
if (current == root) {
root = null;
} else {
if (isRightChild) {
parent.right = null;
} else {
parent.left = null;
}
}
return true;
}
//要删除的结点只有一个子结点
else if(current.left == null) {
if (current == root) {
root = current.right;
}else if(isRightChild) {
parent.right = current.right;
}else {
parent.left = current.right;
}
return true;
}
else if(current.right == null) {
if (current == root) {
root = current.left;
}else if(isRightChild) {
parent.right = current.left;
}else {
parent.left = current.left;
}
return true;
}
//要删除的结点有两个子结点
else {
Node successor = getSuccessor(current);
if (current == root) {
root = successor;
} else if (isRightChild) {
parent.right = successor;
} else {
parent.left =successor;
}
successor.left = current.left;
return true;
}
}
/**
* 获取给定结点的后继结点
* 不仅获取后继结点,还对删除结点的右子树结构进行了调整
* @param current
* @return 后继结点
*/
private Node getSuccessor(Node node) {
Node successorParent = node;
Node successor = node;
Node current = node.right;
while(current!=null) {
successorParent = successor;
successor = current;
current = current.left;
}
//到这里后继结点已经找好了
//如果后继结点为要删除结点的右结点的左子,调整一下要删除结点的右子树
if (successor != node.right) {
successorParent.left = successor.right;
successor.right = node.right;
}
return successor;
}
public void levelOrderTree() {
if (root == null) return;
Queue<Node> nodes = new LinkedList<>();
nodes.add(root);
while (!nodes.isEmpty()) {
Node node = nodes.poll();
System.out.print(node.data + " ");
if (node.left != null) {
nodes.add(node.left);
}
if (node.right != null) {
nodes.add(node.right);
}
}
}
public void show(Node node) {
System.out.println(node.data);
}
}
测试
package com.xgc.tree.binarysearchtree;
public class BinarySearchTreeTest {
public static void main(String[] args) {
BinarySearchTree tree = new BinarySearchTree();
tree.insert(5);
tree.insert(6);
tree.insert(7);
tree.insert(3);
tree.insert(4);
tree.insert(7);
tree.levelOrderTree();
tree.delete(3);
System.out.println();
tree.levelOrderTree();
System.out.println();
tree.show(tree.find(7));
}
}
执行结果为:
5 3 6 4 7
5 4 6 7
7