排序算法稳定性:
- 当碰到两个相同的值不进行交换,那么就说这个算法是稳定的。
- 反之,这个算法就不稳定。
简单排序
冒泡排序
冒泡排序算法是稳定的排序算法。
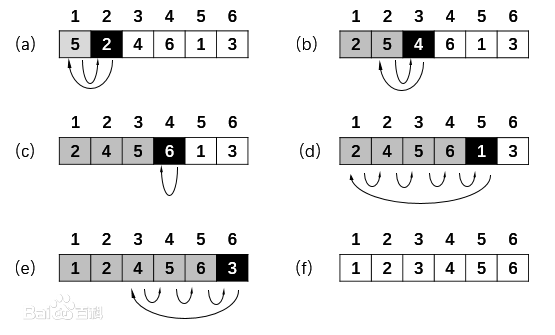
冒泡排序思路
基本思路:冒泡排序,类似于水中冒泡,较大的数沉下去,较小的数慢慢冒起来,假设从小到大,即为较大的数慢慢往后排,较小的数慢慢往前排
直观表达:每一趟遍历,将一个最大的数移到序列末尾。
算法描述
1、 第一趟排序:第1个和第2个元素比较,如果前一个比后一个大,就交换。接着第2个和第3个比较。直到倒数第2个和最后1个比较。此时,第一趟完成后,最大的元素就在序列的最后。
2、 第二趟排序:第1个和第2个元素比较,直到倒数第三和倒数第二个。
3、 不断重复,直到n-1趟。
下面为动图表示:
代码实现
package com.xgc.sort.simplesort.bubblesort;
/**
* 冒泡排序
* @author xgc
*
*/
public class BubbleSort {
public static void sort(int[] arr) {
if (arr==null || arr.length<2) {
return;
}
for(int i=0; i<arr.length-1; i++) {
for(int j=0; j<arr.length-1-i; j++) {
if (arr[j] > arr[j+1]) {
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
}
测试
package com.xgc.sort.simplesort.bubblesort;
public class BubbleSortTest {
public static void main(String[] args) {
int[] arr = {4,-1,5,9,16,10,7,4,-3};
BubbleSort.sort(arr);
for (int i : arr) {
System.out.print(i+",");
}
}
}
执行结果:
-3,-1,4,4,5,7,9,10,16,
复杂度
时间复杂度:O(n2)
空间复杂度: O(1)
稳定性:稳定
插入排序
插入排序思想
基本思想是将一个记录插入到已经排好序的有序表中,从而形成一个新的,元素个数+1的有序表。
下图为插入排序算法的排序过程表示:
代码实现
package com.xgc.sort.simplesort.insertionsort;
/**
* 插入排序
* @author 21952
*
*/
public class InsertionSort {
public static void sort(int[] arr) {
for(int i=1; i<arr.length; i++) {
//获取当前指向的元素
int temp = arr[i];
//记录在内层循环中当前指向的下标
int j;
//判断当前元素是否小于前一个元素,小于的话就开始比较并插入当前元素
//从后往前比较
for(j=i; j>0 && arr[j-1]>temp; j--) {
//将元素往后移动
arr[j] = arr[j-1];
}
//在内层循环结束之后,j指向的是temp元素要插入的位置
arr[j] = temp;
}
}
}
测试
package com.xgc.sort.simplesort.insertionsort;
public class InsertionSortTest {
public static void main(String[] args) {
int[] arr = {4,-1,5,9,16,10,7,4,-3};
InsertionSort.sort(arr);
for (int i : arr) {
System.out.print(i+",");
}
}
}
执行结果:
-3,-1,4,4,5,7,9,10,16,
复杂度
时间复杂度:O(n2)
空间复杂度: O(1)
稳定性:稳定
选择排序
选择排序思想
首先在未排序的序列中找到最小(大)元素,存放到排序序列的起始位置。然后在从剩余的未排序序列中找到最小(大)元素,放到排序序列的末尾。重复操作,直到未排序的元素为零。
代码实现
package com.xgc.sort.simplesort.selectionsort;
/**
* 选择排序
* @author xgc
*
*/
public class SelectionSort {
public static void sort(int[] arr) {
for(int i=0; i<arr.length; i++) {
//记录最小值的下标
int min=i;
for(int j=i+1; j<arr.length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
int temp = arr[i];
arr[i] = arr[min];
arr[min] = temp;
}
}
}
测试
package com.xgc.sort.simplesort.selectionsort;
public class SelectionSortTest {
public static void main(String[] args) {
int[] arr = {4,-1,5,9,16,10,7,4,-3};
SelectionSort.sort(arr);
for (int i : arr) {
System.out.print(i+",");
}
}
}
执行结果:
-3,-1,4,4,5,7,9,10,16,
复杂度
时间复杂度:O(n2)
空间复杂度: O(1)
稳定性:不稳定
希尔排序(Shell’s Sort)
希尔排序是插入排序的一种,又叫缩小增量排序,是插入排序算法的一种更高效的改进版本。
希尔排序是非稳定算法。
希尔排序基于直接插入排序的以下两个特质而提出改进方法:
1、 插入排序在几乎已经排好序的数据操作中,效率高,可以达到线性排序的效率。
2、 插入排序一般是低效的,因为插入排序每次只能将数据移动一位。
希尔排序算法思想
先取一个小于n的整数d1作为第一个增量,把所有数据进行分组,所有距离为d1的数据放在同一个组中。先在组内进行直接插入排序。然后取第二个增量d2<d1,重复上面的分组和排序,直到所取的增量dt=1,即所有数据放在同一组进行插入排序为止。
该算法之所以能够提高效率的原因是:
相隔比较远的元素的一次交换能够跨过多个元素,即进行一次交换就可能消除多个逆序对。
代码实现
package com.xgc.sort.advancedsorting.shellsort;
/**
* 希尔排序
* @author xgc
*
*/
public class ShellSort {
public static void sort(int[] arr) {
//计算增量step,这里我们也叫步长
//增量初始为长度的一半,此外不断除2,直到step==1
for(int step= arr.length/2; step>0; step/=2) {
for(int i = step; i<arr.length; i++) {
//记录要比较的数值
int temp = arr[i];
//记录内层循环当前指向的下标
int j;
for(j=i-step; j>=0 && arr[j]>temp; j-=step) {
arr[j+step] = arr[j];
}
arr[j+step] = temp;
}
}
}
}
测试
package com.xgc.sort.advancedsorting.shellsort;
public class ShellSortTest {
public static void main(String[] args) {
int[] arr = {4,-1,5,9,16,10,7,4,-3};
ShellSort.sort(arr);
for (int i : arr) {
System.out.print(i+",");
}
}
}
执行结果
-3,-1,4,4,5,7,9,10,16,
复杂度
时间复杂度:这个没有确定,根据增量序列的选择不同会有不同的时间复杂度。在上面的代码实现使用的是希尔增量序列。
空间复杂度: O(1)
稳定性:不稳定
堆排序(Heap Sort)
堆排序是指利用堆这种数据结构所设计的一种排序算法。
堆是一个近似完全二叉树的结构。
- 最大堆:每个结点的值大于或等于其子结点的值,在堆排序算法中用于升序排序
- 最小堆:每个结点的值小于或等于其子结点的值,在堆排序算法中用于降序排序
堆排序思想
1、 将给定的无序序列构造成最大堆,此时最大的元素在堆首。
2、 将堆首和堆尾交换,即将最大的元素沉到数组的末端
3、 将堆的大小减1,再调整成最大堆。
4、 不断重复至堆的大小为1
网上看堆排序,发现有篇文章的图解助于理解堆排序的过程,结合代码看,如下:
代码实现
package com.xgc.sort.advancedsorting.heapsort;
/**
* 堆排序(最大堆,升序排序)
* @author xgc
*
*/
public class HeapSort {
public static void sort(int[] arr) {
//用于记录堆长度
int len = arr.length;
//构建最大堆
//从最后一个非叶结点开始从右往左,从下往上开始调整
for(int i=arr.length/2-1; i>=0; i--) {
heapify(arr, i, len);
}
//将堆首和堆尾交换,并将堆长度减一,调整剩下堆为最大堆
for(int i = arr.length-1; i>0; i--) {
swap(arr, 0, i);
heapify(arr, 0, i);
}
}
/**
* 调整成最大堆(仅在最大堆已建立的基础上)
* @param arr 要调整的数组
* @param i 保证i结点所在的树为最大堆
* @param len 要调整的堆的长度
*/
private static void heapify(int[] arr, int i, int len) {
//最大值的下标
int largest = i;
//i节点的左子结点的下标
int left = 2*i+1;
//i节点的右子结点的下标
int right = 2*i+2;
if (left<len && arr[left]>arr[largest]) {
largest = left;
}
if (right<len && arr[right]>arr[largest]) {
largest = right;
}
if (largest != i) {
swap(arr, i, largest);
heapify(arr, largest, len);
}
}
/**
* 将i结点和最大值的结点交换
* @param arr
* @param i
* @param largest
*/
private static void swap(int[] arr, int i, int largest) {
int temp = arr[i];
arr[i] = arr[largest];
arr[largest] = temp;
}
}
测试
package com.xgc.sort.advancedsorting.heapsort;
public class HeapSortTest {
public static void main(String[] args) {
int[] arr = {4,-1,5,9,16,10,7,4,-3};
HeapSort.sort(arr);
for (int i : arr) {
System.out.print(i+",");
}
}
}
执行结果如下:
-3,-1,4,4,5,7,9,10,16,
复杂度
时间复杂度:O(nlogn)
空间复杂度: O(1)
稳定性:不稳定
归并排序(Merge Sort)
归并排序是建立在归并操作上的一种有效的排序算法。
该算法是分治法(Divide and Conquer)的一个典型的应用。
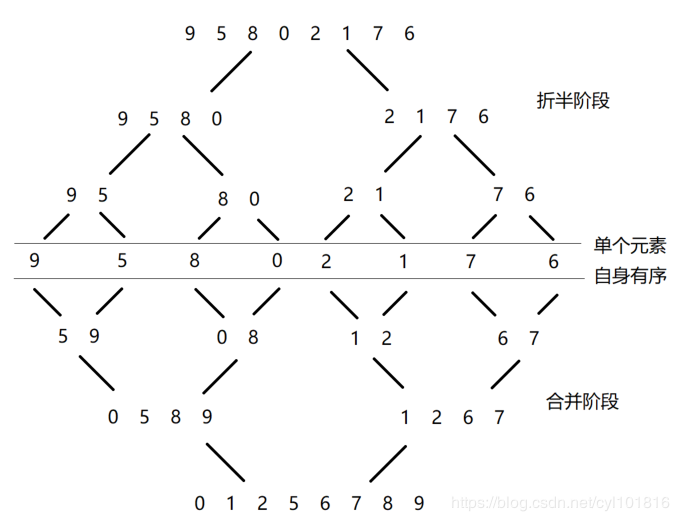
归并排序思想
1、 申请空间,使其大小为两个已排序序列之和,该空间用来存放合并后的序列
2、 设定两个指针,分别指向两个已排序序列的起始位置
3、 比较两个指针指向的元素,选择小的元素放在合并空间,并移动指针到下一位置
4、 重复步骤3,直到某一个指针超出序列尾,将另外一个序列的所有剩余元素直接赋值到合并序列尾
图解如下:图源)
代码实现
package com.xgc.sort.advancedsorting.mergesort;
public class MergeSort {
public static void sort(int[] arr) {
if (arr.length<2) {
return;
}
//合并序列的存储空间
int[] tmp = new int[arr.length];
merge(arr, 0, arr.length-1, tmp);
}
/**
* 采用分治法来实现数组的排序
* @param arr 要排序的数组
* @param start 数组的起始下标
* @param end 数据的终点下标
*/
private static void merge(int[] arr, int start, int end, int[] tmp) {
//判断传进来的start和end之间包含的元素个数是否为1
//不是的话,继续分
if (end - start > 0) {
int middle = (start+end)/2;
//对左半部分进行排序
merge(arr, start, middle, tmp);
//对右半部分进行排序
merge(arr, middle+1, end, tmp);
//左右部分排序完成后开始排序
//记录左半部分的指针
int left = start;
//记录右半部分的指针
int right = middle+1;
//记录有序序列的下标
int index = start;
//将数组排序后两部分赋值到tmp数组对应的位置
for(int i=start; i<=middle; i++) {
tmp[i] = arr[i];
}
for(int i=middle+1; i<=end; i++) {
tmp[i] = arr[i];
}
//开始比较
while(left<=middle && right<=end) {
if (tmp[left]<tmp[right]) {
arr[index++] = tmp[left++];
} else {
arr[index++] = tmp[right++];
}
}
//将剩余部分赋值
while(left<=middle) {
arr[index++] = tmp[left++];
}
while(right<=end) {
arr[index++] = tmp[right++];
}
}
}
}
测试
package com.xgc.sort.advancedsorting.mergesort;
public class MergeSortTest {
public static void main(String[] args) {
int[] arr = {4,-1,5,9,16,10,7,4,-3};
MergeSort.sort(arr);
for (int i : arr) {
System.out.print(i+",");
}
}
}
执行结果:
-3,-1,4,4,5,7,9,10,16,
复杂度
时间复杂度:O(nlogn)
空间复杂度: O(n)
稳定性:稳定
快速排序(Quick Sort)
快速排序是对冒泡排序的一种改进
快速排序思想
1、 从要排序的数据挑出一个元素,称为基准。
2、 重新排序数列,比基准小的放在基准前面,比基准大的放在基准后面。
3、 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;
代码实现
package com.xgc.sort.advancedsorting.quicksort;
public class QuickSort {
public static void sort(int[] arr) {
quicksort(arr, 0, arr.length-1);
}
/**
* 递归进行快速排序
* @param arr 要排序的数组
* @param left 要排序部分的开始下标
* @param right 要排序部分的结束下标
*/
private static void quicksort(int[] arr, int left, int right) {
if(left<right) {
int partitionIndex = partition(arr, left, right);
quicksort(arr, left, partitionIndex-1);
quicksort(arr, partitionIndex+1, right);
}
}
/**
* 将大于基准值的数放在基准值右边,将小于基准值的数放在基准值左边
* @param arr 要排序的数组
* @param left 要排序部分的开始下标
* @param right 要排序部分的结束下标
* @return 基准数的下标
*/
private static int partition(int[] arr, int left, int right) {
//记录基准值的下标
int pivot = left;
while(left<right) {
while (arr[pivot] <= arr[right] && left<right) {
right--;
}
while (arr[pivot] >= arr[left] && left<right) {
left++;
}
if (left<right) {
int tmp = arr[left];
arr[left] = arr[right];
arr[right] = tmp;
}
}
int tmp = arr[pivot];
arr[pivot] = arr[left];
arr[left] = tmp;
return left;
}
}
测试
package com.xgc.sort.advancedsorting.quicksort;
public class QuickSortTest {
public static void main(String[] args) {
int[] arr = {4,-1,5,9,16,10,7,4,-3};
QuickSort.sort(arr);
for (int i : arr) {
System.out.print(i+",");
}
}
}
执行结果:
-3,-1,4,4,5,7,9,10,16,
复杂度
时间复杂度:O(nlogn)
空间复杂度: O(1)
稳定性:不稳定
计数排序(Counting Sort)
计数排序是一种非基于比较的排序算法。它的优势在于对一定范围内的整数排序时,快于任何比较排序算法。这是一种牺牲空间换取时间的做法。
计数排序思想
对于一定范围内的整数,即在[m,n]范围整数的比较:
1、 开辟一个新数组B,该数组长度为整数n-m+1
2、 遍历数组,统计每个值为i的个数,存到数组B下标为i-m的位置
3、 反向填充数组:将数组B中的值>0的数的下标i+m,赋值到目标数组,并将对应值减一
代码实现
package com.xgc.sort.advancedsorting.countingsort;
/**
* 计数排序
* @author xgc
*
*/
public class CountingSort {
public static void sort(int[] arr) {
int[] values = getValue(arr);
int minValue = values[0];
int maxValue = values[1];
int[] newArr = new int[maxValue-minValue+1];
//遍历数组并计算同值的个数,赋值到新数组对应位置
for(int value: arr) {
newArr[value-minValue]++;
}
//反向填充目标数组
int index = 0;
for(int i=0; i<newArr.length; i++) {
while (newArr[i] > 0) {
arr[index++] = i+minValue;
newArr[i]--;
}
}
}
/**
* 获取最小值和最大值的数组
* @param arr
* @return 数组长度为2,第一个为最小值,第二个为最大值
*/
private static int[] getValue(int[] arr) {
int maxValue = arr[0];
int minValue = arr[0];
for(int value: arr) {
if (value>maxValue) {
maxValue = value;
} else if (value < minValue) {
minValue = value;
}
}
int[] value = {minValue, maxValue};
return value;
}
}
测试
package com.xgc.sort.advancedsorting.countingsort;
public class CountingSortTest {
public static void main(String[] args) {
int[] arr = {4,-1,5,9,16,10,7,4,-3};
CountingSort.sort(arr);
for (int i : arr) {
System.out.print(i+",");
}
}
}
执行结果:
-3,-1,4,4,5,7,9,10,16,
复杂度
时间复杂度:O(n + k),k为整数的范围
空间复杂度: O(n+k)
稳定性:稳定
桶排序(Bucket Sort)
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效,我们需要做到这两点:
1、 在额外空间充足的情况下,尽量增大桶的数量
2、 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中
同时,对于桶中元素的排序,选择何种比较排序算法对于性能的影响至关重要。
桶排序思想
1、 将待排序数据分到有限数量的桶子里。
2、 每个桶子再分别排序(可以使用别的排序算法或递归使用桶排序进行排序)
代码实现
这里对每个桶使用了插入排序,具体代码见上面的 简单排序->插入排序 一节
package com.xgc.sort.advancedsorting.bucketsort;
import java.util.Arrays;
import com.xgc.sort.simplesort.insertionsort.InsertionSort;
public class BucketSort {
/**
* 桶排序
* @param arr 要排序的数组
* @param bucketSize 每个桶的大小
*/
public static void sort(int[] arr, int bucketSize) {
if (arr.length==0) {
return;
}
int minValue = arr[0];
int maxValue = arr[0];
for (int value : arr) {
if (value < minValue) {
minValue = value;
} else if(value > maxValue) {
maxValue = value;
}
}
int bucketCount = (int)Math.floor((maxValue-minValue) / bucketSize) + 1;
int[][] buckets = new int[bucketCount][0];
//利用映射函数将数据分配到各个桶中
//索引为i的桶存放的数据都比索引为i+1的桶大
for (int i = 0; i < arr.length; i++) {
int index = (int)Math.floor((arr[i]-minValue) / bucketSize);
buckets[index] = arrAppend(buckets[index], arr[i]);
}
int arrIndex = 0;
for(int[] bucket: buckets) {
if (bucket.length<=0) {
continue;
}
//对每个桶进行排序,这里使用插入排序
InsertionSort.sort(bucket);
for (int value : bucket) {
arr[arrIndex++] = value;
}
}
}
/**
* 对桶自动扩容,并且保存数据
* @param arr 桶
* @param value 要保存的数组
* @return 扩容并保存了数据的桶
*/
private static int[] arrAppend(int[] arr, int value) {
arr = Arrays.copyOf(arr, arr.length+1);
arr[arr.length-1] = value;
return arr;
}
}
测试
package com.xgc.sort.advancedsorting.bucketsort;
public class BucketSortTest {
public static void main(String[] args) {
int[] arr = {4,-1,5,9,16,10,7,4,-3};
BucketSort.sort(arr, 3);
for (int i : arr) {
System.out.print(i+",");
}
}
}
执行结果如下:
-3,-1,4,4,5,7,9,10,16,
复杂度
时间复杂度:O(n + c),c = N*(logN – logM),n为待排序数据个数,m为桶的个数
空间复杂度: O(n+m)
稳定性:稳定
基数排序(Radix Sort)
基数排序是一种非比较型整数排序算法。
基数排序思路
基数排序思路是将整数按位数切割成不同的数字,然后按每个位数分别比较
动图展示如下:
代码实现
package com.xgc.sort.advancedsorting.radixsort;
import java.util.Arrays;
/**
* 基数排序(包括负数)
* @author xgc
*
*/
public class RadixSort {
public static void sort(int[] arr) {
int maxDigit = getMaxDigit(arr);
int mod = 10;
int dev = 1;
for(int i=0; i<maxDigit; i++, mod*=10, dev*=10) {
// 考虑负数的情况,这里扩展一倍队列数,其中 [0-9]对应负数,[10-19]对应正数 (bucket + 10)
// 每一轮counter都会扩大10倍,第二轮[0,99]对应负数,[100,199]对应正数
int[][] counter = new int[mod * 2][0];
for (int j = 0; j < arr.length; j++) {
//要是不考虑整数 bucket = arr[j]/dev
//此处的计算是考虑了负数的情况
int bucket = ((arr[j] % mod) / dev) + mod;
counter[bucket] = arrayAppend(counter[bucket], arr[j]);
}
int pos = 0;
for (int[] bucket : counter) {
for (int value : bucket) {
arr[pos++] = value;
}
}
}
}
/**
* 获取数组中数据的最大位数
* @param arr
* @return 最大位数
*/
private static int getMaxDigit(int[] arr) {
int maxValue = getMaxValue(arr);
return getNumLength(maxValue);
}
/**
* 获取数组中的最大值
* @param arr
* @return 最大值
*/
private static int getMaxValue(int[] arr) {
int maxValue = arr[0];
for (int value : arr) {
if (value > maxValue) {
maxValue = value;
}
}
return maxValue;
}
/**
* 获取指定值的位数
* @param value 指定值
* @return 位数
*/
private static int getNumLength(int value) {
if (value==0) {
return 1;
}
int length = 0;
for(int temp = value; temp!=0; temp/=10) {
length++;
}
return length;
}
/**
* 扩容数组并保存数据
* @param arr 要扩容并保存数据的数组
* @param value 要保存的数据
* @return 扩容并保存数据后的数组
*/
private static int[] arrayAppend(int[] arr, int value) {
arr = Arrays.copyOf(arr, arr.length + 1);
arr[arr.length - 1] = value;
return arr;
}
}
测试
package com.xgc.sort.advancedsorting.radixsort;
public class RadixSortTest {
public static void main(String[] args) throws Exception {
int[] arr = {4,-1,5,9,16,10,7,4,-3};
RadixSort.sort(arr);
for (int i : arr) {
System.out.print(i+",");
}
}
}
执行结果:
-3,-1,4,4,5,7,9,10,16,
复杂度
时间复杂度:O(d(r+n)),序列中最大值的位数为d,数字的基数为r,序列中元素个数为n
空间复杂度: O(rd+n)
稳定性:稳定