并查集的作用
集合并、查某元素属于什么集合
并查集问题中集合存储如何实现
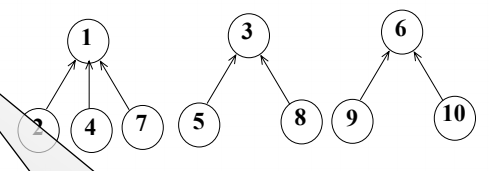
1、 可以用树结构表示集合,树的每个结点代表一个集合元素
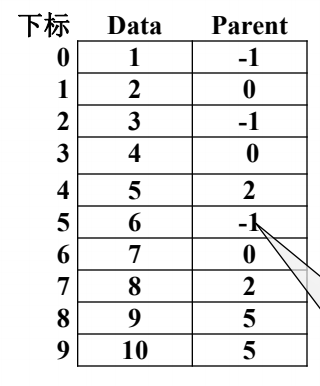
2、 采用数组存储形式
使用数组存储更加方便
数组的存储形式
对应的关系
实现思路
并操作:将一个集合的根结点指向另一个集合的根节点(一般是将小集合的根结点指向大集合的根节点,这样做查找效率更高)
查操作:查找该元素所在树的根结点
代码实现
//查找某个元素所在的集合(用根结点表示)
int Find( SetType S[ ], ElementType X ) {
/* 在数组S中查找值为X的元素所属的集合 */
/* MaxSize是全局变量,为数组S的最大长度 */
int i;
for ( i=0; i < MaxSize && S[i].Data != X; i++) ;
if( i >= MaxSize ) return -1; /* 未找到X,返回-1 */
for( ; S[i].Parent >= 0; i = S[i].Parent ) ;
return i; /* 找到X所属集合,返回树根结点在数组S中的下标 */
}
//分别找到X1和X2两个元素所在集合树的根结点
//如果它们不同根,则将其中一个根结点的父结点指针设置成另一个根结点的数组下标。
void Union( SetType S[ ], ElementType X1, ElementType X2 )
{
int Root1, Root2;
Root1 = Find(S, X1);
Root2 = Find(S, X2);
if( Root1 != Root2 )S[Root2].Parent = Root1;
}
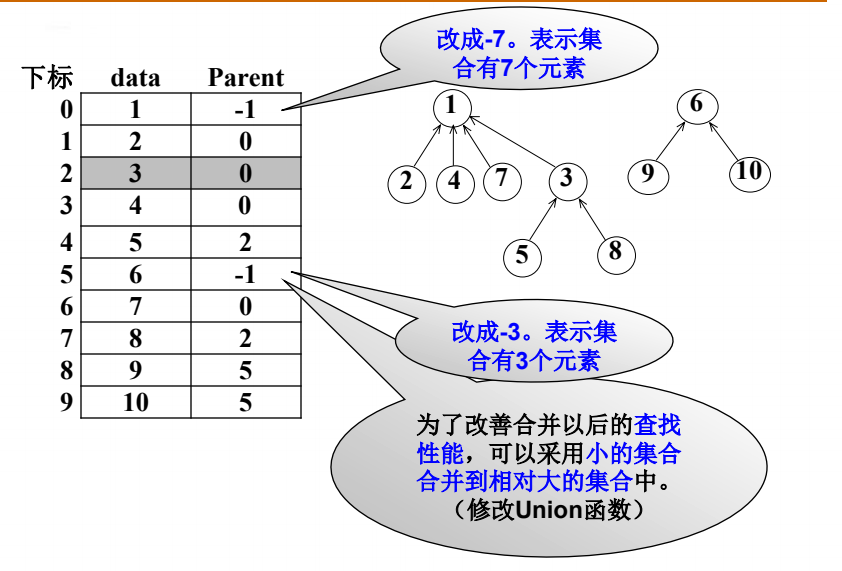
优化
为了改善合并以后的查找性能,可以采用小的集合合并到相对大的集合中。(修改Union函数)
既然要比较大小,就要记录集合的元素个数
我们可以在集合的根结点上的父元素填入集合的元素个数
如下