哈夫曼树的定义

在了解哈夫曼树的定义之前，我们先了解什么是带权路径长度

最优二叉树或哈夫曼树: WPL最小的二叉树

哈夫曼树的构造

哈夫曼树的构造方法：每次把权值最小的两颗二叉树合并

typedef struct TreeNode *HuffmanTree;
struct TreeNode{
    int Weight;
    HuffmanTree Left, Right;
}
HuffmanTree Huffman( MinHeap H ) { 
    /* 假设H->Size个权值已经存在H->Elements[]->Weight里 */
    int i; HuffmanTree T;
    BuildMinHeap(H); /*将H->Elements[]按权值调整为最小堆*/
    for (i = 1; i < H->Size; i++) { /*做H->Size-1次合并*/
        T = malloc( sizeof( struct TreeNode) ); /*建立新结点*/
        T->Left = DeleteMin(H);/*从最小堆中删除一个结点，作为新T的左子结点*/
        T->Right = DeleteMin(H);/*从最小堆中删除一个结点，作为新T的右子结点*/
        T->Weight = T->Left->Weight+T->Right->Weight;/*计算新权值*/
        Insert( H, T ); /*将新T插入最小堆*/
    }
    T = DeleteMin(H);
    return T;
}

哈夫曼树的特点

• 没有度为1的结点
• 哈夫曼树的任意非叶节点的左右子树交换后仍是哈夫曼树
• n个叶子结点的哈夫曼树共有2n-1个结点

哈夫曼编码

引例

给定一段字符串，如何对字符进行编码，可以使得该字符串的编码 存储空间最少？

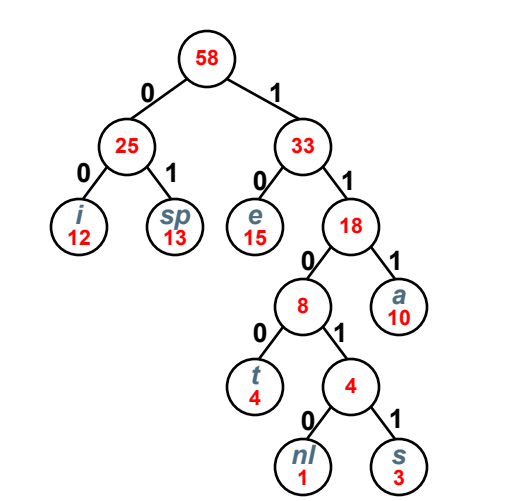
假设有一段文本，包含58个字符，并由以下7个字符构：a，e，i， s，t，空格（sp），换行（nl）；这7个字符出现的次数不同。如何对 这7个字符进行编码，使得总编码空间最少？

分析

1、 用等长ASCII编码：58 ×8 = 464位；
2、 用等长3位编码：58 ×3 = 174位；
3、 不等长编码：出现频率高的字符用的编码短些，出现频率低 的字符则可以编码长些？

显然使用不等长编码，可以使得总编码空间最少！

不等长编码的方法

我们将字符作为结点，将各字符出现的频率作为权值。很自然，我们就会想到哈夫曼树。因此，我们可以将各结点构造成哈夫曼树。

下面是不等长编码的例子：

我们可以构造成哈夫曼树

将左边设为0，右边设为1，我们可以得到下面的编码

这就是哈夫曼编码

文章永久链接：https://tech.souyunku.com/40768