Scala之：FP与OOP && 函数初级-搜云库技术团队

在Java中，函数（在一个类中声明的函数，我们更倾向于称之为方法，行为）的创建要依赖于类，抽象类，或者接口。而Scala推崇函数式编程，函数被视作“一等公民”，它可以像变量一样，即可以作为函数的参数使用，也可以将函数赋值给另一个变量。

当然，在开篇之前，与其介绍枯燥的语法，不如抽出5分钟的时间来思考这样一个问题：在OOP大行其道的今天，FP又带给我们什么呢？

其实，有关于OOP和FP的争论由来已久，笔者尚未有资历对其任何一派指点江山，因此在这里奉行中庸之道：纯粹的OOP和纯粹的FP都是极端的；而我们都知道，物极必反。还有一点，任何脱离实际开发应用的背景而对编程范式大谈特谈是没有意义的。

有关FP和OOP的总结来自于以下优质文章，知乎上的牛人还是很多的。

在开场之前：为什么要使用OOP编程

OOP，是一种设计思想，而非Java / Cpp 语言的特权。我们不如去看看OO语言之父Alan Key是怎么说的：

I thought of objects being like biological cells and/or individual computers on a network, only able to communicate with messages (so messaging came at the very beginning — it took a while to see how to do messaging in a programming language efficiently enough to be useful). … OOP to me means only messaging, local retention and protection and hiding of state-process, and extreme late-binding of all things. It can be done in Smalltalk and in LISP.

“我认为OOP应该是构造了网络结构（就像细胞构成了组织，或是电脑构成了互连网络），每个节点间通过发送消息来进行沟通。…OOP于我而言，只是每个对象保有内部隐藏的信息，但是允许通过交换信息来进行有限的沟通”。

OOP思想非常适合编写庞大且复杂的系统。一个典型的例子是Linux内核，它充分体现了多个相对独立的组件（进程调度器、内存管理器、文件系统……）之间相互协作的思想。尽管Linux内核是用C写的，但是他比很多用所谓OOP语言写的程序更加OOP。

OOP的优势一定要到了根本就不可能有一个“上帝视角”的存在纵观全局，而不得不把系统拆成很多Object时才会体现出来。就比如，公司要分很多个部门，每个部门相对的独立，有自己的章程，办事方法和规则等。各部门“隐藏内部状态”，也就是说，各个部门之间是独立的。比如你想让某部门按照章程办一件事，从来不关心“谁会做”，“他们会如何做” 这些内部细节，你需要知道只管他们会帮你办妥即可。

通过这种松散的协作关系维系的系统可以无限扩展下去，形成庞大的，复杂的系统。这就是OOP想表达的思想，仅此而已。笔者不赞同将OOP和 “继承，封装，多态”绑定在一起：如果只是为了OOP而OOP，那恐怕其冗杂的系统所带来的维护成本要更高。

题外话，Scala的设计者看来就对Java的继承机制不那么满意。比如具备继承关系的三代：祖父，父亲，儿子。父亲继承了来自祖父的属性/方法，但是儿子可能对这些特性并不怎么感兴趣。然而按照严格的继承法则，儿子却不得不收下这沉甸甸的“父爱”，将冗余而又无用的属性/方法一路继承下去。

我们在介绍Scala的特质 Trait 时会接着探讨这个问题。

FP能带给我们什么

函数式编程更加关注于数据的映射关系：我输入一个x，并希望通过f(x)变换之后，得到一个对应的结果y。并且在理想情况下：只要我输入的x不变，那我得到的y也绝对不会变（满足这种条件的称之为纯函数）。我们常常将多个函数组合起来使其变成一条封闭的，长长的流水线，比如描述这样的过程：

//无任何全局变量
//定义函数
f(白菜，土豆，胡萝卜) => (饭)
g(吃的) => if(吃的!=null) (饱了) else (饿了)
h(饥饿状态) => if(饥饿状态==饱了) (工作) else (摸鱼)
-------Main------------
h(g(f(白菜，土豆，胡萝卜)))

等等，这难道不是面向过程编程么？

函数式编程强调：隔离副作用，即不会依赖也不会改变当前函数以外的数据。所有其他的“函数式”的东西都源于此：包括纯函数，函数柯里化，高阶函数。（我们在后续的函数高级部分介绍Scala是如何使用它们的）

面向过程编程使用了外部变量来表示状态，而不是传入参数。方法通过改变外部变量影响了附近的代码，而不是通过返回值。为了搞清楚方法做了什么，读者必须仔细阅读每行。如果发现一个外部变量，必须找他它的出处，找到有哪些方法修改了它，并且要知道这样做的后果：这个变量的变化会引起哪些连锁反应。

而函数式编程中，所有的玄机都在这个函数内部。你只要知道一件事：你输入了什么，并且会因此得到什么。

(下面是笔者所理解的，面向过程的解决思路)

//全局变量dinner 和 hungry
吃的 = null;
饥饿状态 = true;
//定义函数
f(白菜，土豆，胡萝卜) => 吃的 = 晚饭;
g() => if(吃的!=null) 饥饿状态 = false;
h() => if(饥饿状态!=true) (工作) else (摸鱼);
-------Main------------
f(白菜，土豆，胡萝卜);
g();
h();

In short：函数式语言，每次一个步骤方法会产生一个状态，这个状态会直接当参数传进下一步中，而不是使用全局变量。

最后来谈谈FP适用的场景：如果是那种“第一步”、“第二步“……的程序，面向数据的程序，极致为性能做优化的程序，FP要比OOP更加适合，比如Spark的RDD（弹性分布式数据集）就将FP的思想发扬光大，以及Java 8 的Stream流处理过程。

（网图：似乎OOP世界中一切的设计模式在FP看来都是花里胡哨……HHHHH只是开个玩笑。）

在Scala中定义一个函数

我们出于学习Scala的目的，首先要迈出第一步：如何定义一个Scala函数。Scala函数可以这么定义：

//定义函数的完整写法。
def function(p: ParamType) : ReturnType = {...}

//定义函数时，允许省略返回值类型。
//这不代表不返回值，而是取决于此函数最后一个可以返回值的语句。
def function(p : ParamType) = {...}

//注意，这是空括号函数。
def function() = {...}

//注意，这是无参数函数。
def funtion = {...}

//这个函数允许有多个参数列表。（这种声明与函数柯里化相关。）
def function()()() ={...}

和 Java 那种严肃的方法声明相比，Scala的函数定义显得相当放荡且随意。（还没考虑到泛型参数，默认参数赋值，隐式参数等情况……）不过目前为止，我们先记住前两种方式就足够了。

Scala允许在定义函数的时候省去具体的返回值类型，这样，Scala就会使用类型推断来判断函数的返回值。

1、如果Scala知道此函数具备返回值，但是无法推断详细类型，则默认返回值为Any类型。
2、如果Scala认为此函数不具备返回值，则默认返回值为Unit。
3、 Scala的参数列表是这样的写法：参数名字在前，然后:隔开，然后参数类型在后。
4、 Scala不需要显式地使用return关键字表示返回值。

另外，Scala的函数内部还可以定义函数，就像这样：

def main(args: Array[String]): Unit = {
  def inner(): Unit ={
    print("...")
  }
}

我在main函数内定义了一个内部的函数inner，并且可以（且仅在）main函数内部使用。而在 Java中，我们是不能这么做的。

Scala函数可以具备默认参数

我们可以在定义函数的时候直接在后面使用=号赋一个默认值。

def greet(word : String = "Scala"): Unit ={
  println(s"Hello,$word!")
}
//---Main---//
greet()

这样，即便在调用greet函数的时候，即便我们不显式传入参数，greet()仍然能够打印出：Hello,Scala!

但是我们如果这么做的话，下面代码就会报错了。

def greet(word1 : String = "Scala", word2 : String): Unit ={
  println(s"$word1,$word2!")
}
//----Main-----//
greet("hello")

究其原因是因为：编译器并不确定这个”hello”究竟是要覆盖word1的默认赋值，还是要给word2赋值。而我们可能是希望：“让word1使用默认参数，而将“hello”字符串赋值给word2”。为了避免这样的误会，我们在赋值的时候需要显式地指定这个”hello”所赋予的变量。

//word1具有默认值，我们显式地声明将hello赋值给word2，此时就不会有问题了。
//屏幕会打印：Scala，Hello！
greet(word2 = "hello")

Scala中函数参数是val类型

字少，但很重要。因为这个特性，我们不能在函数内对参数的引用地址进行二次修改。

Scala函数中的可变参数

Java中的可变参数实际上是一个数组。

验证的方法是：在同一个类下复制下方的代码，并试图让其重载，但是编译不通过。说明编译器认为不定参与数组是同一类型。

注：重载只判断方法名，参数列表。与返回值和修饰符无关。

//Java中用...来表示可变参数。
public void numbers(int... Ints){
    for (int i:Ints) System.out.println(i);
}

//重载失败了，说明Java编译器认为这个函数的签名是一样的。
public void numbers(int[] Ints){
    for (int i:Ints) System.out.println(i);
}

另外，可以用数组来为不定参数赋值，但是反过来，不能用多个参量对一个数组参数赋值。

//可变参数类型
public static void numbers(int... Ints){
    for (int i:Ints) System.out.println(i);
}

//允许这样使用
int[] arr =  {1,2,3,5,6};
numbers(arr);
//------------------------------------------------------------------
//数组参数
public static void numbers(int[] Ints){
    for (int i:Ints) System.out.println(i);
}

//错误的使用
numbers(1,2,3,4,5);

另外，为了避免可变参数带来赋值混乱的问题，函数内有其它参量时，将不定参数放在最后赋值。

//正确的声明
public static void numbers(int a,int... Ints){}

//错误的声明
public static void numbers(int... Ints,int a){}

Scala中的不定参赋值方式与Java相同，不过写法有一些区分。在类型后面加一个*号，表示它是一个不定参数。

//Scala Type. 注意可变参数放在后面。
def numbers(int: Int, ints: Int*): Unit = {
  println(s"输入了${ints.length+1}个参量")
}

警惕这样的写法

//这个str是一个变量吗?
def str = "This is a String."

上面代码的str是字符串吗？并不是。只不过由于它是一个只返回字符串的简单函数，因此省略了{}部分。又由于该函数不需要参数，所以连()部分都省略掉了。

当我们调用str的时候，似乎忽略了一些细节？是的。在这里str究竟是一个字符串，还是一个被包装的方法？Anyway，我们似乎不那么关心了：我们只知道调用str就能获得一个字符串。

以至于我们再做的复杂一点：

def str = {

  var temp =   "this is a string."

  temp + "(but not actually)"

  temp + "well, but they don't know the detail~"

  temp
}

//----而对于代码的调用者而言，它并不知道str其实是经过复杂的处理得到的。-----//
println(str)

而在用户看来，str好像还是一个字符串。没错，这就是无参数函数所造成的一个神奇的幻觉。但它的初衷并不是为了迷惑大众，而是与统一访问原则（uniform access principle）有关。笔者会在函数高级部分详细地介绍这个原则，以及空括号函数，无参数函数的具体使用细节。

惰性函数

假如不打算开火,就别让一支上膛的来福枪出现。这一理论被称为“契诃夫之枪”。

惰性计算是许多函数式编程语言的特性（如Spark的延迟调用例子）。它使得耗时的计算推迟到绝对需要的时候才会进行。虽被冠以“惰性”两字，但在现实应用中，这种做法避免了加载许多庞大却又不会被使用的程序/文件，提高了系统的运作效率。

生活中一个惰性调用的例子：只有在用到水的时候才会打开水龙头，水会随之流下来；在不用水的时候，水龙头是关闭的，自然就不会产生水流。

再联想一个Java的懒汉式单例：假如有一个学生（笔者），只有在临近上交的时候他才会写作业：

/**
 * He is a lazy and cunning student.
 */
public class Student {
    private String Homework = null;
    public String handOn(){
        if(Homework ==null)
        {
            Homework = "I barely finished it on time ;)";
            return Homework;
        }
        return Homework;
    }
}

用一个简单案例来试探Scala的延迟加载

首先，定义一个普通的变量string，借助getString方法进行赋值。随后主函数打印一行”print a line”。我们在getString方法内留下一行打印命令做标记，这样就可以观察到程序真实的执行顺序了。

def main(args: Array[String]): Unit = {
  val string :String = getString
  println("print a line.")
}

def getString:String={
  println("This variable has been assigned.")
  "I'm a lazy boy"
}

控制台会打印两行语句：

This variable has been assigned.
print a line.

实际上我们并没有使用到string变量，但是主函数仍然按部就班地调用了getString方法并初始化了它。我们这时候希望：如果用不到string变量，主函数就干脆不加载它。此时，在该变量前加一个lazy关键字，表明它的初始化工作被推迟到了只有在被调用的那一刻才会进行。

lazy val string :String = getString

再一次执行执行程序，可以发现，由于string没有被使用，因此getString也没有执行。

print a line.

那按照下面的次序来执行程序，string就会预先加载吗?

lazy val string :String = getString
println("print a line.")
println(s"$string")

答案是否定的。注意：lazy标注的string只有在被调用的那一刻才会进行初始化。因此是先打印了”print a line”之后，getString才会被调用。

lazy也适用于变量声明

lazy同样也可以用在val类型的变量上（换句话说，lazy不能用在var类型的变量上）。其作用是一样的：只在必要的时候才会初始化它。

递归函数

函数嵌套调用的流程

比如说有一个嵌套调用的过程（下面是伪代码）：

fun1 ={
    fun2
}

fun2 = {
    fun3
}

fun3 = {
    return value
}
------main--------
call fun1

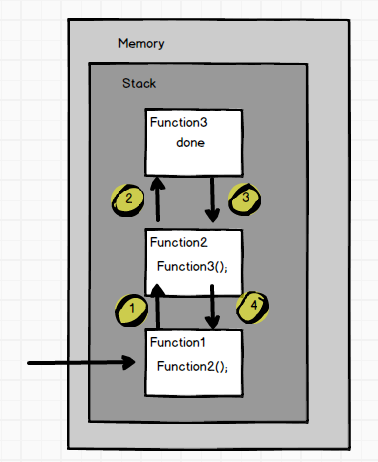
在执行fun1时，内存会开辟一个新的数据空间供fun1使用。但是由于fun1又需要fun2的返回结果，因此在这里会设立一个间断点，再为fun2开辟一个新的数据空间，并进入到该空间中（因为要执行完fun2才能继续执行fun1）。而fun2又需要fun3的返回结果，因此又设立了一个间断点，PC指向了为fun3开辟的新的数据空间中（因为要执行完fun3才能继续执行fun2）。

当fun3执行完毕时，fun2得到返回值，回到了原间断点处，继续执行，计算出结果返回给fun1。当fun1等到了fun2的返回值时，它也会从间断点处继续运行….

整体的运作流程都在一个栈空间内执行。即FILO的思想。

所谓递归函数的执行过程，就是设立一个中断条件，让fun1函数不断创建一个新的fun1函数进行计算，直到有一次fun1满足了中断条件，然后再将计算结果沿反向一路返回的过程。这个中断条件决定了递归函数的执行次数。因此如果该条件设立不当，递归函数将进行死循环，直到不断开辟的数据空间溢出内存。

当一个函数执行完毕，或者返回值，那么这个函数会执行完毕，程序指针回退到调用该函数的上一个函数的中断位置继续执行。

如果递归函数的参数是一个对象

若在递归函数传入了对象，递归改变的是对象内的成员，则情况又会发生些许的变化。为了说明这个问题，在此用Java代码来说明。

在这里声明了一个简单的主函数，递归函数，一个简单类。如果执行这个主函数，则屏幕上打印的会是0，1，2，3….10吗，或者是10，9，8，7….0？

public static void main(String[] args) {
    Counter counter = new Counter();
    cycRef(counter);
}
static void cycRef(Counter counter) {

    if (counter.count < 10) {
        counter.count += 1;
        cycRef(counter);
    }
    System.out.println("count =" + counter.count);
}
class Counter {
    int count = 0;
}

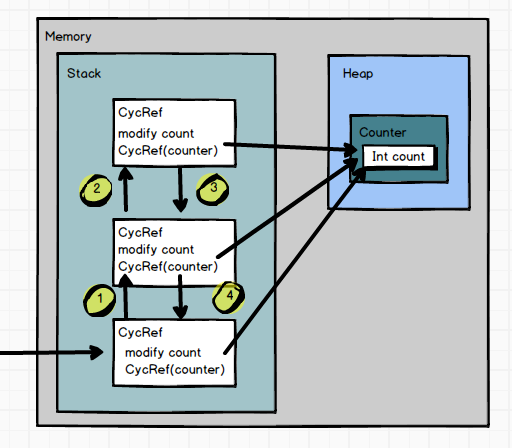
但结果是：它打印了11次10。

为什么会是这个样子呢？最主要的一点是，Java将这个对象放到了堆空间中，递归函数传递的是该参量所引用的对象在堆中地址值的拷贝（注意说法，仍然是值传递）。所以实际上这11个（算上主函数的调用，这个CycRef执行了11次）CycRef操作的Counter.count都指向Java堆内的同一个空间。当第11层嵌套的CycRef将Counter.count修改为10之后，回到第10，9，8….直到最外层的CycRef来看，Counter.count也同样是10，不会改变。

而假设我们进行递归的是一个基本数据类型，并运行它：

public static void main(String[] args) {
    cycVal(0);
}
static void cycVal(int counter) {
    if (counter < 10) {
        cycVal(counter + 1);
    }
    System.out.println("count =" + counter);
}

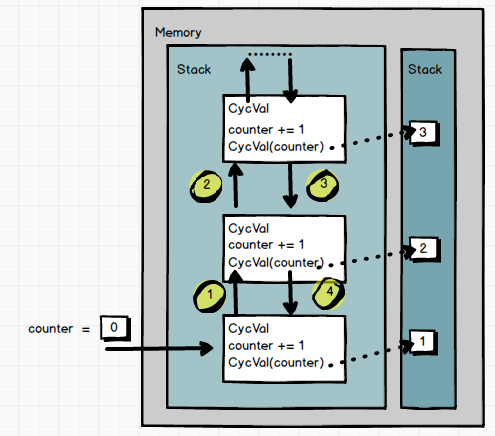
我们输出了10，9，8，7…..0。原因是由于参数是基本数据类型，因此每次调用CycVal的时候都传递的是字面值的拷贝，这个拷贝传递给了下一个CycVal方法接收并修改。因此每层CycVal都只会将自己得到的counter值做修改并输出，不会受其它的CycVal方法的影响。

注：Scala的AnyVal类型（比如Int,Double）也被认为是基本数据类型（尽管它也属于”类“的范畴），因此上述代码改写在Scala环境下并运行，结果是一样的。

顺带一提：Java的参数传递统统都是值传递。详情可以参考这个知乎链接：

使用递归函数的时机

只需要记住递归函数的两大基本要素：

1、 临界条件。如：设递归函数f(n)。当n=a时，有明确的返回值，或者程序终止。
2、 递归方程。如：f(n-1) = g(f(n))。等式两边都具有f(·)。

还有一个重要的条件：每次递归的方向应向着递归条件靠拢。我们都知道这个for循环将无穷无尽：

for(int i =1; i< 100; i --)。因为i会越来越小，这只会使得离循环结束的条件越来越远。

如果我们能快速地用数学公式概括出某个问题的的临界条件和递归方程，那么我们就可以使用递归来优雅地解决掉它。

简单的Scala递归函数练习

几个实例作为练习，使用Scala代码去实现。

1、计算n!（n的阶乘）。设f(n)= n * (n-1) * (n-2)... *(1)。。

我们简单分析就可以得知：f(0) =f(1) = 1(阶乘规定0的阶乘为1，此乃临界条件)；而阶乘有一条规律，即：f(n) = n* f(n-1)（递归方程），递归方向是沿着n减小的方向进行。（逼近临界条件）

//Scala是允许特殊符号作为命名的。参考Scala数据格式 & 命名
//设!!(n) = n * (n-1) * ... * 1
def !!(n: Int): Int = {
  //n=1,n=0可以简化成n<3
  if (n < 3) {
    1
  } else{
    //!!(n) = n * !!(n-1)
    n * !!(n-1)
  }
}

2、斐波那契(Fibonacci)数列问题：百科上有很多关于该数列的阐述与说明，在这里略。

我们能得到以下有用的信息：F(1)=1,F(2)=2(临界条件)，F(n)=F(n-1) + F(n-2)(递归公式)；递归方向为n从大到小递归（逼近临界条件）。

//F(n) = F(n-1) + F(n-2)
//F(1) = 1 ; F(2) = 2
def Fibonacci(int: Int): Int = {
  //当int=1时返回1，当int=2时返回2，这里做了简化。
  if (int < 3) {
    int
  } else {
    Fibonacci(int - 1) + Fibonacci(int - 2)
  }
}

3、猴子吃桃问题：猴子第一天摘下若干个桃子，当即吃了一半，还不过瘾，又多吃了一个。第二天早上又将剩下的桃子吃掉一半，又多吃了一个。以后每天早上都吃前一天剩下的一半零一个。到第10天早上想再吃时，见只剩下一个桃子了。求第一天共摘多少个桃子？

这是一个应用题，需要将题目条件抽象成递归函数的要素。桃子的数量跟天数有关，因此将天数设置为变量n，这个关系设为f，则每天的桃子数量可表示为f(x)。

从第一个灰色标注的句子中我们能推断出： ? F(n+1) = \frac{F(n)}{2} + 1 ? 或者反过来理解（我们以它为递归方程）： ? F(n) = 2(F(n+1)-1) ? 我们从题目中判断出来了：F(10) = 1，表示第10天只有1个桃子。(临界条件)。递归方向是n从1到10递归。

//f(n + 1) = f(n) / 2 - 1
//f(n) = 2(f(n+1) + 1)
def peach(int: Int): Int = {
  if (int == 10) {
    1
  } else {
    2 * (peach(int + 1) + 1)
  }
}
//-----Main--------//
println(s"${peach(1)}")

最终我们会得到答案为：1534个。

递归函数的大忌：重复计算

我们再来看看刚才的斐波那契数列运算：

//F(n) = F(n-1) + F(n-2)
//F(1) = 1 ; F(2) = 2
def Fibonacci(int: Int): Int = {
  //当int=1时返回1，当int=2时返回2，这里做了简化。
  if (int < 3) {
    int
  } else {
    Fibonacci(int - 1) + Fibonacci(int - 2)
  }
}

这个解决方案从效率上说并不好：原因是下面这一行代码包含了大量的重复运算：

Fibonacci(int - 1) + Fibonacci(int - 2)

程序首先会进入到第一个Fibonacci中进行递归，之后再进入第二个Fibonacci进行递归。可实际上这两个递归99%的计算过程都是重复的。这导致这个递归函数的复杂度成指数倍增长，大量的时间被浪费在了重复的计算上：当int=40的时候，这个程序就已经相当于死循环了。

但是递归求阶乘的过程中，就没有进行重复运算，因此即便n传入了相当大的数（需要把Int更改为BigInt），程序通过递归也能相当快速地求出解。

感兴趣的同学可以亲自实现代码，并比较Fibonacci(50)和阶乘(50)所需要的运算时间。同时也有很多大牛对Fibonacci问题给出了优化方案，在这里不展开细谈。

递归方式找到ListBuffer中的最大值

这个例子是笔者在后续的集合学习中所补充的一个案例。笔者还需要一段时间才能更新到Scala集合的部分。

这个递归方程和临界条件就不那么好用式子来形容了。因此我们首先要整理思路：

首先，将这个序列中的head设置为最大值。然后和tail子集（tail指去掉首元素head后，剩下的元素重新组成的集合）中的最大值相比较。如果确实是第一个元素最大，则返回head。另外，我们同样使用递归方法来搜索tail子集内的最大值。
如果head不是实际的最大值，则将这个head去掉，再去剩下的tail子集当中找最大值，重新第一步的步骤。

除此之外，我们再额外补充上list的长度为0和为1的特殊情况，并给出以下代码：

def max(listBuffer: ListBuffer[Int]):Int={

    if(listBuffer.isEmpty) ()

    if(listBuffer.size == 1){
      listBuffer.head
    }

    else if(listBuffer.head > max(listBuffer.tail))
    {
      listBuffer.head
    }else max(listBuffer.tail)
}

平时我们所遇到的大部分应用问题，好像都很难用数学公式概括出它的临界条件和递归方程。因此，除非递归的思路非常清晰，且保证该递归方法没有进行低效率的重复运算，在一般情况下笔者还是会选择使用传统的循环分支来解决问题。

文章永久链接：https://tech.souyunku.com/41965

Scala之：FP与OOP && 函数初级