了解快速排序
快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略,通常称其为分治法(Divide-and-ConquerMethod)。快速排序是一种不稳定的排序法。
快速排序的操作步骤
1、 取出一个数作为基准。(下文将该基准命名为temp)
2、 所有小数在其前,所有大数在其后,因此temp左右两边共产生了两个子区间。
3、 两个子区间内部未必是有序的。因此分别在每个区间内重复1,2操作,直到各个区间只有一个数。禁止套娃?
由于每个区间内的处理方法是重复的,因此我们可以用递归函数来实现它(递归函数占用栈空间),也可以采取while循环来解决。
快速排序可以轻松应付庞大且无序的数组,但是若用于高度有序(甚至完全升序,降序排列好的,元素内容完全重复的)的数组,表现反而会很糟糕。
挖坑法提供的解决思路
上段中提到的操作步骤2有很多种方法实现,思路大同小异。在这里使用挖坑法来实现。 我们首先准备:
- 两个”指针” (虽然它们实际上只是数组下标号,但为了方便理解,下文仍统称为指针)
low和high,分别指向数组的首和尾,且high只向左移动,low只向右移动。 - 默认将数组首元素保存到
temp当中。
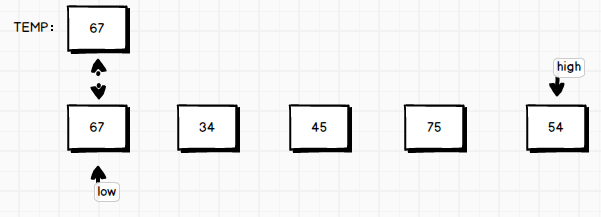
换个说法,在程序开始前,在arr[low]的位置挖了坑,该位置上的数被移到了temp中。
有一个大前提:在调用该函数时low < high必须成立,否则不再继续递归。因为low==high意味着这个数组只有1个元素,那就没有必须再进行排序了。
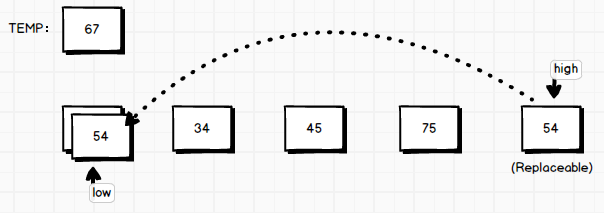
程序运行,low指针不动,而high指针判断它所目前指向的值是否大于temp。满足条件则左移,否则high指针会停下来,将当前指向的值覆盖到arr[low]位置上。(演示图里第一次判断就中了奖 =D)
或者说,
high位置上的数被挖出来填到了low位置上的坑。
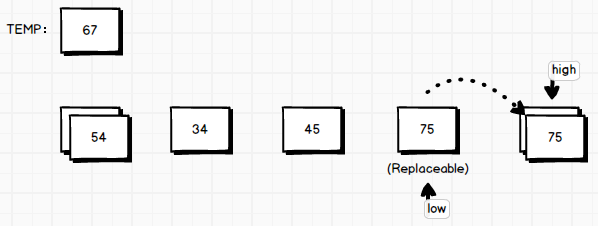
high指针不动, low指针判断它所目前指向的值是否小于 temp。满足条件则右移,否则 low指针会停下来,将当前指向的值覆盖到 arr[high]位置上。(这一段叙述和上一段叙述互为反过程。)
或者说,
low位置上的数又被挖出来填了上一步high指针位置留下来的坑。
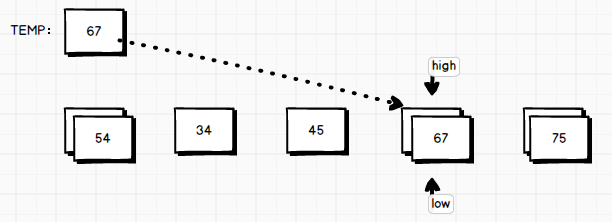
high指针再次开始左移,直到发现大于等于temp的数,则将其挖出来填到low指针的地方并暂停,随后low指针又不断右移,直到发现小于temp的数,再将它挖出填到high指针处……high和low指针一直处于交替相向移动的状态。
如此下去,总有一刻high指针和low指针会指向同一位置。此刻无需再移动high和low指针,只需要把最初挖出来的temp值,放到这个坑内即可。
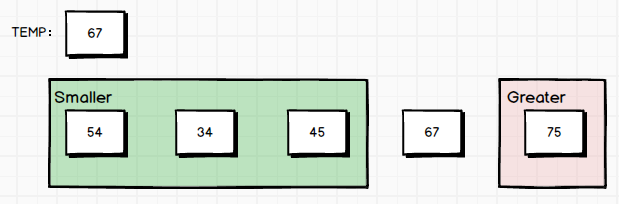
我们此时可以发现,原先的数组已经被分为了三部分:比temp小的数,temp,比temp大(或等)的数组。
只需要再对Smaller和Greater区间进行递归操作,重复之前所述的步骤就可以了。
基于挖坑法的Java快速排序
static void quickSortJ(Integer[] arr, int start, int end) {
if (start < end) {
Integer low = start;
Integer high = end;
Integer temp = arr[low];
while (low < high) {
while (high > low && arr[high] >= temp) high--;
if (high > low) arr[low] = arr[high];
while (high > low && arr[low] < temp) low++;
if (high > low) arr[high] = arr[low];
}
arr[high] = temp;
quickSortJ(arr, start, low - 1);
quickSortJ(arr, high + 1, end);
}
}
我只要[Smaller[], Temp, Greater[]]!
我们在进行一轮排序后(左右指针法,挖坑法,etc.)必定能将数组分割成以下形式:[Smaller[], temp, Greater[]]。那能不能用更简单偷懒的方法来得到Smaller区间和Greater区间呢? 在Scala中,可以直接利用过滤器filter来过滤出比temp小(或大)的数。如:
arr.filter(x => x > temp) //filter处理之后得到的仍是Array[],放心食用。
而后再对过滤出来的Smaller[],和Greater[]继续进行递归即可。用Java的流处理同样可以实现类似逻辑,但是比较麻烦。
用Scala实现快速排序
def quickSortScl(arr: Array[Int]): Array[Int] = {
if (arr.length <= 1)
arr
else {
//这里的temp没有选取首元素,而是取中间元素.
val temp =arr(arr.length/2)
//返回一个[SmallerThanTemp[],temp,GreaterThanTemp[]].
Array.concat(
quickSortScl(arr.filter(x => x<temp)),
//如果有多个相等的元素,则该数组内的元素个数大于1.
arr.filter(x => x==temp),
quickSortScl(arr.filter(x => x>temp))
)
}
}