
思路:动态规划
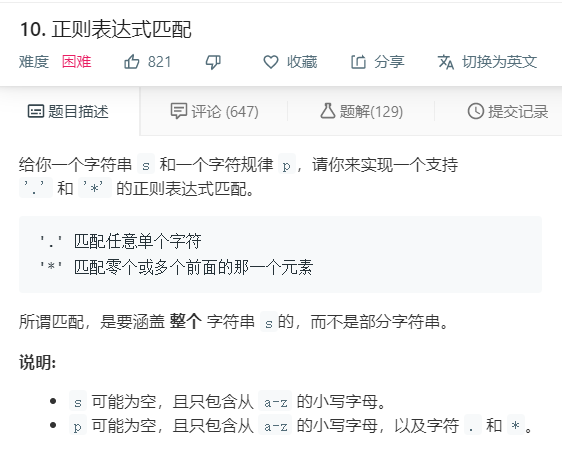
- 这是一个通配符问题
- .表示任意字符,*表示0个或多个字符,.*表示任何字符串除null外
- 理解.*匹配ab, .*可以匹配..,每个点可以匹配任意字符,所以.*匹配ab
- 通过动态规划来解决
- dp[i+1][j+1]表示s中长度为i的子串与p中长度为j的子串是否匹配,这里s中长度为i的子串表示s.substring(0, i)
- dp的长度 s.length + 1,p.length + 1
- dp[0][0] = true,表示空串肯定匹配空串
- 参考:www.youtube.com/watch?v=c5v…
- 参考:www.youtube.com/watch?v=ym1…
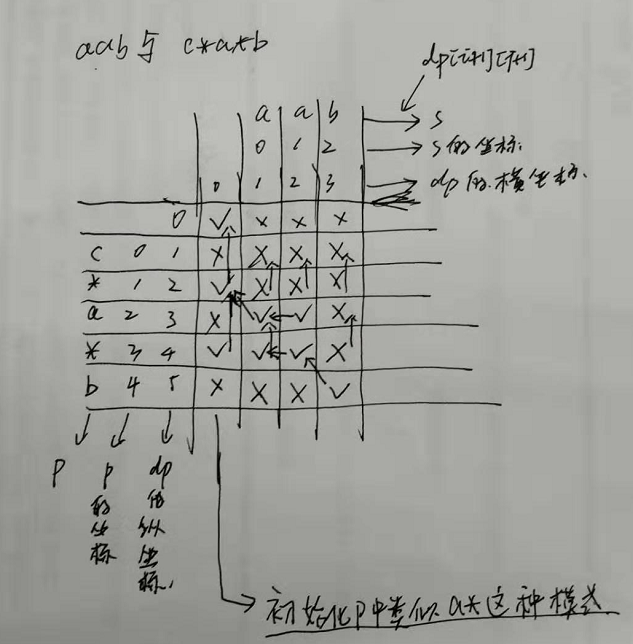
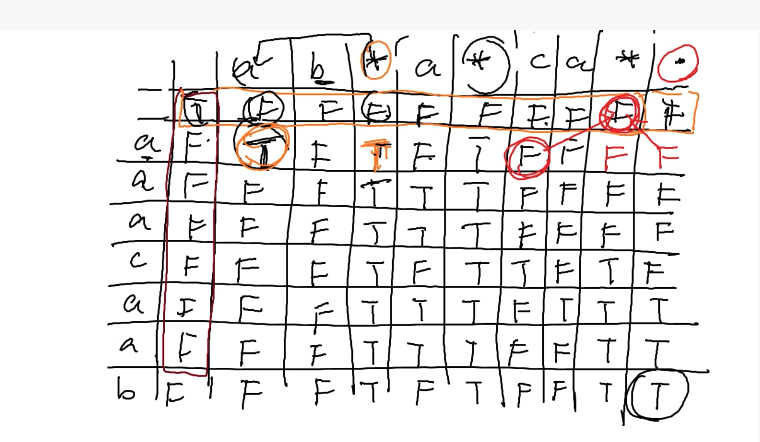
这个是参考视频的画的图例
public boolean isMatch(String s, String p) {
// 字符串为空返回false
if (s == null || p == null) {
return false;
}
boolean[][] dp = new boolean[s.length() + 1][p.length() + 1];
// 这种情况s="",p=""返回true
dp[0][0] = true;
// 初始化p中类似a*这种模式
for (int j = 0; j < p.length(); j++) {
if (p.charAt(j) == '*' && dp[0][j - 1]) {
dp[0][j + 1] = true;
}
}
for (int i = 0; i < s.length(); i++) {
for (int j = 0; j < p.length(); j++) {
if (p.charAt(j) == s.charAt(i) || p.charAt(j) == '.') {
dp[i + 1][j + 1] = dp[i][j];
}
if (p.charAt(j) == '*') {
// a*匹配空串
if (p.charAt(j - 1) != '.' && p.charAt(j - 1) != s.charAt(i)) {
dp[i + 1][j + 1] = dp[i + 1][j - 1];
} else {
// a*,可匹配 a,aa
// .*,可匹配 任意子串
dp[i + 1][j + 1] = dp[i + 1][j - 1] || dp[i + 1][j] || dp[i][j + 1];
}
}
}
}
return dp[s.length()][p.length()];
}