前言 :本来只是想简单记录一下,没想到好像学到了什么了不得的东西OvO
太长不看版
真值与机器数
在计算机中,我们使用 0 表示正数,1 表示负数。将最高位作为符号位,使用 0 或 1 表示正负的二进制数称为机器数,而原来的数称为真值。
比如,如果我们有机器数 x = 01101,y = 10110,则其对应的真值分别为 x = +1101,y = -0110。
需要注意的是,二进制的位数是受机器设备的限制的。机器内部设备一次能表示的二进制位数叫做机器的字长,一台机器的字长是固定的。字长 8 位叫一个字节 ( byte ),机器字长一般都是字节的整数倍,如字长 8 位,16 位,32 位,64 位等等。
原码、反码,与补码
原码、补码、反码是机器数的三种表现形式。
原码
将数的真值形式中的 ” + ” 用 0 表示,” – ” 用 1 表示时,叫做数的原码形式,简称原码。
由此,当以机器字长为 4 位时为例,我们可以列出如下对应关系 :
| 正数 | 负数 | ||
|---|---|---|---|
| 0 | 0000 | -0 | 1000 |
| 1 | 0001 | -1 | 1001 |
| 2 | 0010 | -2 | 1010 |
| 3 | 0011 | -3 | 1011 |
| 4 | 0100 | -4 | 1100 |
| 5 | 0101 | -5 | 1101 |
| 6 | 0110 | -6 | 1110 |
| 7 | 0111 | -7 | 1111 |
原码的表示法比较直观,它的数值部分就是该数的绝对值,并且与真值、十进制的转换十分方便。但依然存在着一个问题 :当两数相加时,机器需要首先判断两数的符号是否相同,若相同,则绝对值相加,若不同,则绝对值相减。并且,在做减法之前,还需要判断两数绝对值的大小,然后用大数减去小数,最后再确定差的符号。
换言之,当使用原码这样一种直接的形式进行加运算时,负数的符号位不能与其数值部分一同参与运算,而必须为其设置额外的逻辑去处理,这就造成了麻烦。由此,引入了反码与补码的概念。
反码
反码的表示方法 :
- 若机器数为正数,则反码与原码一致
- 若机器数为负数,则反码是在原码基础上保持其符号位不变,其他位置取反
| 正数 | 原码 | 补码 | 负数 | 原码 | 补码 |
|---|---|---|---|---|---|
| 0 | 0000 | 0000 | -0 | 1000 | 1111 |
| 1 | 0001 | 0001 | -1 | 1001 | 1110 |
| 2 | 0010 | 0010 | -2 | 1010 | 1101 |
| 3 | 0011 | 0011 | -3 | 1011 | 1100 |
| 4 | 0100 | 0100 | -4 | 1100 | 1011 |
| 5 | 0101 | 0101 | -5 | 1101 | 1010 |
| 6 | 0110 | 0110 | -6 | 1110 | 1001 |
| 7 | 0111 | 0111 | -7 | 1111 | 1000 |
补码
补码的表示方法 :
- 若机器数为正数,则补码与原码一致
- 若机器数为负数,则补码是在反码的基础上加1,并舍弃溢出位
| 正数 | 原码 | 反码 | 负数 | 原码 | 补码 | 反码 |
|---|---|---|---|---|---|---|
| 0 | 0000 | 0000 | -0 | 1000 | 1111 | 0000 |
| 1 | 0001 | 0001 | -1 | 1001 | 1110 | 1111 |
| 2 | 0010 | 0010 | -2 | 1010 | 1101 | 1110 |
| 3 | 0011 | 0011 | -3 | 1011 | 1100 | 1101 |
| 4 | 0100 | 0100 | -4 | 1100 | 1011 | 1100 |
| 5 | 0101 | 0101 | -5 | 1101 | 1010 | 1011 |
| 6 | 0110 | 0110 | -6 | 1110 | 1001 | 1010 |
| 7 | 0111 | 0111 | -7 | 1111 | 1000 | 1001 |
| -8 | 1000 |
值得注意的是,补码解决了原码与反码中“ 同时存在 +0 和 -0 ”的问题,从而使整个存储多出来一个位置。正是因为机器使用补码,所以对于编程中常用到的 32 位 int 类型,可以表示的范围为 [-2^31, 2^31 - 1]。其第一位为符号位,而使用补码时又可以多保存一个最小值。
写在后面
下面是一点解释和碎碎念。
模
首先需要理解的是“ 模 ”的概念。
还是拿经典的时钟表盘举例子,首先我们有一个钟表,它指向 4 点 :
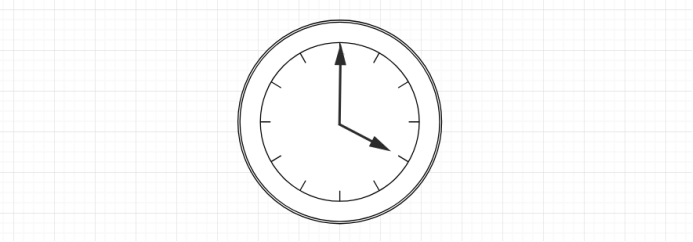
如果我们要把指针拨到 “ 10 小时之后的时间点”,可以怎么做呢?一种方式是将指针向前(顺时针)拨 10 个单位,而另一种方式,则是将指针向后(逆时针)拨 2 个单位。
对于容量为 12 的时针来说, +10 和 -2 得到的结果是一致的。也即是说,虽然 4+10 这一运算超出了预设的位数 12,从而造成了溢出,但我们直接舍弃掉溢出的部分,依然能够得到正确的结果。
这里的 “12” 即是该计数体系的 模。在这个有限容量的计数体系中,对于一个已知的数值 X ,在其的基础上 +10 和 -2 是完全相同的,故称 -2 和 +10 是关于模 12 的一组补数。这种将 X-2 转化为 X+(模-2) 的运算方式,正是计算机 “化减为加” 的基础。
因此,我们在有限的计数系统中做出了这种定义 :正数的补数为其本身,负数的补数 = 模 – 该负数的绝对值。一个数加上另一个数(不论正负),结果等于加上这个数的补数。如果在此过程中发生溢出,相加得到的数值超出了计数体系的最大容量,就可以像多转了一圈的指针一样,直接舍弃溢出的这一部分,而不会对结果的正确性产生影响。
符号位
在 8 位计算机中,一个字节可以表示 256 种状态。如果把字节看做一个钟,将分界点 -128 和 0 分别标在原表盘 12 点和 6 点所指的位置。当计算 120 D + 120 D 时,我们在 120 的基础上指针顺时针拨 120 个单位,当指针掠过 -128 这一分界点,数值由正数变为了负数,最终指向 -16 的位置。
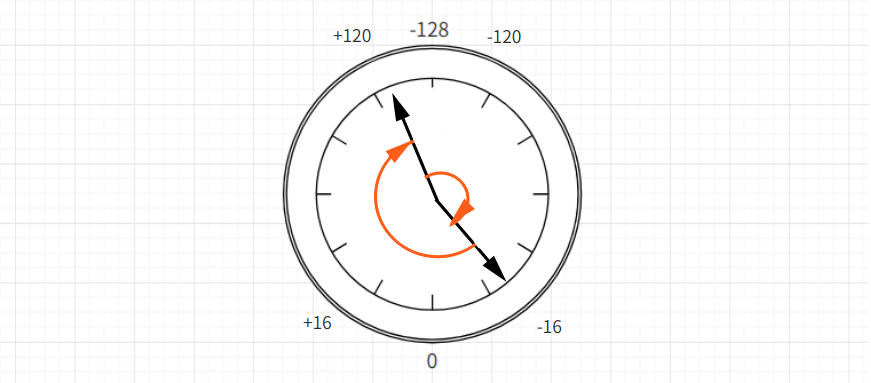
这个时候再来查看二进制的计算方式,120 D + 120 D = 0111 1000 B + 0111 1000 B = 1111 0000 B,最高位接受来自地位的进位,说明该计算越过了 “分界点”,需要求其补数来得到正确结果。对 1111 0000 B 求补得到 1001 0000 B,即 -16 D,和上述推理一致。
引用 @张天行 的总结,“加法都是从地位往高位做的,如果两个数(补码)后七位相加产生了进位,说明发生了溢出。每当溢出一次,符号就要反一下,0 变 1,1 变 0。符号是 1 的,说明大得越界了,需要再求个补,用取值范围内的负数表示结果;符号是 0 的,说明小的越界了,但由于正数的补数就是本身,就不必再求补了。”
这是数学的自洽与和谐,令人兴奋的自然之美。这一点点内容断断续续拖了几天,期间拜读了好几位大神的回答,可能有点莫名其妙,但不知为何每一遍都让人心潮澎湃。不是由于规定了符号位,所以用最高位的 1 和 0 来表示正负,而是因为补码运算可以通过最高位来表示正负,所以符号位诞生了。补码它就在那里,并非被定义或发明;我们 “发现”了它。