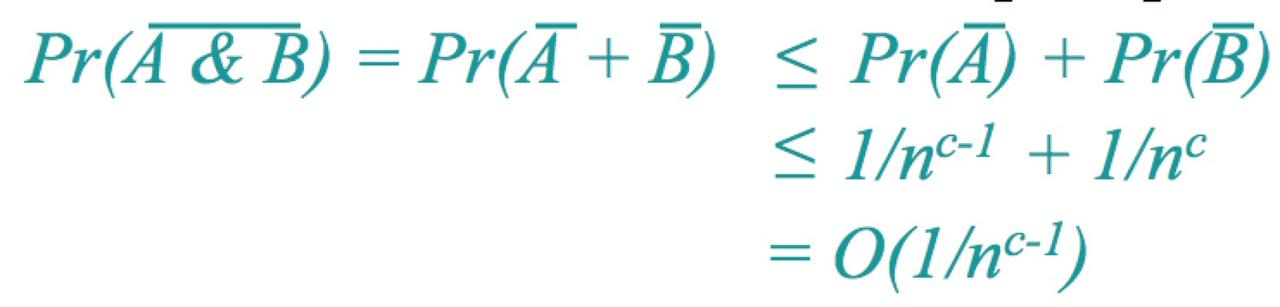zadd用来往有序集合中添加值
> zadd count 1 paxi 2 maokitty
(integer) 2
zadd语法为 zadd key [nx|xx] [ch] [incr] score member ,详情戳我
通过 zrank 可以找到key对应的排序
> zrank count paxi
0
其中0表示它是当前排序集合里面分数最小的。 在redis的底层实现中，就用到了skiplist作为实现排序集合的数据结构
SkipList的基本性质
它维护了n个元素的动态集合，有很大的可能性，每个操作的时间花销是O(lgn)
如何加速一个有序链表的搜索速度
对于上面链表的搜索，最差情况下是要全部搜索一遍，时间花销是O(n)。
再造一个有序的链表，它有指向第一个列表的指针，并从第一个列表中复制部分的值，详情如下
对上述的结构搜索，它的步骤如下：
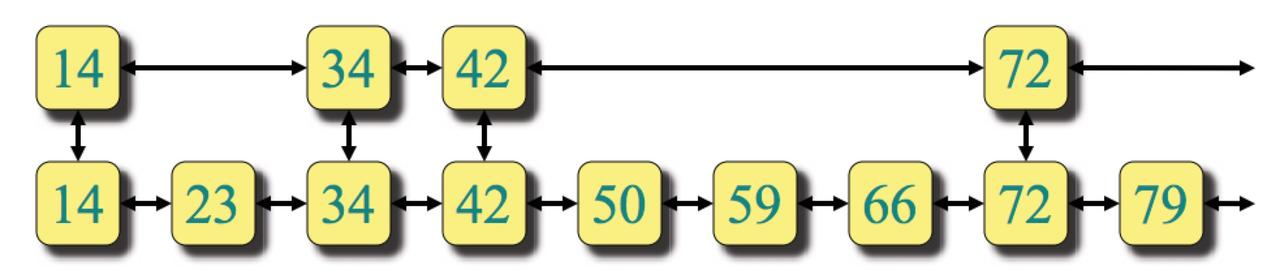
- 先从顶层开始查找，直到要找的值比当前查到的值要小;
比如要找66，在顶层查到42再往前查是72，比66要大，所以停在了42
- 从第一步中的位置往底层走。
比如第一步中停在了42，往下走仍然在底层的42上
- 从底层往右继续查找，知道找到元素或者这个元素根本不存在
命名顶层链表为L1，底层链表为L2，那么整个查找所需要的时间为
只会查找L2的一部分，假设均分100个元素为5份，那么底部最多找20个
要使得查询时间最小有 
，假设|L2|=n，那么可得查找时间为
。
实际上可以得到的是，2个list，得到的
,3个list得到的是
,3个list得到的是
,k个list得到的是
,那么lgn层得到的是
skiplist中的搜索与插入
理想情况下的skiplist它有lgn层
比如说要搜索 72 ，它的搜索路径为图中红色所示的部分，从上到下，从左到右
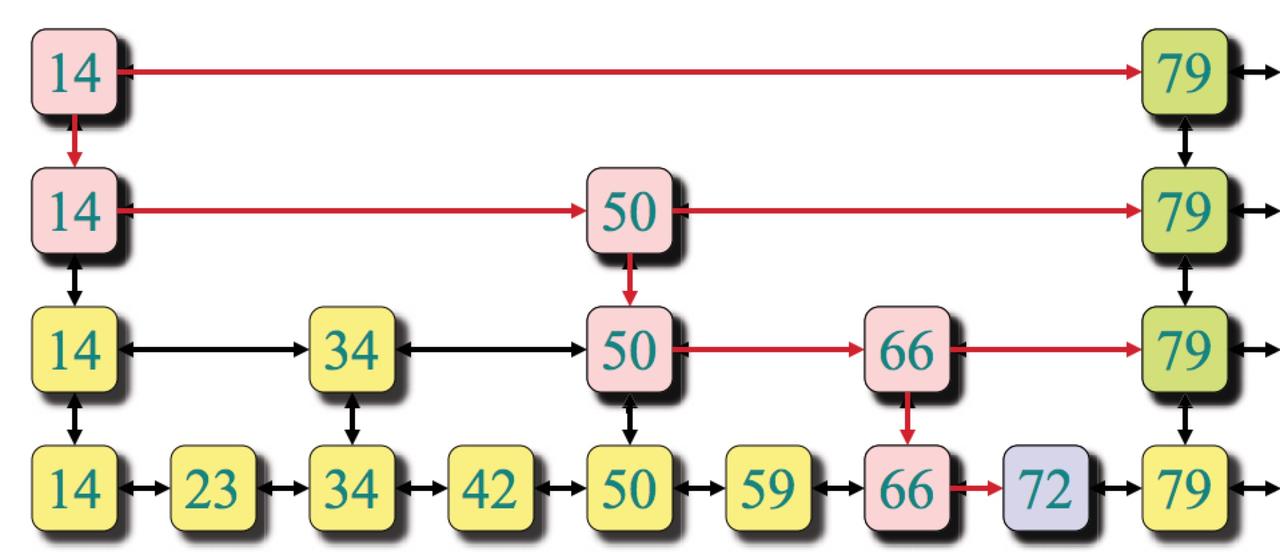
插入元素
在最底层的链表中，它维护了所有的元素，关键是，那个元素应该插入到上面的一层呢？理想情况下，解决方案是扔一个公平的硬币(正反的概率都是1/2)，如果扔到的是正面朝上，那么就让当前元素同时存储到上一层链表，那么平均来说，1/2的元素会存储到第二层，1/4的元素存储到第三层等等
证明
n个元素的skiplist有非常大的概率只有O(lgn)层
假设它会比lgn层要大:
这意味着至少存在一个元素需要往上存储的次数大于 clgn 次，而总原数是n个，也就是说这个概率必定小于所有元素都往上存储的并集
BOOLE 不等式：对于任意的事件 E1，E2，…，Ek 有
也就是说
另α=c-1,也就是说，层数超过 lgn的概率小于 
，当α很大的时候，概率就很小，所以可以使用 O(lgn)
在skiplist中搜索元素，有非常大的概率期望的搜索时间是O(lgn)
考虑已经找到了元素，现在开始回顾整个过程
- 找到的元素从底层开始
- 如果找到元素上面没有元素，那么往左回溯
- 如果找到的元素上面有元素，那么往上回溯
- 直到回溯到了最上一层
1、 这个过程中往上需要查找的次数肯定是小于等于总共的层数，而它有很大的可能性就是O(lgn)。
2、 对于总的移动的次数来讲，它的发生肯定是经过了 clgn 次的向上移动，它就等价于抛硬币的总次数，直到有 clgn 次都是正面朝上再停止，而这个事件发生的概率也就是O(lgn)
根据Chernoff Bounds，假设Y是代表在m次独立随机的抛硬币过程中出现head的次数，其中每次抛硬币获得head的概率是p,那么对于任意的r>0有：
E[Y]表示期望值，比如m次，概率p是1/2,那么E[Y]=m/2
根据Chernoff Bounds，可以得出对于任意一个c,一定存在一个d,使得抛硬币 dlgn 次，有很大的概率至少有 clgn 次硬币朝上
m=dlgn,p=1/2
综上可以得到两个事实：
1、 A：层数有很大的概率小于等与 clgn
2、 B：在获得 clgn 次向上移动的过程中，需要移动的次数有很大的概率小于等于 dlgn
要这两个同时发生Pr(A & B)有
redis中zadd过程源码分析
在执行zadd命令后，实际上根据当前key的数量和member的大小，会有不同的存储方式
if (server.zset_max_ziplist_entries == 0 ||
server.zset_max_ziplist_value < sdslen(c->argv[scoreidx+1]->ptr))
{
zobj = createZsetObject();
} else {
zobj = createZsetZiplistObject();
}
1、 使用zset结构
2、 使用zsetziplist结构，ziplist请戳我
zset的结构如下
typedef struct zset {
dict *dict;
zskiplist *zsl;
} zset;
在这个结构中使用的zskiplist结构如下
typedef struct zskiplist {
struct zskiplistNode *header, *tail;
unsigned long length;
int level;
} zskiplist;
链表中使用到的 zskiplistNode ,有如下定义
typedef struct zskiplistNode {
sds ele;
double score;
struct zskiplistNode *backward;
struct zskiplistLevel {
struct zskiplistNode *forward;
unsigned long span;
} level[];
} zskiplistNode;
当需要往skiplist中插入元素时，主要过程如下
Code.SLICE.source("x = zsl->header;")
.interpretation("拿到跳表的头节点");
Code.SLICE.source("for (i = zsl->level-1; i >= 0; i--) {" +
" /* store rank that is crossed to reach the insert position */" +
" rank[i] = i == (zsl->level-1) ? 0 : rank[i+1];" +
" while (x->level[i].forward &&" +
" (x->level[i].forward->score < score ||" +
" (x->level[i].forward->score == score &&" +
" sdscmp(x->level[i].forward->ele,ele) < 0)))" +
" {" +
" rank[i] += x->level[i].span;" +
" x = x->level[i].forward;" +
" }" +
" update[i] = x;" +
" }")
.interpretation("从跳表的最高层开始，1层1层的找需要插入的score对应的位置")
.interpretation("1: rank用来计算元素在排序列表中排的顺序，rank[i]表示新节点的前一个节点与每层距离头节点的跨度")
.interpretation("2: 只要当前节点的分数小于要插入节点的分数，并且当前节点的前头还有，那么就一直往前遍历，记录下来层级之间的跨度，和最后需要插入元素的节点的前一个节点")
.interpretation("3: 如果分数一模一样，则比较key,key值大，仍然往前遍历")
.interpretation("4: 注意最高层的下标是 level-1");
Code.SLICE.source("level = zslRandomLevel();")
.interpretation("随机产生层级");
Code.SLICE.source("if (level > zsl->level) {" +
" for (i = zsl->level; i < level; i++) {" +
" rank[i] = 0;" +
" update[i] = zsl->header;" +
" update[i]->level[i].span = zsl->length;" +
" }" +
" zsl->level = level;" +
" }")
.interpretation("如果产生的层级大于当前提跳表的最大层级，那么将当前层级置为最高的层级")
.interpretation("1: 在所有新增的层都记下头节点和跳表的长度");
Code.SLICE.source("x = zslCreateNode(level,score,ele);")
.interpretation("创建一个跳表的节点对象，作为需要新插入的节点");
Code.SLICE.source(" for (i = 0; i < level; i++) {" +
" x->level[i].forward = update[i]->level[i].forward;" +
" update[i]->level[i].forward = x;" +
"" +
" /* update span covered by update[i] as x is inserted here */" +
" x->level[i].span = update[i]->level[i].span - (rank[0] - rank[i]);" +
" update[i]->level[i].span = (rank[0] - rank[i]) + 1;" +
" }")
.interpretation("遍历新元素所在层以及它下面的所有层级，插入新的元素,由于下层是插入新元素，那么这些位置的跨度必然会使得原有跨度变成两半")
.interpretation("1: 在遍历的时候已经记下了下面每一层的插入位置的前一个节点，那么新的节点的下一个节点就是已经查找位置的下一个节点，而要插入位置的元素它的下一个节点，就是新插入的节点")
.interpretation("2：Rank[0]表示第一层的总共跨度，也就是新元素在跳表中的排序，rank[i]是新节点的前一个节点在每层距离头节点的跨度，在插入新元素之前，前后的总跨度是 update[i]->level[i].span ")
.interpretation("3: 假设原有节点的跨度是4，原有两个节点的位置分别是 1和4，假设新插入的位置是 3， rank[0]-rank[i]的值2，那么新节点的跨度就是 4-2=2（2表示新节点和新节点的下一个节点）,位置1的节点的跨度就是 4-2+1=3");
Code.SLICE.source("/* increment span for untouched levels */" +
" for (i = level; i < zsl->level; i++) {" +
" update[i]->level[i].span++;" +
" }")
.interpretation("在新插入层级之上的层级，它们下方由于都新插入了一个节点，那么跨度均加1即可");
Code.SLICE.source("x->backward = (update[0] == zsl->header) ? NULL : update[0];")
.interpretation("如果新插入节点的前一个接单是头节点，则不设置后向指针，否则设置后向指针为它的前一个节点")
.interpretation("1 这里可以看到头节点其实只是作为1个指针使用，并不参与存值");
Code.SLICE.source("if (x->level[0].forward)" +
" x->level[0].forward->backward = x;" +
" else" +
" zsl->tail = x;")
.interpretation("如果新节点前面仍然存在节点，那么新节点的前一个节点的后节点就是新节点本身,否则说明新节点就是尾结点")
.interpretation("1: 这里可以看出只有第一层才是双向的链表");
Code.SLICE.source("zsl->length++;" +
" return x;")
.interpretation("插入了新的节点x,那么跳表总长度加1，返回新建的节点即可");
更详细的源码分析可以看附录的完整源码追踪过程
redis中的skiplist总结
1、 如果节点不多，允许使用ziplist会直接使用ziplist,超过阈值使用跳表;
2、 每个跳表节点维护了层级结构，没有冗余的存储多余的key和score;只有最底下一层是双向链表;
3、 随机增长层级是通过random实现
附录
张铁蕾-Redis内部数据结构详解(6)——skiplist
书：redis的设计与实现
书：redis开发与运维
MIT算法课