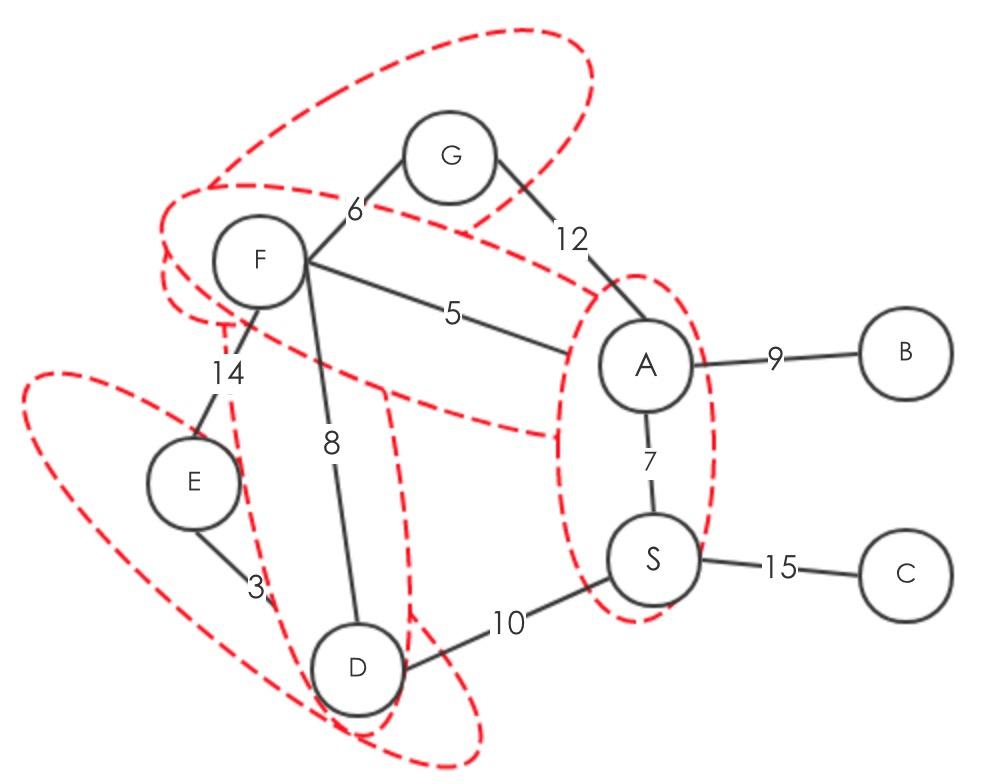
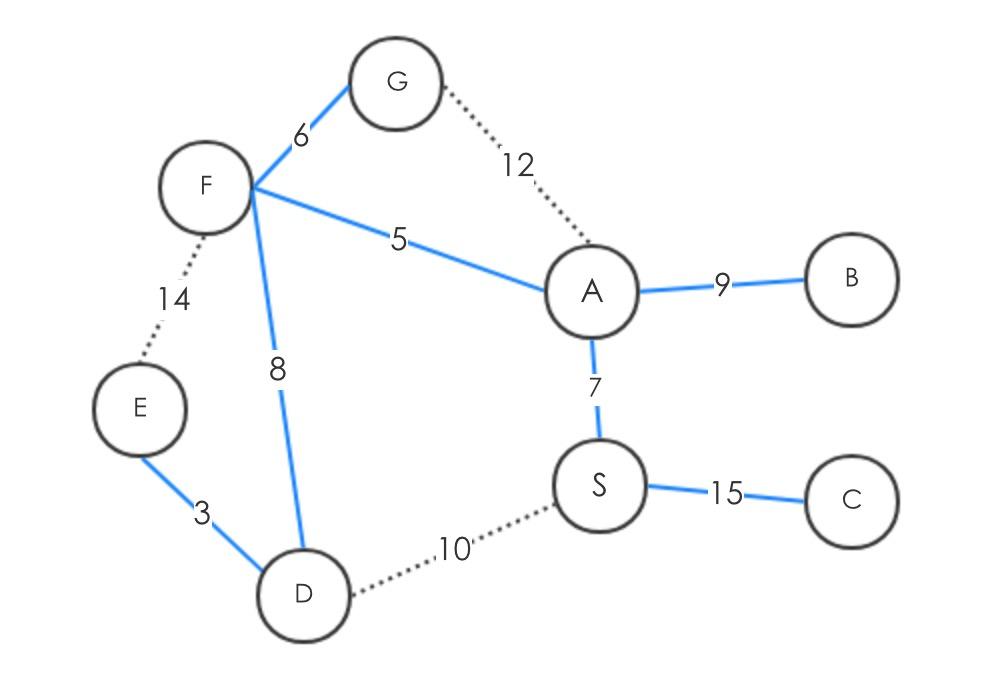
生成树的定义：对于一个图G，获取G的边使得所有的顶点都连接到。最小生成树(MST Minimun spanning tree):给定图G(V,E),以及对应的边的权重，获取一颗总权重最小的生成树。
树的定义:连接的无环图
直接策略
找到所有的生成树，然后计算权重最小的
考虑上面的图，一但红色线选定，对于接下了的标号为1,..,n的所有节点点，左右节点都只需要二选一即可得到不同的生成树，这样的选择有 
种，太多
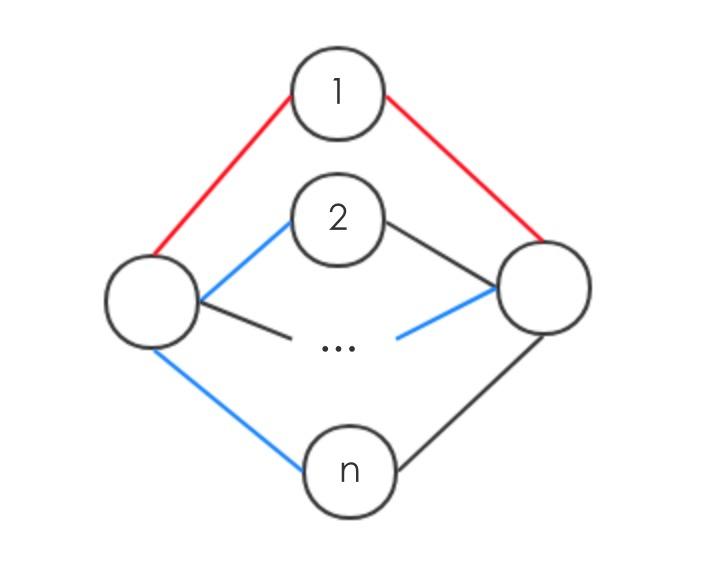
贪心算法的性质
1、 最优子结构:有多个子结构的最优解最终组成整个问题的最优解
2、 贪心算法的选择特定，会使得局部最优解最终也是全局最优解
寻找MST的最优子结构
假如边e={u,v}是某个MST的一条边，通过对合并这两个顶点为一个新的顶点(这种操作称作contract e)，将有多条边同时连接多个顶点的合并成一个权重最小的边保留，其它边的连接形式保持不变。可以证明假设T'是G/e(不包含e的G)的MST，那么T'U{e}也是G的MST
证明
假设T*(
)是G的MST，那么 T*/e（即T’） 也是 G/e的MST,即
而w(T’Ue)=w(T’)+w(e)，所以
因而成立
MST的贪心选择
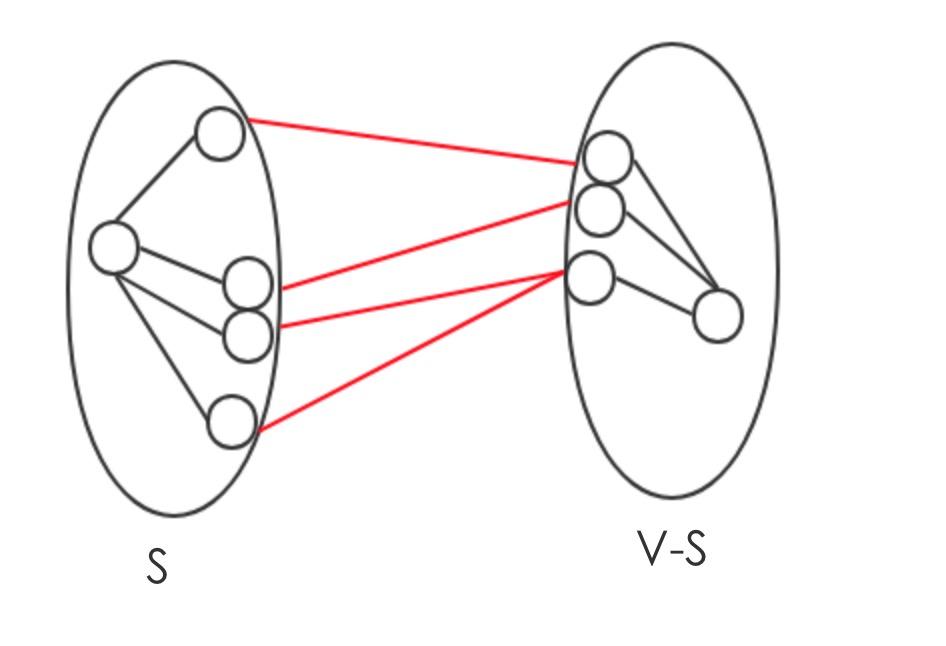
假设有任意的cut(S,V-S),选取e,使得e是所有crossing cut的最小权重的边
，那么e肯定是属于某个MST。
红色的线即 crossing cut的边
证明
假设T是G的一个MST，那么它必定存在一条边e’={u’,v’}横跨S和V/S，由于w(e)<=w(e’)，可以构造T’=T/{e’}U{e}=w(T)-w(e’)+w(e)<=w(T),也就是说T’也是MST，e属于某个MST。
Prim’s算法
维护一个优先级队列Q，它的节点u.key=min{w(u,v)|u in s and v in (S-V)}
- 随便选取单个节点作为S，其它的都是 S-V
- 在Q中存储V所有的节点，对于节点s,有s.key=0,其它的是 无穷大
- 只要Q中还有元素，获取最小的元素，遍历它的邻接表，如果节点v不在S里面，并且w(u,v)<v.key，更新v.key=w(u,v),记录v.parent=u
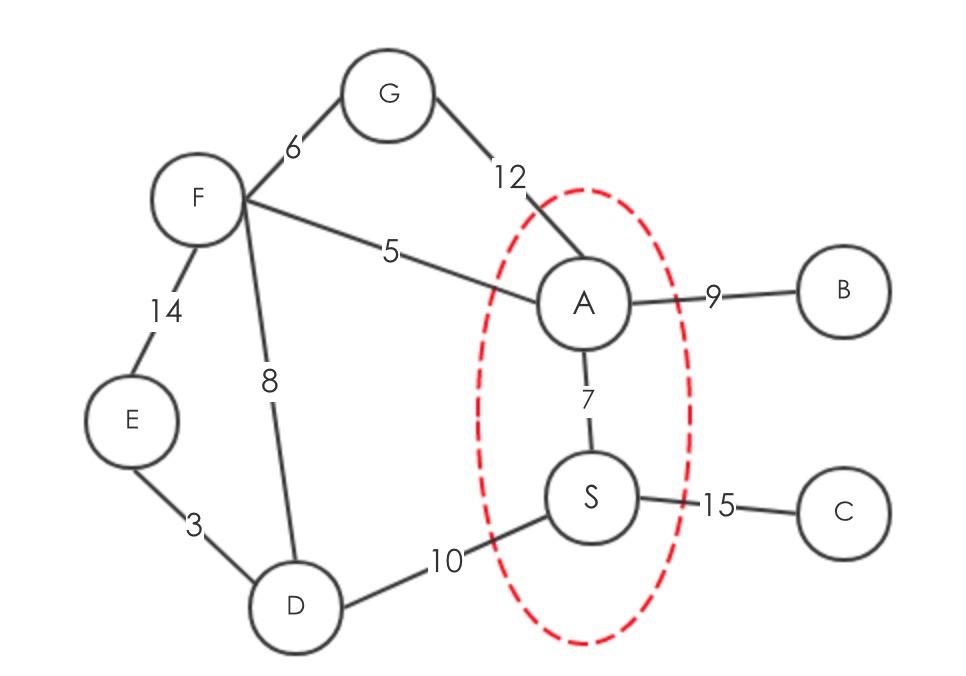
初始的图如下
选取节点s in S，其它的为V-S 按照初始化的规则得到
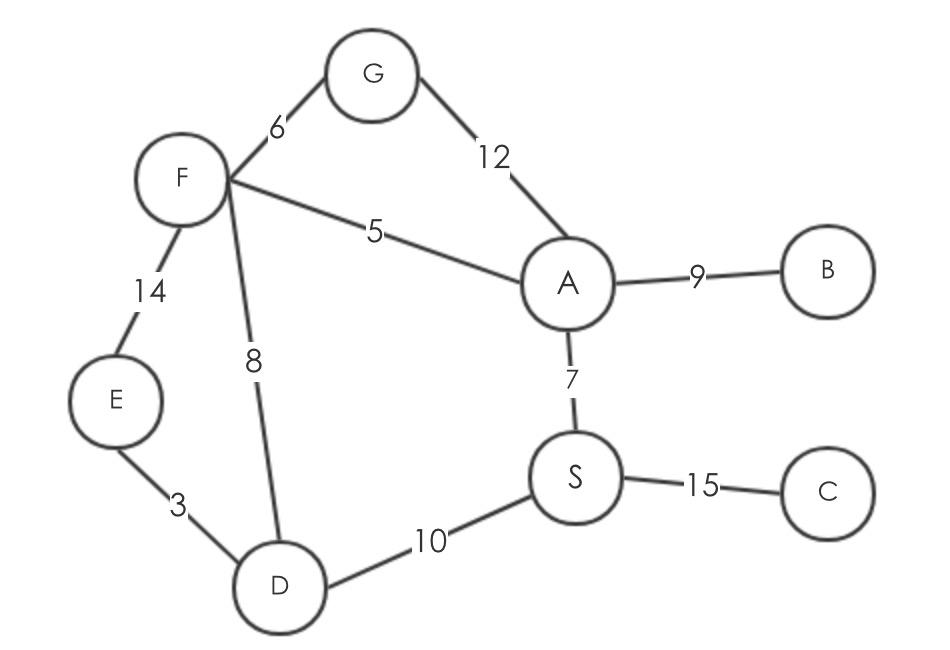
然后获取最小key的节点，显然他就是S
获取S的所有邻接表，比较crossing cut的边的权值和当前Q中存储的key的大小，保留小的，得到
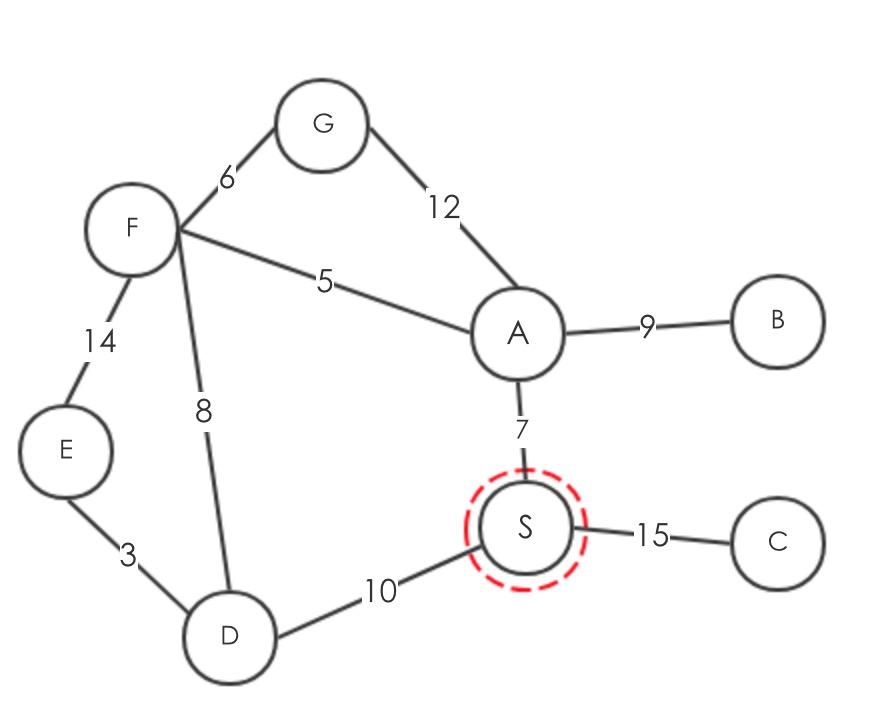
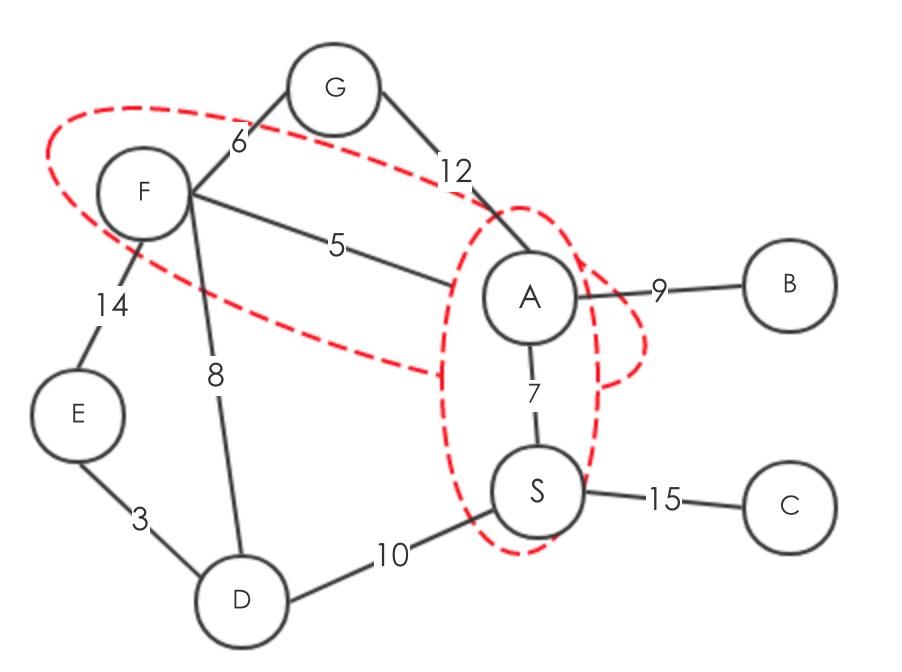
再找到Q中最小的为A，将两者记下来
再查看所有S的邻接表，更新Q的权值，得到
获取最小值为5,将它放入S中
再次更新Q得到
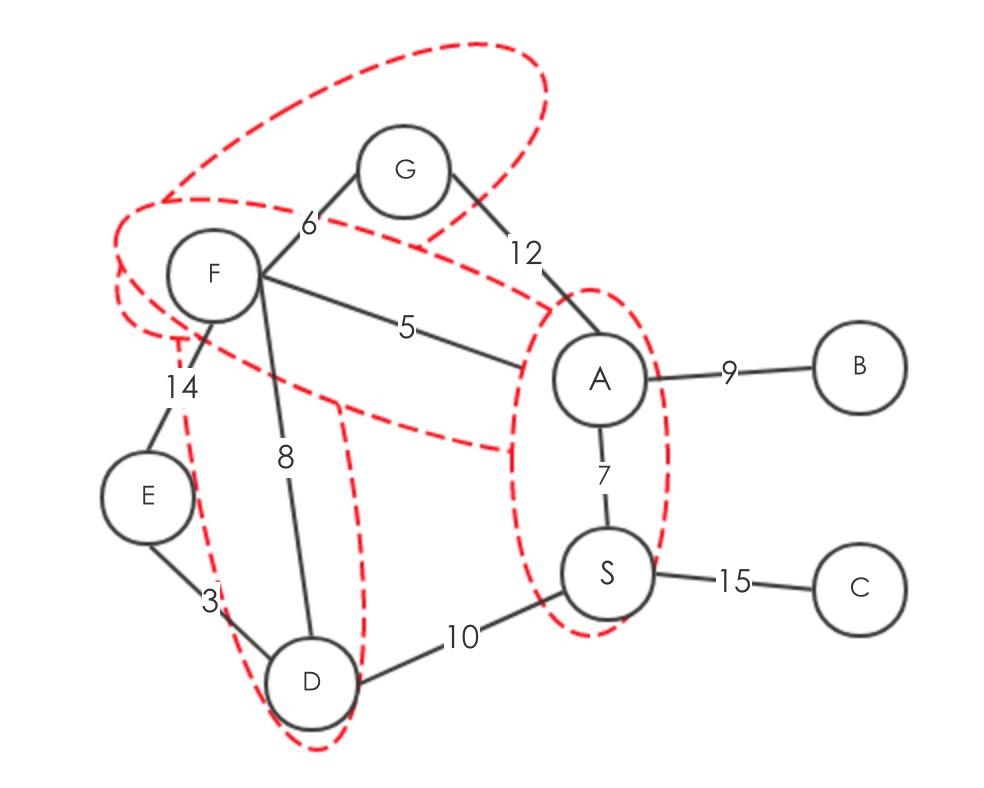
获取最小是为6，得到
再更新Q
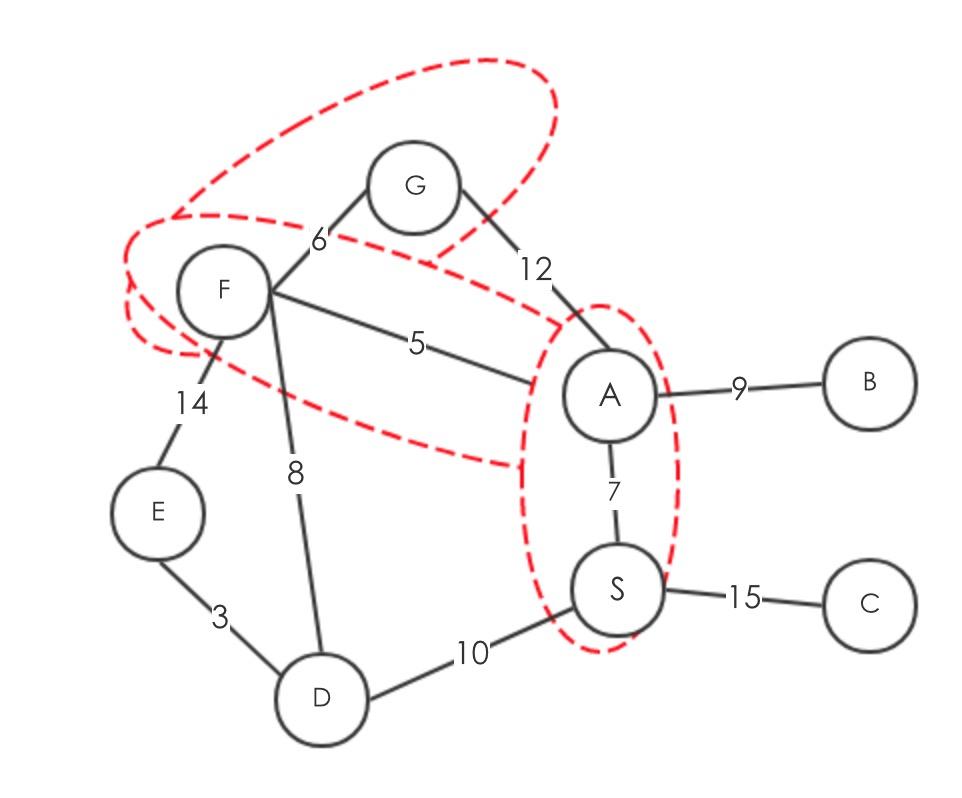
最小值为8
更新Q得到
最小值为3
更新Q得到
最小值为9
更新Q得到
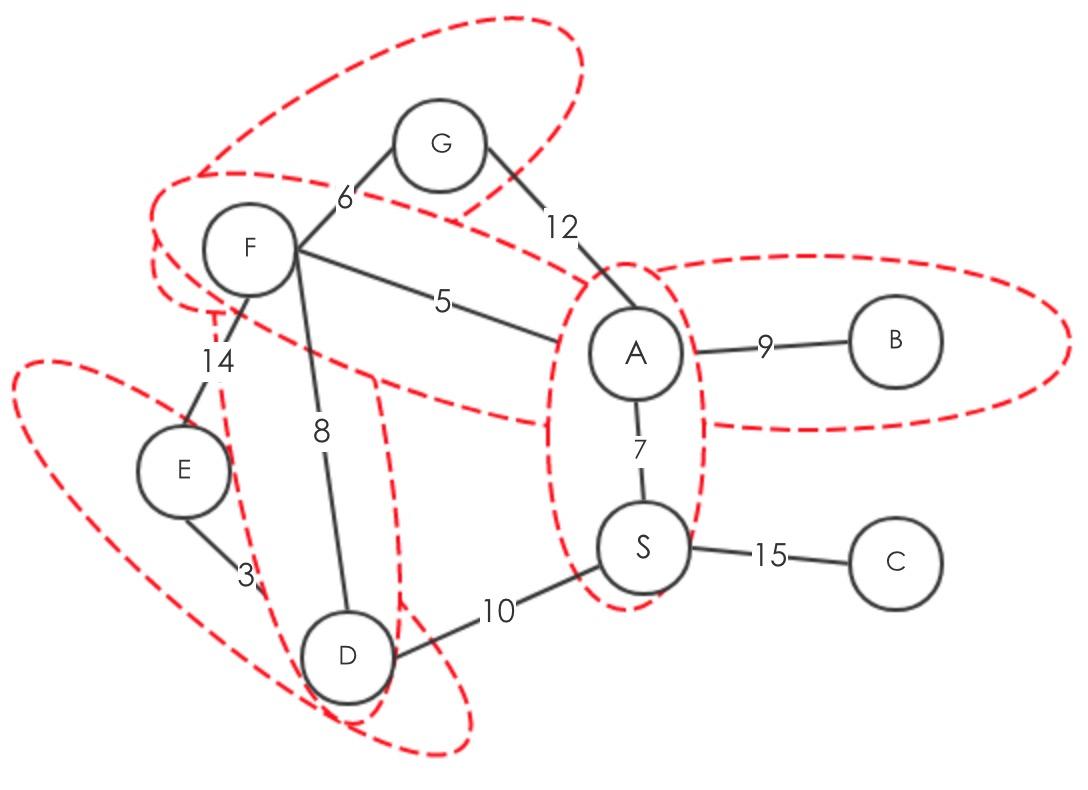
最小值为15
最终得到MST为
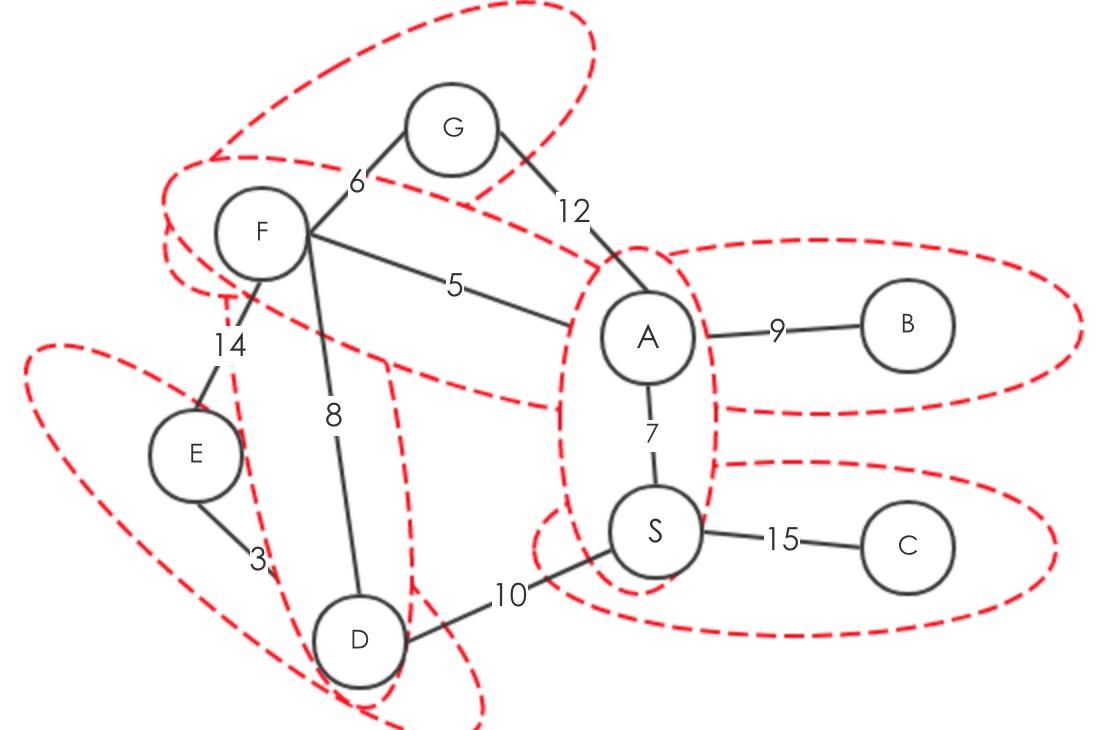
运行时间
在整个过程中，涉及V次的从优先级队列中获取最小值，以及边两倍次的减少key的值，所以总的时间为
使用斐波那契堆可以达到VlgV+E
Kruskal’s算法
核心思想：全局最小的corssing cut边必定属于最小生成树，这个过程不能生成环，需要追踪两个节点是否已经互相连接了
追踪的数据结构是 Union-Find 结构，包含3个功能，Make-Set:创建一个集合；Find-Set:找到当前元素在那个集合；Union:合并集合
- 刚开始的时候T什么都没有
- 对每个节点v都执行一遍Make-Set
- 为了找到全局最小的crossing cut，对整个的边通过权值按照递增来排序
- 按照增序遍历所有的边，如果两个节点u和v属于不同的集合(crossing cut)，那么可以合并边T=TU{e},然后将这两个集合合并Union(u,v)
时间分析
在使用Union-Find数据结构的基础上能够做到时间为O(ElgE+Eα(V))，假设权重为正整数而且最大值是个常量，那么排序可以达到常量的时间，这个时候，算法所需要的时间就是O(E),整体不Prims算法要好
最快的MST 算法运行期望时间是O(V+E),Karger, Klein, and Tarjan 1993发明