动态规划应该用于最优化问题
最优化问题指的是,解决一个问题可能有多种可行的值来解决问题,但是我们需要一个最优的(最大或者最小)值
动态规划适用于子问题不是独立的情况,即各个子问题之间包含公共的子问题。动态规划对每个子问题只计算一次,保存其计算结果到”一张表”,重复利用,从而优化执行。
分治法则是把一个大的问题划分成一些独立的子问题,递归求解子问题的情况;贪心算法则是会先选择当时看起来是最优的选择,然后再求解一个结果的子问题
如何使用动态规划
以斐波那契数列为例。一般的求解方式为递归,运行时间为 

fib(n):
if n<=2:f=1;
else: f= fib(n-1)+fib(n-2);
return f;
可以简要分析下这个执行过程:要去求解 fib(n),首先要知道fib(n-1)和fib(n-2),要计算fib(n-1)则需要知道fib(n-2)和fib(n-3),要计算fib(n-2)则需要知道fib(n-3)和fib(n-4),依此类推。
很明显可以看到:如果计算出了fib(n-1)的子问题和fib(n-2)的子问题存在依赖性,要计算fib(n-1)必然要计算fib(n-2);同时如果复用了fib(n-2)那么当计算fib(n-1)就非常简单,直接相加即可。这也就是复用子问题处理结果。
fib(n):
memo={}
if n in memo:return memo[n];
if n<=2:f=1;
else f=fib(n-1)+fib(n-2);
memo[n]=f;
return f;
分析可知:memo的存在使得实际产生调用的只有 fib(1) …. fib(n),共n次,其余的直接从memo中获取,使用常量的时间。可得运行时间为
int fib(int n){
if(n<=2){
return 1;
}
int f1=1,f2=1;
for(int i=3;i<=n;i++){
int f=f1+f2;
f1=f2;
f2=f;
}
return f2;
}
它的运行时间为
这种计算方式,它实际上是相当于进行了拓扑排序,即我只有先执行完fib(n-2),再执行fib(n-1),然后才执行fib(n)
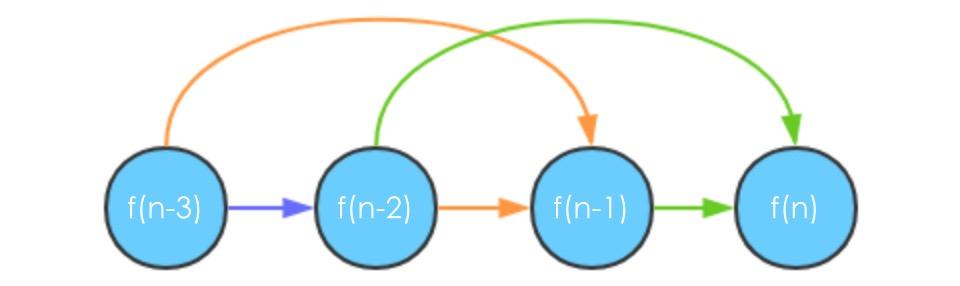
1、 斐波那契数列求值是可以分解成多个子问题 fib(k),且一共有n个
2、 子问题之间存在依赖关系:
3、 每个子问题的处理是按照拓扑排序的顺序进行,它的顺序为 k=1,…,n
最终去解决了原来的问题
子问题个数 * 每个子问题的处理时间=O(n)
拓扑排序
斐波那契数列中的拓扑排序,它本质上类似拓扑排序的DAG最短路径
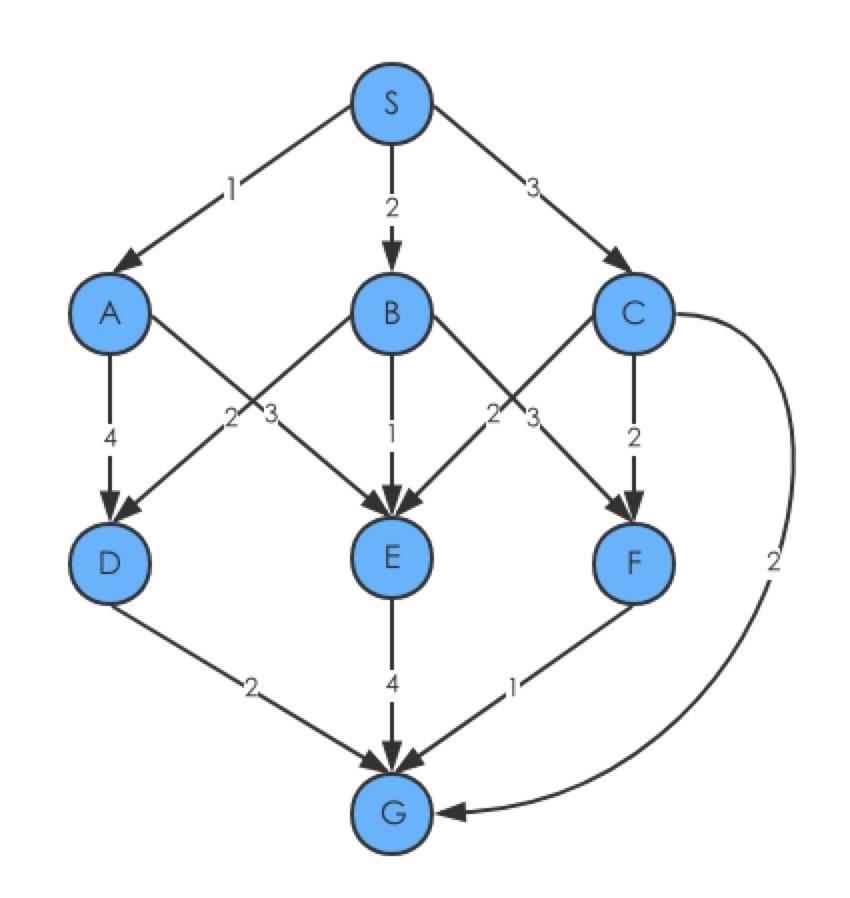
每条边都访问了一遍,然后初始化了每个顶点的值,它的运行时间为O(V+E)
计算过程可以看到:
1、 最短路径会被划分成多个子问题,比如



2、 子问题之间是存在依赖关系,比如



3、 整个处理的过程按照 SABCDEFG的拓扑顺序进行处理
一般的图拓扑排序为
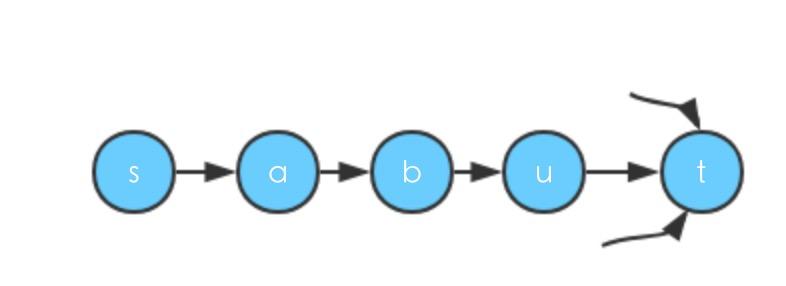

就是需要递归调用处理的部分
对于DAG:
indegree(t):入度数也就是类似(u,t)边的数量,需要去遍历所有t的入边
O(1):判断是不是有入边
总共的执行时间为
当图中有环的时候求最短路径产生的问题
要求s到v的最短路径
,首选需要去求
,然后是
,到b节点有两条路径:
和
,此时去memo中查
是不存在的,又会这回查询,导致了一个死循环
解决图中有环的时候求最短路径的问题
方式是去环,将原来的图一层一层的展开。
假设从s到v需要的路径为k步,那么可以得到=
,当k递减到0的时候,其实也就是从s到s本身
所需要的展开层数为:|V|-1 对于求最短路径来讲,最长不能超过|V|-1,否则就是成环,会造成循环的情况(从0开始的计数),这就是为什么Bellman-Ford的外层循环是 |V|-1
每层的节点数为所有的节点。那么总共的节点数为|V’|=|V|(|V|-1)+1=O(
),边数是|E’|=|E|(|V|-2)+1=O(VE)。转换后的图是DAG图,那么实际上的时间为O(V’+E’)=O(VE)。这也就是
从动态规划的角度去看Bellman-Ford算法节点的数目是1个源点,边的数目是每多一层实际上就多了加了一遍所有的边。
从斐波那契和最短路径的例子看出,要使用最短路径,需要确保子问题之间是互相依赖的,这样能够重复利用子问题产生的结果,而要去重复利用子问题,那首要条件是找到子问题是什么?然后在多个子问题之间选择最优的结果,并按照拓扑排序的顺序进行计算
使用动态规划的一般步骤是什么?
1、 定义子问题 :一般来讲子可以从输入条件来寻找,如果输入条件少了一项,我解决这个问题的方式会发生改变吗?如果不会,那么它基本就是子问题
计算子问题的数量
1、 思考:明确要去尝试所有可能方式,选取最好的一个。选取中要思考
- 获取到的输入项是否应该被选入子问题的结果之中?
- 有什么途径能够使子问题扩展到原有的问题?
- 子问题要计算原有的问题,增加了什么变化的因素?
计算选择的数量
1、 关联所有的子问题:根据思考得到父子问题的关联关系
计算单个子问题所需要处理的时间
1、 重用子问题结果并记下新的结果
计算总耗时
最终解决原有的问题,它消耗的时间为: 子问题的数量 * 每个子问题处理所需要时间
总的来说就是:尝试所有可能的子问题的结果,将最好的可能子结果存储下来,然后重复利用已经解决的子问题,递归去解决所有的问题(思考+记忆+递归)
一定要用动态规划吗?
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。比如
输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
乍看之下,要求连续最大和,首先得计算出子串的最大和,才能去计算原始数组的最大和,也就是说
1、 子问题是:子数组的最大和
2、 依赖关系:dp(i)=max(i,i+dp(i-1)),增加了一个新的元素扩展子问题,得到原问题,然后从扩展的结果和原有的结果中取获取一个最优解
3、 dp(i-1)是可以重用的
public int maxSubArray(int[] nums) {
int max=Integer.MIN_VALUE;
Map<Integer,Integer> mem=new HashMap<>();
for(int i=0;i<nums.length;i++){
//按照一定顺序执行
int v=dp(i,nums,mem);
if(v>max){
max=v;
}
}
return max;
}
public int dp(int i,int[] nums,Map<Integer,Integer> mem){
Integer v=mem.get(i);
if(v!=null){
//重用子问题的结果
return v;
}
int sum = nums[i];
if(i==nums.length-1){
mem.put(i,sum);
return sum;
}
//先计算子问题
int cSum = dp(i+1,nums,mem);
int tempV = sum+cSum;
//明确父子问题之间的关系,存储新的子问题结果
if(tempV<sum){
mem.put(i,sum);
return sum;
}
mem.put(i,tempV);
return tempV;
}
分析可以看到,它的执行为需要遍历一遍整个的数组,然后要去计算的子问题包括 n-1,n-2,..,1,耗时为 O(n+n-1)=O(2n)=O(n),同时需要一个O(n)的空间存储。
public int maxSubArray(int[] nums) {
int max=nums[0];
int currMax=nums[0];
for(int i=1;i<nums.length;i++){
int temp=nums[i]+currMax;
if(temp>nums[i]){
currMax=temp;
}else{
currMax=nums[i];
}
if(max<currMax){
max=currMax;
}
}
return max;
}
通过这种方式,使用的空间为O(1),时间就是O(n)。
由此可见动态规划本身只是一种解决问题的思想,并不是说动态规划得到的最优解就是解决问题的最佳方案








 就是需要递归调用处理的部分
就是需要递归调用处理的部分

 ,首选需要去求
,首选需要去求  ,然后是
,然后是 ,到b节点有两条路径:
,到b节点有两条路径: 和
和 ,此时去memo中查
,此时去memo中查 是不存在的,又会这回查询,导致了一个死循环
是不存在的,又会这回查询,导致了一个死循环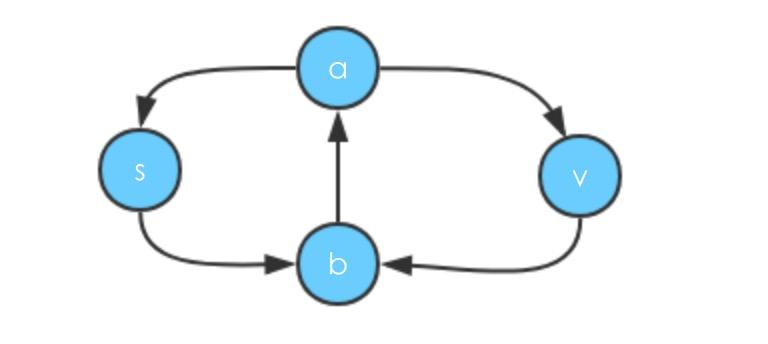
 =
= ,当k递减到0的时候,其实也就是从s到s本身
,当k递减到0的时候,其实也就是从s到s本身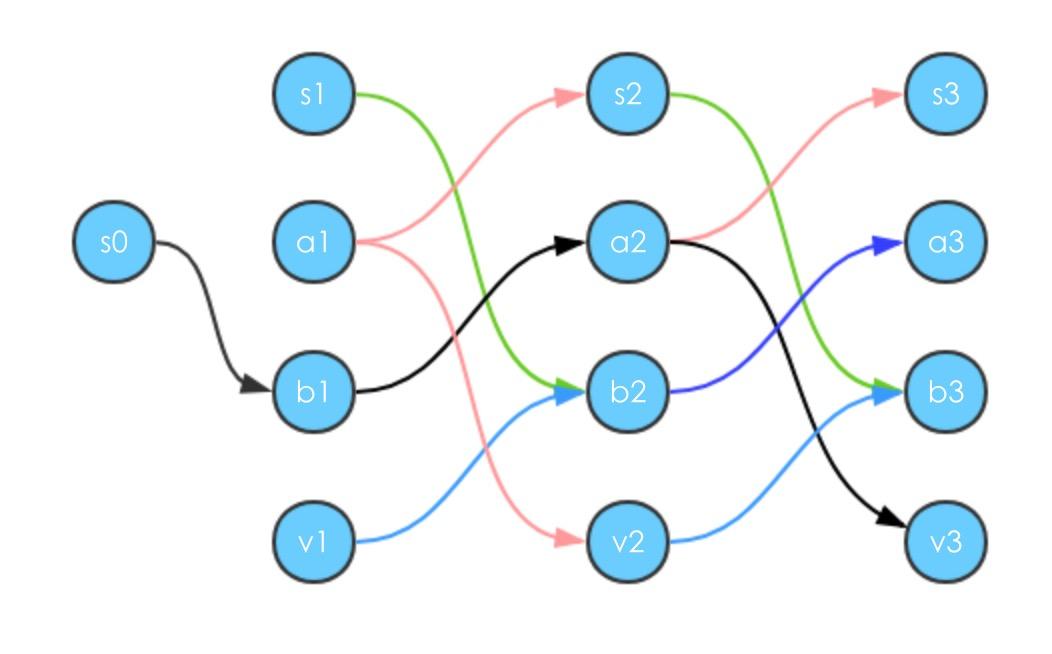 所需要的展开层数为:|V|-1 对于求最短路径来讲,最长不能超过|V|-1,否则就是成环,会造成循环的情况(从0开始的计数),这就是为什么Bellman-Ford的外层循环是 |V|-1
所需要的展开层数为:|V|-1 对于求最短路径来讲,最长不能超过|V|-1,否则就是成环,会造成循环的情况(从0开始的计数),这就是为什么Bellman-Ford的外层循环是 |V|-1 ),边数是|E’|=|E|(|V|-2)+1=O(VE)。转换后的图是DAG图,那么实际上的时间为O(V’+E’)=O(VE)。这也就是
),边数是|E’|=|E|(|V|-2)+1=O(VE)。转换后的图是DAG图,那么实际上的时间为O(V’+E’)=O(VE)。这也就是