算法导论(MIT 6.006 第13讲)
什么是图搜索？
搜索可以理解为探索，给定一个图上的点S和A，需要找到从S到A的一个路径
图的基础概念
一个图用 G=(V,E) 表示,V是顶点的集合，E是边的集合。如下所示有两种图
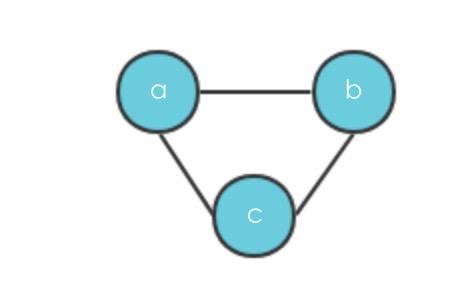
1、 无向图，V={a,b,c},E={{a,b},{b,c},{a,c}}
2. 有向图，V={a,b,c},E={(a,b),(b,a),(c,a),(b,c)}
实际应用有哪些？
网络爬虫、社交网络、网络包传播、垃圾回收算法等
如何用算法表示图？
使用邻接表。它是一个数组(Adj表示)大小是 |V|，每个元素是指向一个链表的指针，遍历的方法如下
for each vertex u in V
Adj[u] stores u's neighbors
比如，上所述的有向图来说 Adj[a]={b},Adj[b]={a,c},对无向图来讲 Adj[a]={(a,c),(a,b)}
这种表现形式所需要的空间大小为
(V+E)，|V|个顶点和|E|条边
(V+E)，|V|个顶点和|E|条边
广度优先算法是如何搜索一张图的？
目标：对于一个给定的节点S 
V,通过它来遍历它所能到达的所有节点
时间要求：O(V+E)
思路：查看给定节点，通过0步移动，能够到达的节点，这个节点就是s本身，然后从s移动一步，也就是s的邻接表，找到他能到达的节点，依次类推,需要避免重复
BFS(s,Adj):
level={s:0} //第0步能到达的节点
parent={s:None}
i=1 //第0步就是s,已经到达，从第一步开始
frontier=[s] //前一层已经经过的节点 level=i-1
while frontier: //在已经经过的节点找它的相邻节点
next=[] //当前层找到的节点
for u in frontier:
for v in Adj[u]:
if v not in level: //当前节点没有在其它层出现过，从而避免重复
level[v]=i
parent[v]=u
next.append(v)
frontier=next
i+=1 //走下一层
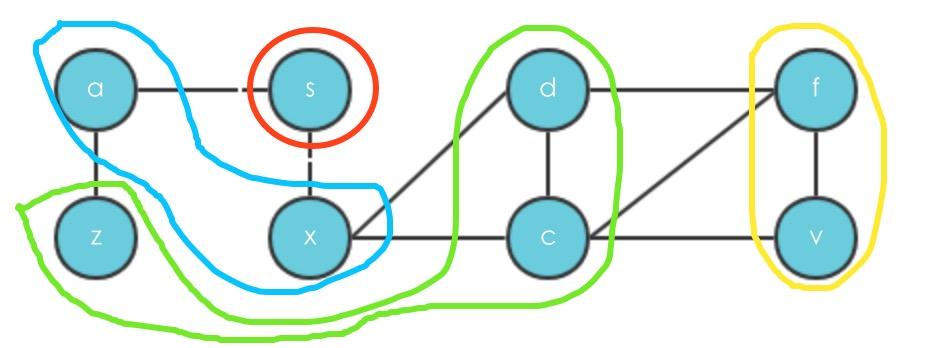
以无向图为例
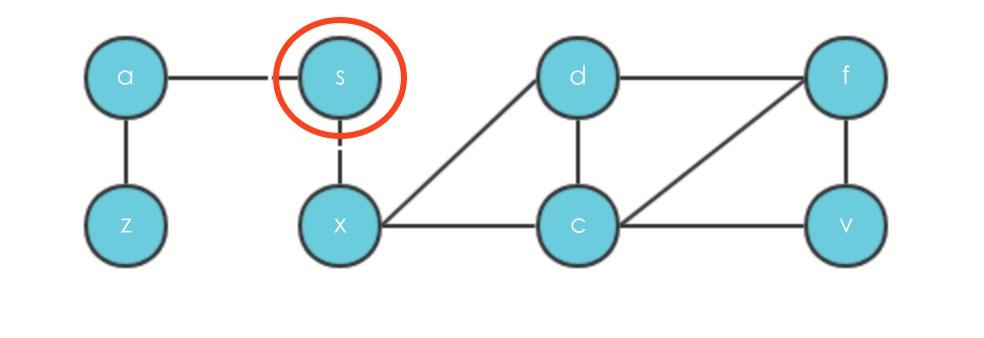
1、 初始状态，处于第0层，i=0,s没有父节点,已经经过的节点只有s
2. 从s移动0步，s的相邻节点是a和x,他们没有在之前的level存在，所以需要添加到level中。执行完后
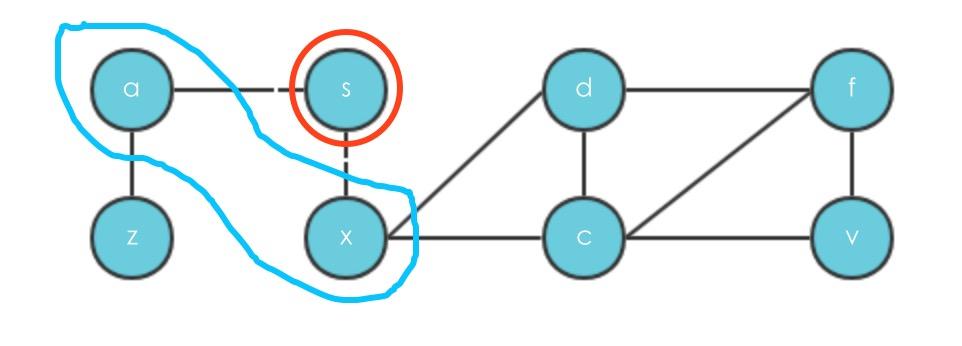
level={s:0,a:1,x:1}
parent={s:None,a:s,x:s}
frontier={a,s}
i=2
3. 以新的frontier为基础，再往前一步，发现a有z和s，但是s已经经历过了，不再添加，依次类推x。执行完之后
level={s:0,a:1,x:1,z:2,x:2}
parent={s:None,a:s,x:s,z:a,d:x,c:x}
frontier={z,d,c}
i=3
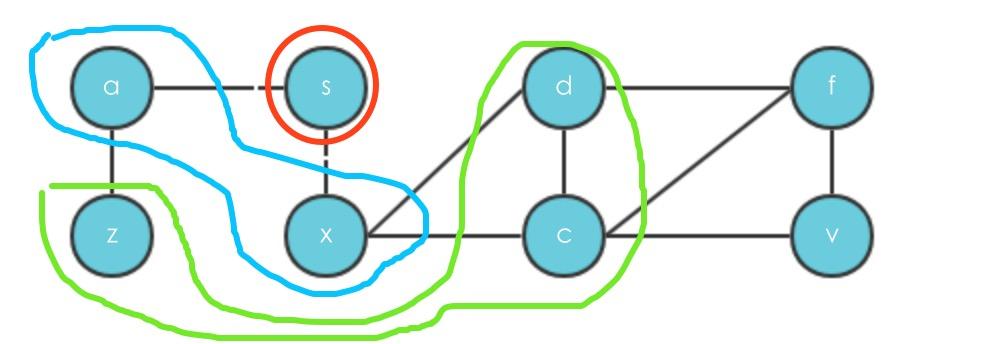
1、 以新的frontier为基础，再往前一步，发现z的唯一邻接节点只有a，但是a已经在level 1中，不再添加。执行完之后
level={s:0,a:1,x:1,z:2,x:2,f:3,v:3}
parent={s:None,a:s,x:s,z:a,d:x,c:x,f:d,v:c} frontier优先存的是d
frontier={f,v}
i=4
5. 以新的frontier为基础，再往前一步，发现f,v的邻接节点都已经计算过，不再计入，因此最后
frointer={}
i=5
至此结束
耗时分析
BFS所做的策略是先找到每一层的节点，再去找它的邻接表，耗时可以从两部分来看，1个是必须遍历所有节点，为V，另外每一层遍历的边的数量为 
v
V
，即每个顶点的边的个数，对于有向图来讲是E，无向图就是2E，这样总的时间就是 
(V+E)
优点
1、 当想知道某个节点到原点s的最短路径时，可以直接从level上获取，并且parent提供的指针就是这条路径
2、 能直接感知到从s能否到达某个节点t