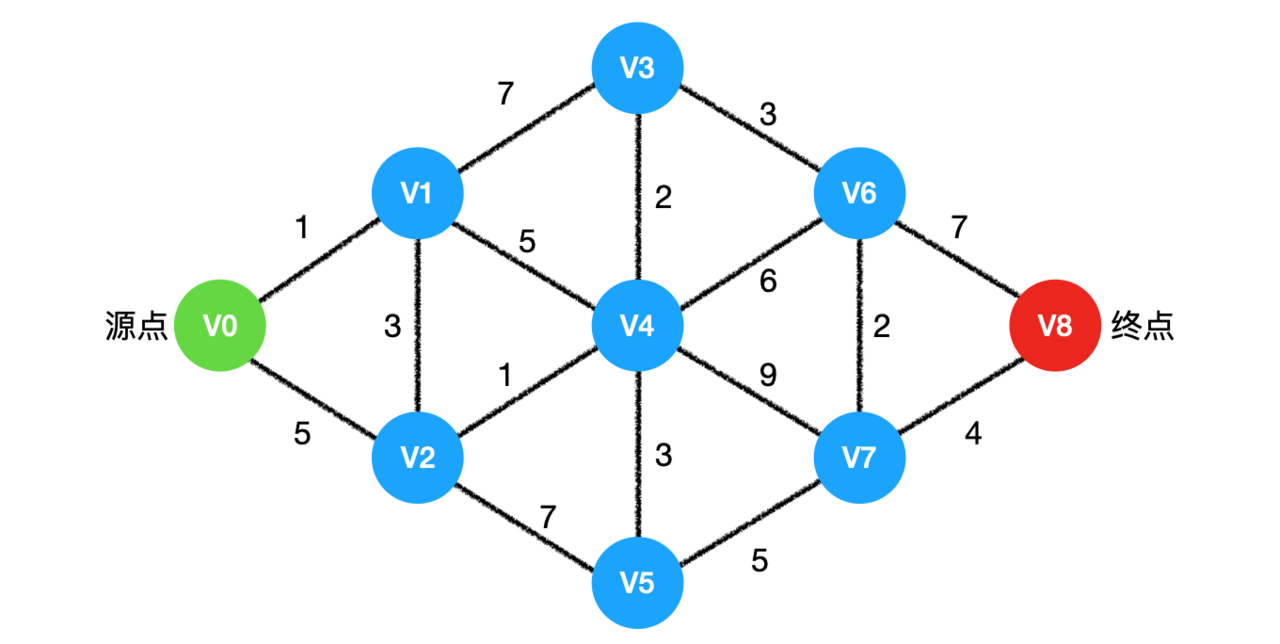
对于网(带权值的图)来说,最短路径是指两点之间经过的的边的权值之和最少的路径,路径上第一个顶点是源点,最后一个是终点。
那么如何计算出源点到终点的最短路径?
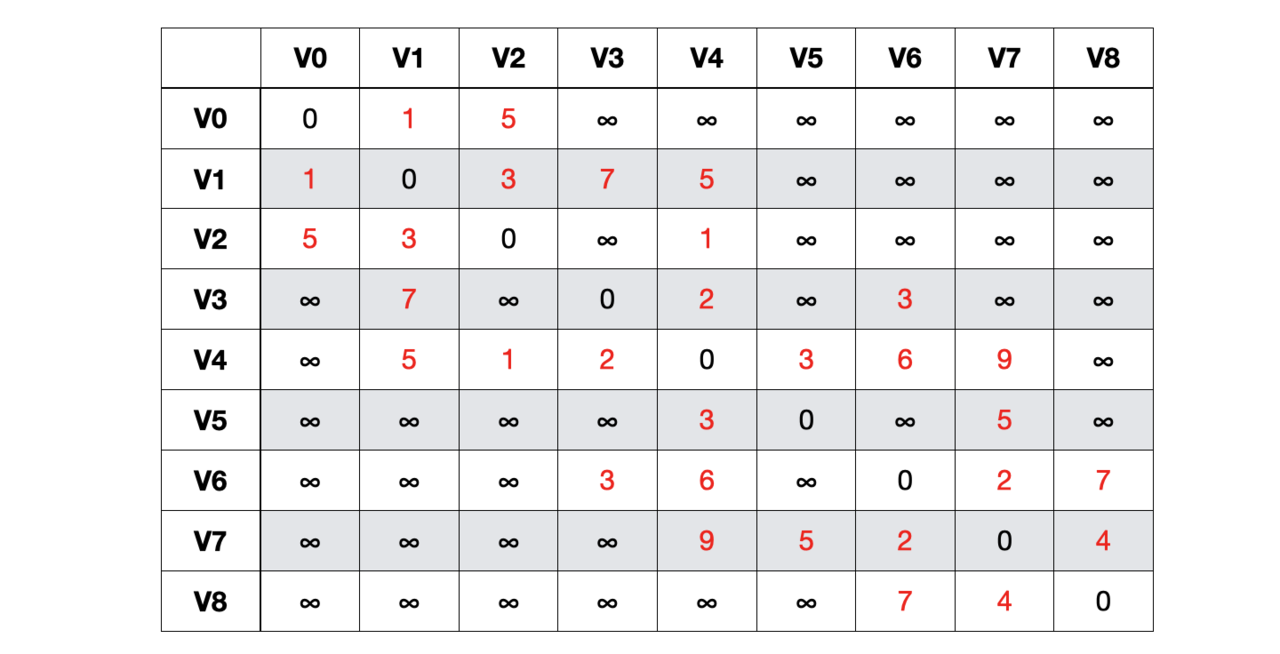
利用邻接矩阵。
Dijkstra算法(迪杰斯特拉)
Dijkstra算法是按照路径长度递增的次序产生最短路径的算法。
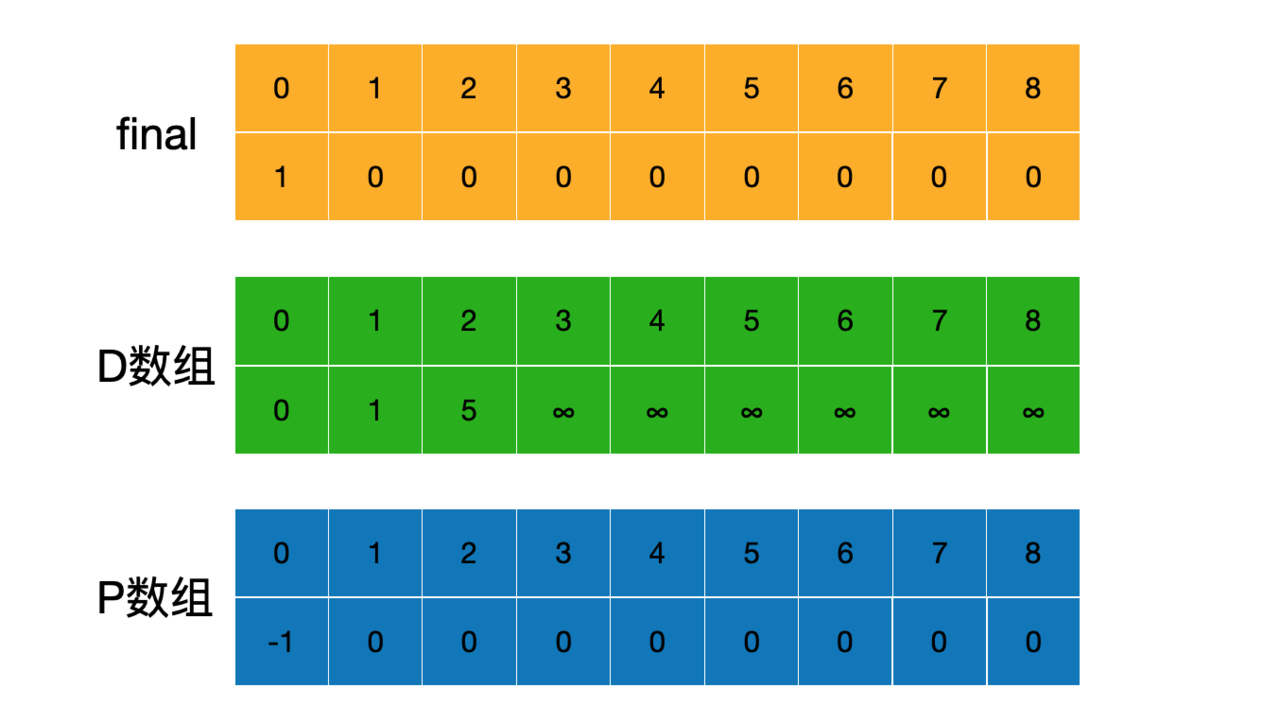
该算法需要用到三个数组,final,D,P,我们先了解下这三个数组用来做什么。
final数组:
用来记录顶点是否已经找到最短路径,即final数组中数据为1的下标对应的顶点表示已经在最短路径中,例如说源点肯定是在最短路径,那么final[0] = 1;
D数组:
用来记录V0顶点到其他顶点的路径,由上图可知,V0与V1,V2有直接联系,与其他顶点是间接联系,可以暂时初始化D数组为 [0,1,5,∞,∞,∞,∞,∞,∞]。∞(无穷)代表暂时未知,之后根据循环向后计算,会对D数组中的数据进行对比更新操作,以求的V0到其他顶点的最短路径的权值和。
例如D数组初始化后,V0到V2的距离是5,但其实我们可以计算出V0->V2要大于V0->V1->V2,这样进行对比后,就需要对D数组进行更新,[0,1,4,∞,∞,∞,∞,∞,∞]。依次向后求的其他位置的数据
P数组:
用来记录前驱顶点的下标。初始化时可以默认V0是其他顶点的前驱顶点,V0没有前驱顶点,所以初始化为[-1,0,0,0,0,0,0,0,0]。第一次循环后可知,V1的前驱顶点是V0,而V2,V3,V4的前驱顶点是V1,那么P数组更新后,[-1,0,1,1,1,0,0,0,0]。
核心代码
/*
Dijkstra 算法
G: 网图;
v0: V0开始的顶点;
P[v]: 前驱顶点下标;
D[v]: 表示从V0到V的最短路径长度和;
*/
void ShortestPath_Dijkstra(MGraph G, int v0, Patharc *P, ShortPathTable *D)
{
int v,w,k,min;
k = 0;
// final数组 记录0-n顶点,是否已经找到最短路径,同时也作为标签来表示顶点是否已加入最短路径
int final[MAXVEX];
// 初始化数据
for (v = 0; v < G.numVertexes; v++) {
// 所有顶点初始化为未知的最短路径 初始化0
final[v] = 0;
// 与V0顶点有连接关系的顶点 最短路径的权值
(*D)[v] = G.arc[v0][v];
// 初始化所有的前驱顶点为0
(*P)[v] = 0;
}
// V0 默认加入在最短路径上
final[0] = 1;
// V0 到 V0的路径权值是0
(*D)[0] = 0;
// V0顶点没有前驱顶点,给他-1
(*P)[0] = -1;
// 循环 求的V0到其他顶点的最短路径
for (v = 1; v<G.numVertexes; v++) {
min = INFINITYC;
for (w = 0; w<G.numVertexes; w++) {
// final[w] != 1 即未加入到最短路径的顶点
// (*D)[w] < min 找到D数组中最小的路径权值
if (!final[w] && (*D)[w] < min) {
// 循环结束时,k:距离最短的顶点,min:最短的路径权值
k = w;
min = (*D)[w];
}
}
// 将k顶点标记为1 即已加入最短路径
final[k] = 1;
// 循环找到k顶点可能走向的顶点,并更新D P 数组
for (w = 0; w < G.numVertexes; w++) {
// final[w] != 1 未加入到最短路径的顶点
// G.arc[k][w] + min 是否小于D数组中对应w位置的值 小于则更新D和P
if (!final[w] && ((G.arc[k][w] + min) < (*D)[w])) {
// w顶点的权值更新为更小的 G.arc[k][w] + min
(*D)[w] = G.arc[k][w] + min;
// w顶点的前驱顶点是k
(*P)[w] = k;
}
}
}
}
模拟一下循环过程
初始化
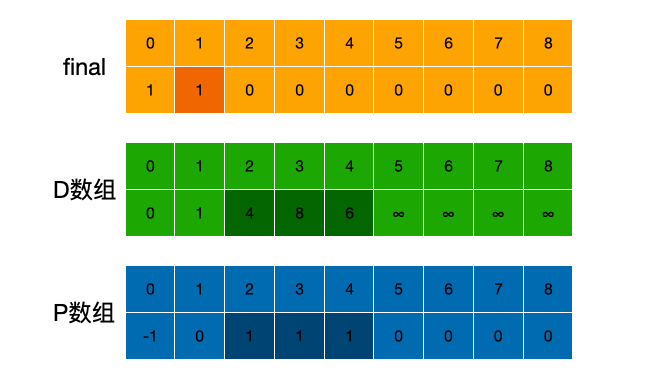
第一次循环后,
D数组中:遍历D数组,可知V0距离最短的距离应该是V0到V1,权值为1。k就等于1,min就等于1。循环找到k顶点V1,有直接联系的顶点V2,V3,V4,更新V0距离V2是V0->V1->V2为4,V0距离V3是V0->V1->V3为8,V0距离V4为V0->V1->V4为6。
P数组中:V2,V3,V4的前驱顶点为V1,对应位置更新为1
final数组中:V1加入了最短路径,对应位置更新为1,即已加入最短路径
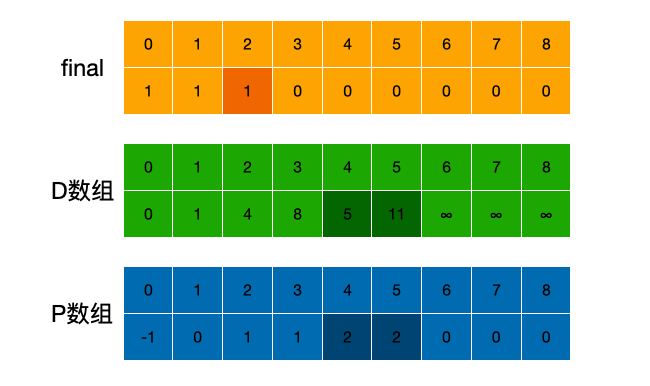
第二次循环:
D数组中:遍历D最短的权值对应的是V2,则k=2,min=4,更新V2有直接关系的顶点V4,V5,路径分别为1,7。这里我们可以看到,D数组中4下标对应的是6,即第一次循环中我们知道,V0到V4的最短距离为V0->V1->V4是6。但是现在我们可知,V0->V1->V2->V4距离为5,那么D数组4位置的数据要进行更新,同时也要更新下标5的数据,之前V0没有到V5的路径,现在可知V0->V1->V2->V5距离为11。
P数组中:4的前驱顶点由1改成了2,5的前驱顶点由0改成2
final数组:V2加入了最短路径,2的位置为1。
依次这样,直到V0与所有的顶点的距离都进行了比较。通过最终的D数组和P数组,我们可以知道源点V0到终点V8的权值和以及它的最短路径。
printf("最短路径路线:\n");
for(i=1;i<G.numVertexes;++i)
{
printf("v%d -> v%d : ",v0,i);
j=i;
while(P[j]!=-1)
{
printf("%d ",P[j]);
j=P[j];
}
printf("\n");
}
printf("\n最短路径权值和\n");
for(i=1;i<G.numVertexes;++i)
printf("v%d -> v%d : %d \n",G.vexs[0],G.vexs[i],D[i]);
/**
最短路径路线:
v0 -> v1 : 0
v0 -> v2 : 1 0
v0 -> v3 : 4 2 1 0
v0 -> v4 : 2 1 0
v0 -> v5 : 4 2 1 0
v0 -> v6 : 3 4 2 1 0
v0 -> v7 : 6 3 4 2 1 0
v0 -> v8 : 7 6 3 4 2 1 0
最短路径权值和
v0 -> v1 : 1
v0 -> v2 : 4
v0 -> v3 : 7
v0 -> v4 : 5
v0 -> v5 : 8
v0 -> v6 : 10
v0 -> v7 : 12
v0 -> v8 : 16
*/