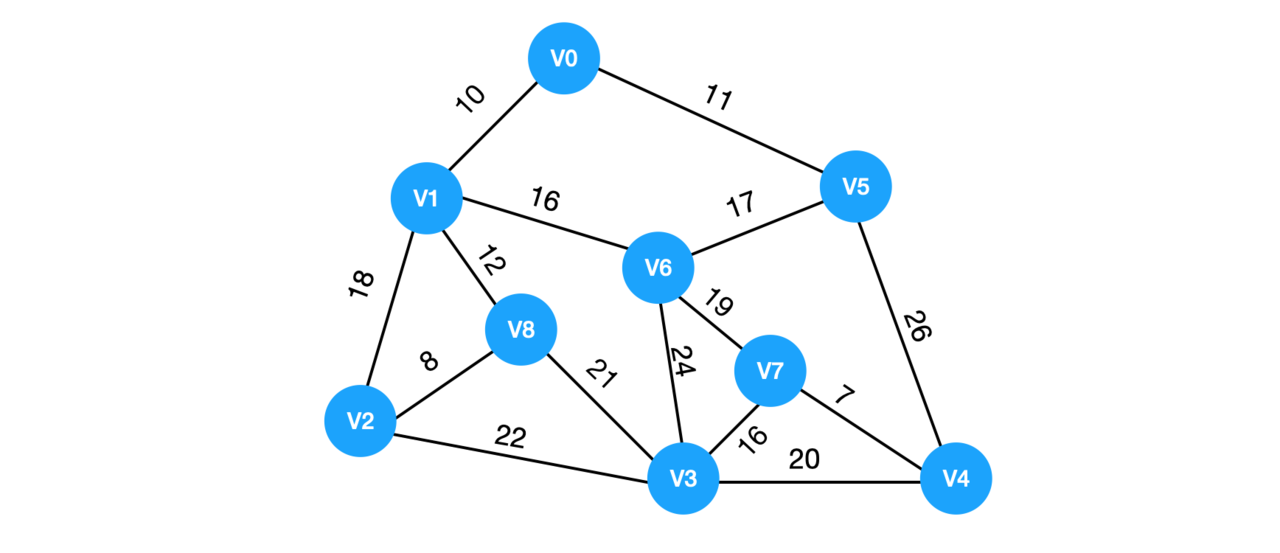
一个现实问题,为九个村庄架设通信网络,领导要求用最小的成本来实现,如何做呢?
显然这是一个带权值的图,即网结构。最小成本就是使用n-1条边将上图链接起来,并且使得权值的和是最小的,即架设的网线使用的最短。
最小生成树:把构成连通图的最小代价的生成树称为最小生成树
找连通图的最小生成树,有两种经典算法:普里姆算法(Prim),克鲁斯卡尔算法(Kruskal)。
普里姆算法
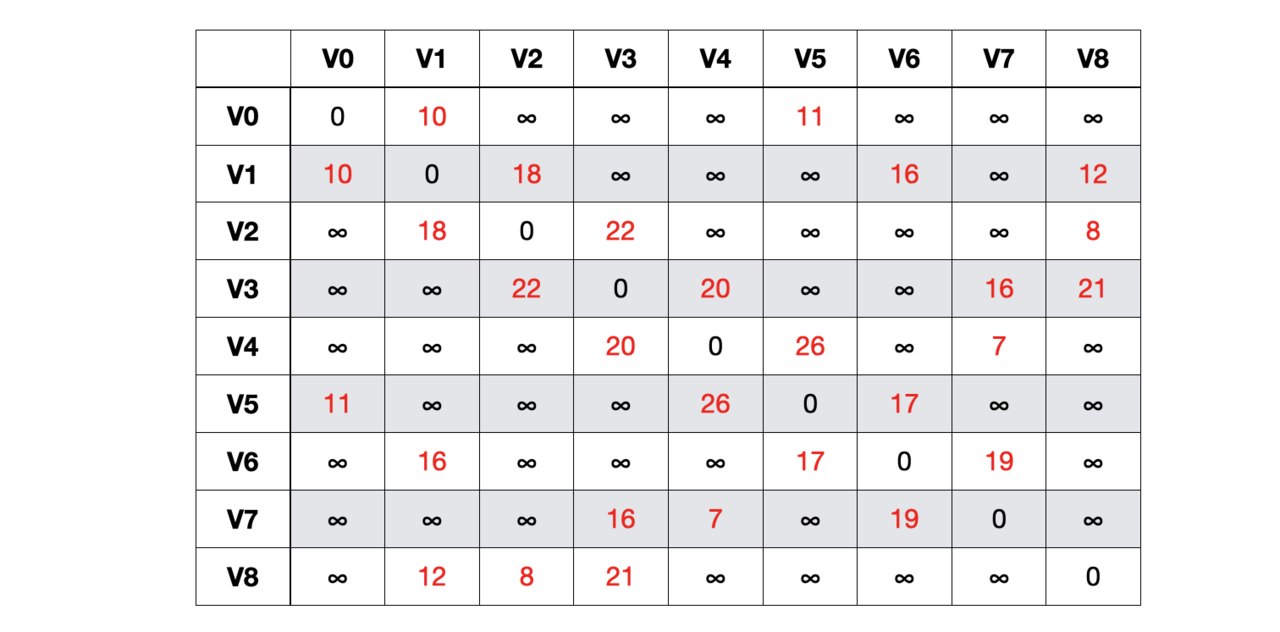
普里姆算法,需要先构造图的邻接矩阵。
// Prim算法生成最小生成树
void MiniSpanTree_Prim(MGraph G){
int min,i,j,k;
int sum = 0;
// 保存相关的顶点下标
int adjvex[MAXVEX];
// 保存相关顶点间边的权值
int lowcost[MAXVEX];
// 默认将V0顶点加入到最小生成树
lowcost[0] = 0;
// 初始化adjvex lowcost数组
for (i = 1; i<G.numVertexes; i++) {
// 将V0顶点相关的边权值存入数组
lowcost[i] = G.arc[0][i];
// 初始化 假设所有的顶点都与V0顶点有关联 之后会更新
adjvex[i] = 0;
}
for (i = 1; i<G.numVertexes; i++) {
// 初始化最小权值是∞ 遍历对比最小值就将min替换掉,始终保存最小的权值
min = INFINITYC;
j = 1;
k = 0;
// 循环所有的顶点,找到lowcost数组中权值最小的k
while (j<G.numVertexes) {
// 1.权值不为0 即还未添加到最小生成树
// 2.权值小于min
if (lowcost[j] != 0 && lowcost[j] < min) {
// 让当前权值替换为min
min = lowcost[j];
// 当前的下标存入k while结束时,k保存的是权值最小的下标
k = j;
}
j++;
}
/* 打印当前顶点边中权值最小的边 */
printf("(V%d, V%d)=%d\n", adjvex[k], k ,G.arc[adjvex[k]][k]);
// sum 保存权值和
sum+=G.arc[adjvex[k]][k];
// lowcost中k下标的值修改为0 表示k对应的顶点已加入最小生成树
lowcost[k] = 0;
// 循环所有的顶点,更新adjvex数组
for (j = 1; j<G.numVertexes; j++) {
if (lowcost[j] != 0 && G.arc[k][j] < lowcost[j]) {
// 更新lowcost数组中对应位置的权值 相当于添加
lowcost[j] = G.arc[k][j];
// 将下标为k的顶点存入adjvex
adjvex[j] = k;
}
}
}
printf("sum = %d\n",sum);
}