要了解哈夫曼编码,我们先要从哈夫曼树开始说起。哈夫曼树是美国数学家哈夫曼,在编码中用到的特殊的二叉树,也称为最优二叉树。
当时哈夫曼研究最优树的目的,是为了解决当时远距离通信的数据传输的最优化问题。比如说要传递的数据‘DLADKAIOELAKJL’,通过正常编码后的结果可能会非常的长,那么哈夫曼就研究出了这样的一种压缩编码方法。
1. 哈夫曼树
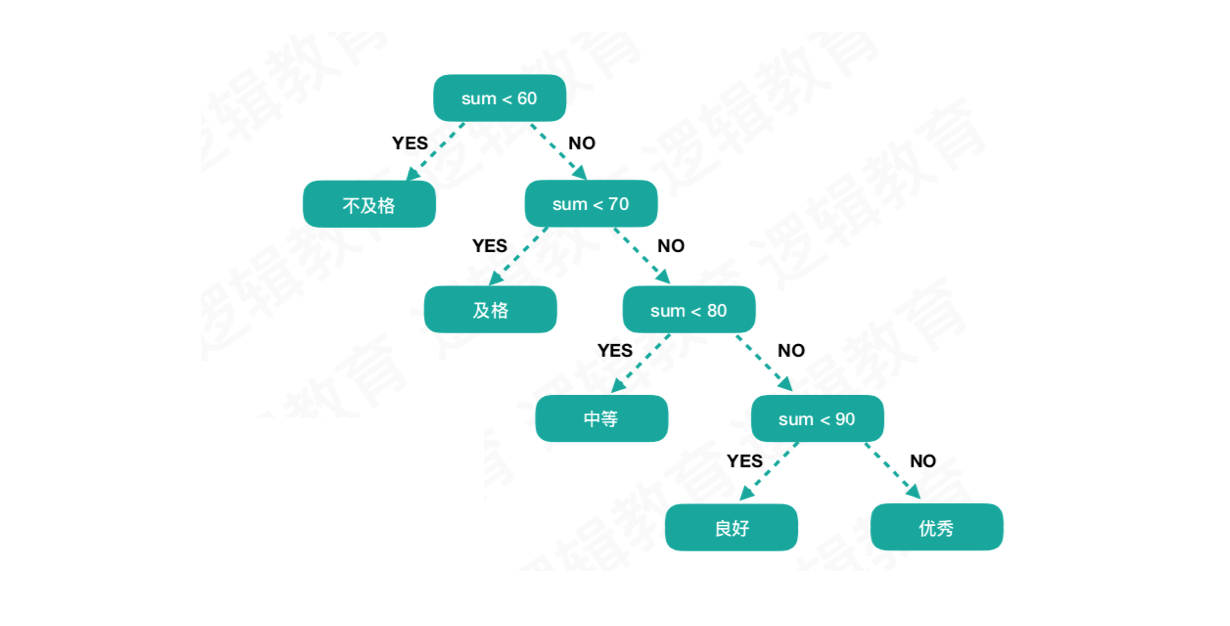
先从一个例子说起。学校考试成绩表:
if (num < 60) {
return "不及格";
}else if (num < 70){
return "及格";
}else if (num < 80){
return "中等";
}else if (num < 90){
return "良好";
}else{
return "优秀";
}
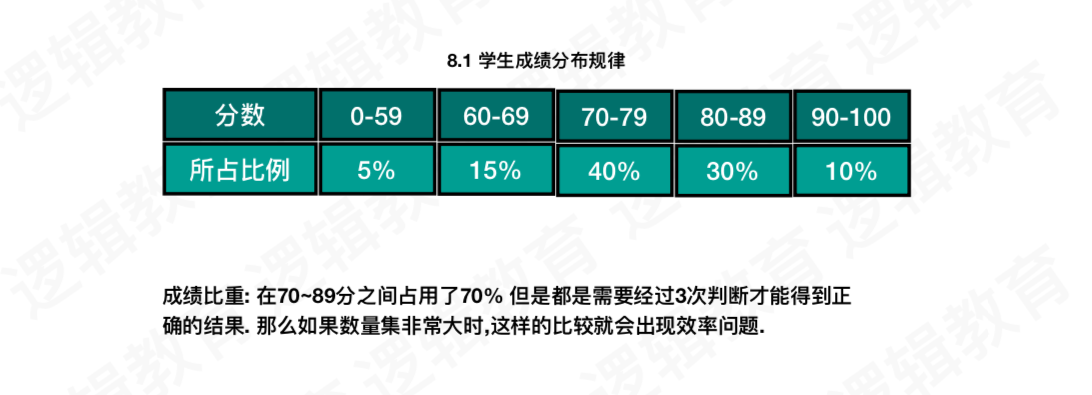
一般情况下,一张考卷的成绩大部分处于中等和良好的范围,优秀和不及格都是较少的,那么按照上边的程序,使得所有的成绩都需要先判断是否及格,再逐级向上判断,当数据当很大的时候,这样的算法是存在效率问题的。
数的路径长度:从树中的一个结点到另一个结点之间的分支构成两个结点之间的路径,路径上的分支数目称作路径长度。而树的路径长度就是从树根结点到每一结点的路径长度之和。
树的带权路径长度:树的带权路径长度WPL为树中所有叶子结点的带权路径长度之和,而结点的带权路径长度为该结点到树根结点之间的路径长度与结点上权的乘积。
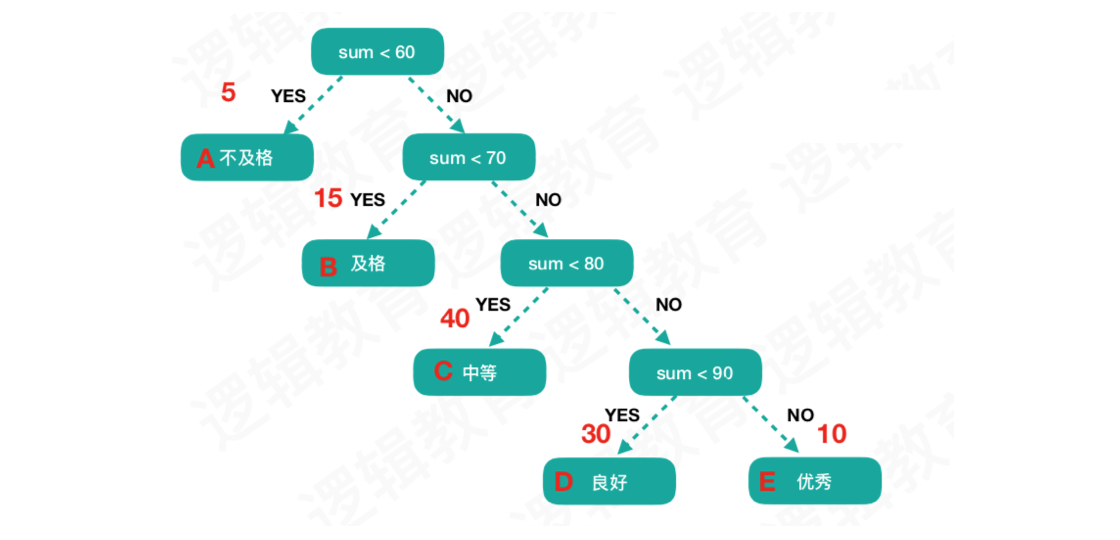
上面二叉树的路径长度就是:1+1+2+2+3+3+4+4 = 20.
上面二叉树的带权路径长度WPL就是:5*1 + 15*2 + 40*3 + 30*4 + 10*4 = 315.
那么我们如何进行一个优化呢?
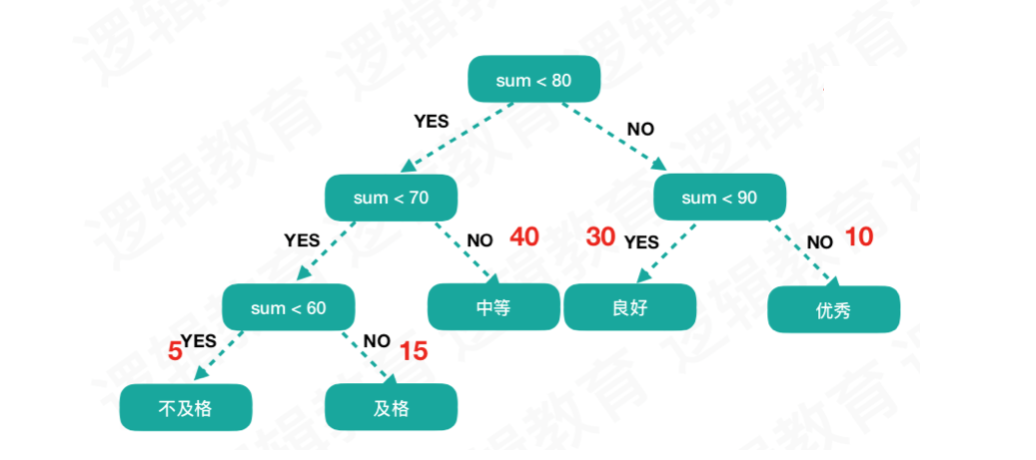
我们可以根据成绩分布所占比例(A:不及格,B:及格,C:中等,D:良好,E:优秀),来决定先对70-79范围进行判断,因为这个分数段的所占比例是最大的,从大到小依次进行判断。
那么它的带权路径长度就是:5*3 + 15*3 + 40*2 + 30*2 + 10 *2 = 220.
很明显下边设计的二叉树的带权路径长度要更短。
那么这样结果,就是最优二叉树了吗?
2. 哈夫曼树的构建
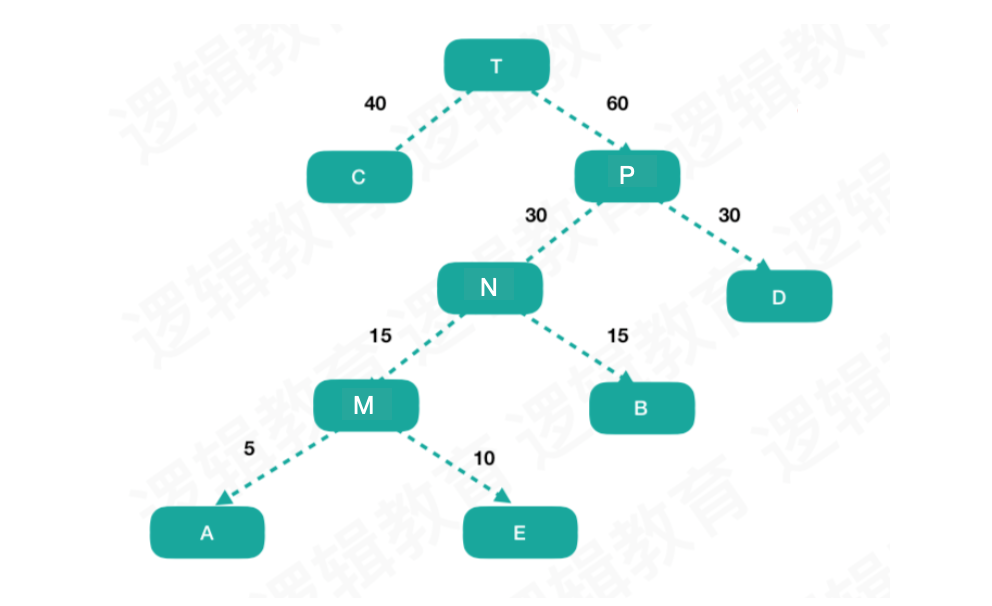
还是成绩的例子,我们来构建一个哈夫曼树:
1、 先把有权值的叶子结点按照从小到大的顺序排列称一个有序序列,即A5,E10,B15,D30,C40.
2、 取前两个最小权值的结点A5和E10,作为一个新结点M的两个子结点,相对较小的是左孩子,新结点M的权值就是两个叶子权值的和:5+10=15.
3、 用M结点将有序列表中的A5和E10替换下来,有序序列仍旧以从小到大的顺序排列,即M15,B15,D30,C40.
4、 重复第二步,将M15和B15作为一个新结点N的两个子结点,新结点N的权值就是15+15=30,
5、 重复第三步,用N结点将有序列表中的M15和B15替换下来,有序序列结果为,N30,D30,C40.
6、 如此一直重复第二步,第三步,直至组成一个二叉树,这就是哈夫曼树。
上图二叉树的带权路径长度WPL:40*1 + 30*2 + 15+3 + 10*4+5*4 = 205.
那么我们可以得出这样的结果,当我们使用这样的算法来输入成绩表的时候,效率是最优的。
3. 哈夫曼树的实现
实现代码
void haffman(int weight[], int n, HaffNode *haffTree){
int j,m1,m2,x1,x2;
// 1.哈夫曼树的初始化
// n个叶子结点的树中 一共有2n-1个结点
for (int i = 0; i<2*n-1; i++) {
// 前几个都是叶子结点,给叶子结点赋权重值
if (i<n) {
haffTree[i].weight = weight[i];
}else{
haffTree[i].weight = 0;
}
haffTree[i].parent = 0;
haffTree[i].flag = 0; // flag标记是否已经加入树中
haffTree[i].leftChild = -1;
haffTree[i].rightChild = -1;
}
// 2.构造哈夫曼树的n-1个非叶子结点
// 这里没有做从小到大排序,是在循环中找到最小的两个值,因为数据量很大时做排序浪费时间
for (int i = 0; i<n-1; i++) {
m1 = m2 = MaxValue;
x1 = x2 = 0;
for (j = 0; j<n+i; j++) {
if (haffTree[j].weight < m1 && haffTree[j].flag == 0) {
m2 = m1;
x2 = x1;
m1 = haffTree[j].weight;
x1 = j;
}else if (haffTree[j].weight<m2 && haffTree[j].flag == 0){
m2 = haffTree[j].weight;
x2 = j;
}
}
// x1 和 x2 就是最小的两个节点
// 3.将找到的两个节点
haffTree[x1].parent = n+i;
haffTree[x2].parent = n+i;
// 修改两个字结点的flag标记
haffTree[x1].flag = 1;
haffTree[x2].flag = 1;
// 修改n+i节点的权值 为x1 x2权值和和
haffTree[n+i].weight = haffTree[x1].weight + haffTree[x2].weight;
//
haffTree[n+i].leftChild = x1;
haffTree[n+i].rightChild = x2;
}
}
4. 哈夫曼编码
接下来再聊哈夫曼编码,这里我们仍然借用上图二叉树中ABCDE中的权重来进行研究。
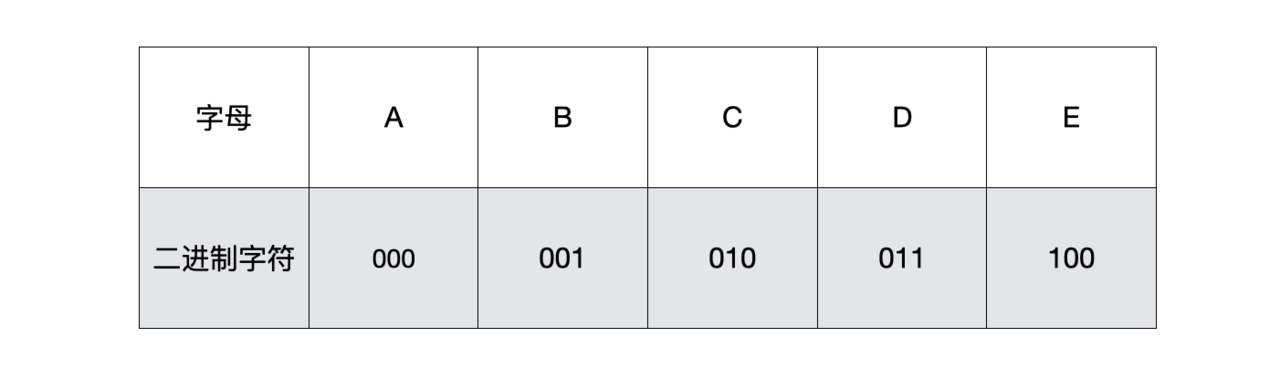
假设我们传递一段电报给朋友,电报内容是“BADCADED”。如果按照下图这样的二进制数据进行编译后,结果为“001 000 011 010 000 011 100 011”24个字符。
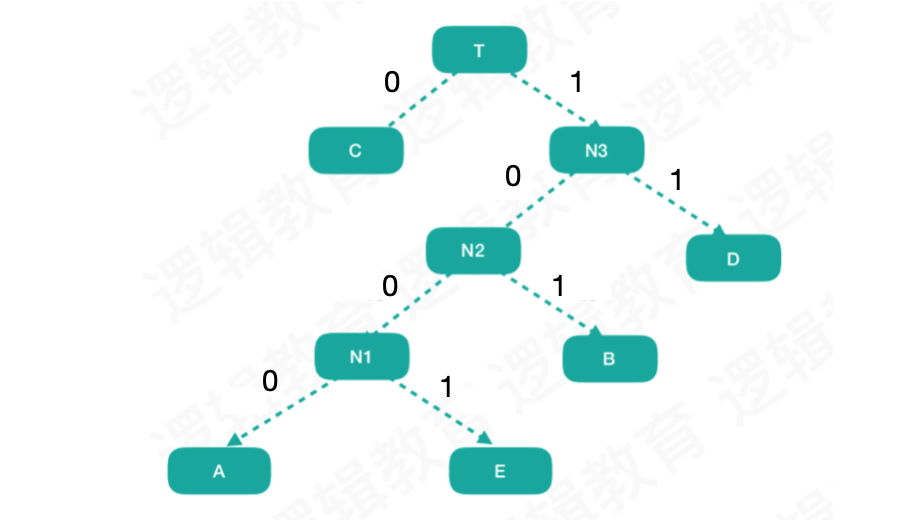
然后我们将上边得到的哈夫曼树的权值左分支改为0,右分支改为1后的哈夫曼树
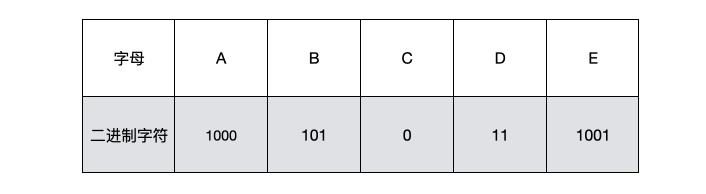
此时,我们对这五个字母从树根到叶子所经过的路径的0或1进行编码,可以得到下表所示的定义:
同样的电报内容再次进行编码,得到结果“101 1000 11 0 1000 11 1001 11”共22个字符,也就是说,数据进行了压缩,随着字符的增加,以及真实字符权重的不同,这种压缩会更加显出其优势。
我们在解码时,也要用到哈夫曼树,即发送方和接收方必须要约定好同样的哈夫曼编码规则。
5. 哈夫曼编码实现
实现代码
// 根据哈夫曼树 构造哈夫曼编码
void HaffmanCode(HaffNode haffTree[], int n, Code haffCode[]){
//1 创建一个结点
Code *cd = (Code *)malloc(sizeof(Code));
int child,parent;
// 2 求n个叶子结点的哈夫曼编码
for (int i = 0; i<n; i++) {
// 从0开始计数
cd->start = 0;
// 取得编码对应权值的字符
cd->weight = haffTree[i].weight;
//当叶子结点i 为孩子结点
child = i;
// 通过孩子结点,在哈夫曼树中找到其双亲结点
parent = haffTree[child].parent;
//由叶子结点向上直到根结点 得到编码 此时编码时逆序的
while (parent != 0) {
if (haffTree[parent].leftChild == child) {
cd->bit[cd->start] = 0;
}else{
cd->bit[cd->start] = 1;
}
//start位置自增
cd->start++;
//当前的双亲结点作为孩子结点 向上继续找
child = parent;
parent = haffTree[child].parent;
}
int temp = 0;
// 将得到的逆序编码进行修正 赋值到haffCode的bit数组中
for (int j = cd->start-1; j>=0; j--) {
temp = cd->start-j-1;
haffCode[i].bit[temp] = cd->bit[j];
}
//把cd中的数据赋值到haffCode[i]中
//保存好haffCode的起始位以及权值
haffCode[i].start = cd->start;
haffCode[i].weight = cd->weight;
}
}