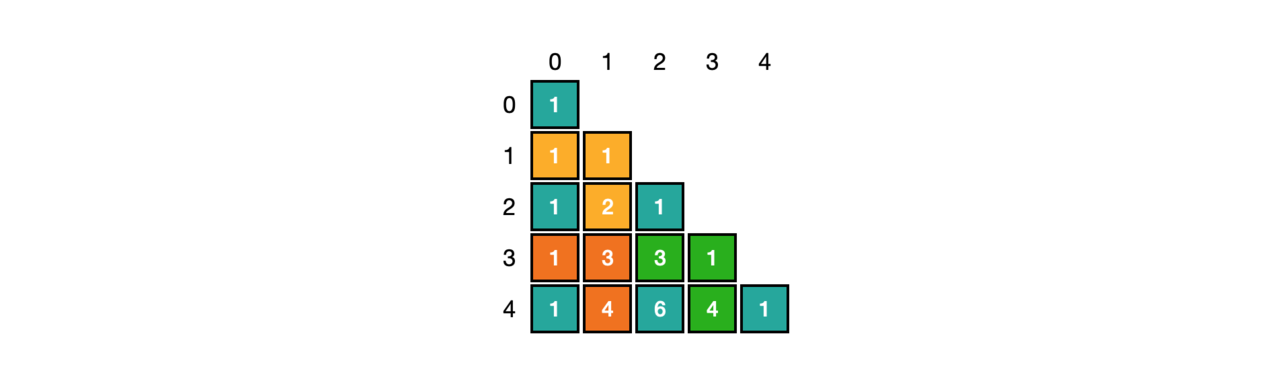
1. 杨辉三角
三角形中的每个数字等于它两肩上的数字相加。
分析:
- 这是一个二维数组,需要循环遍历两次
- 第一次循环行数i,默认可知[i][0] = 1,并且[i][i] = 1;
- 第二次循环列数j,原理可知,每个位置的数字等于两肩的和,可知[i][j] = [i-1][j-1] + [i-1][j];
int** Question(int numRows){
int ** res = (int **)malloc(sizeof(int *)*numRows);
for (int i = 0; i<numRows; i++) {
res[i] = (int *)malloc(sizeof(int)*i+1);
res[i][0] = 1;
res[i][i] = 1;
for (int j = 1; j<i; j++) {
res[i][j] = res[i-1][j-1]+res[i-1][j];
}
}
return res;
}
2.爬楼梯问题
假设你正在爬楼梯。需要n阶你才能到达楼顶。每次你可以爬1或2个台阶。你有多少种不同的方法可以爬到楼顶呢?注意:给定n是一个正整数a
2、1 递归方法
从题目中“每次可以爬1或2个台阶”,我们可以得出递归结束的条件,由此递归方程式f(n-1)+f(n-2)
// 递归法
int Question_1(int n){
if (n < 1) return 0;
if (n == 1) return 1;
if (n == 2) return 2;
return Question_1(n-1)+Question_1(n-2); // 从题目中找出结束的条件,得出递归方程式,
}
2、2 动态规划
动态规划是一种在数学,管理科学,计算机科学,经济学和生物信息中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
动态规划常常适用于有重叠子问题和最优子结构性质的问题,动态规划方法所耗时间往往远少于朴素解法。
动态规划背后的基本思想非常简单。大致上,若要解一个给定问题,我们需要解其不同部分(即子问题),再根据子问题的解得出原问题的解。动态规划往往用于优化递归问题,例如斐波那契数列,如果运用递归的方式来求解会重复计算很多相同的子问题,利用动态规划的思想可以减少计算量。
通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,具有天然剪枝的功能,从而减少计算量:一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时非常有用。
譬如爬楼梯的问题,我们已经知道,当n为1时,我们只有一种方法,当n为2时,我们可以有两种(1+1 或 2)。
那么当n为3时,其实就是n为1 和 n为2时的解的和;
当n为4时,其实就是n为3时的解和n为2时的解的和,其中n为3的解我们已经得到了结果并存储在内存中,依次往下计算&存储直到n。
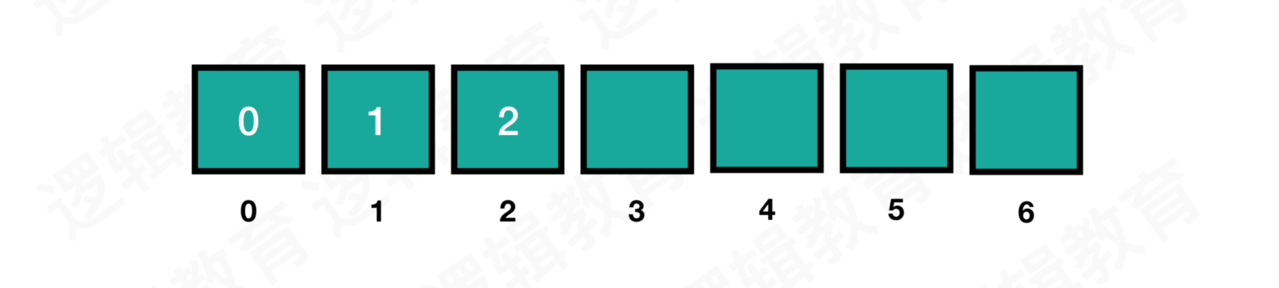
将所有的子问题的解存储在连续的空间里,通过查找前两个空间的值,就可以求出当前的解。
// 动态规划
int Question_2(int n){
if (n==1) {
return 1;
}
int *sum = (int *)malloc(sizeof(int)*n+1); // 开辟一段连续空间
sum[0] = 0;
sum[1] = 1;
sum[2] = 2;
for (int i = 3; i<=n; i++) {
sum[i] = sum[i-1]+sum[i-2]; // 从前两块空间的值得出当前的解
}
return sum[n];
}
从外表看,递归法得出的方程式f(n) = f(n-1)+f(n-2) 和 动态规划似乎有点相像,但其实是有根本不同的:
- 递归:将所求的n向前求解直到结束条件,
- 动态规划法:是从已知的子问题解向后求解直到n。
而且,动态规划法会多开辟一段内存空间,递归则会多占用栈空间。
3.括号匹配问题
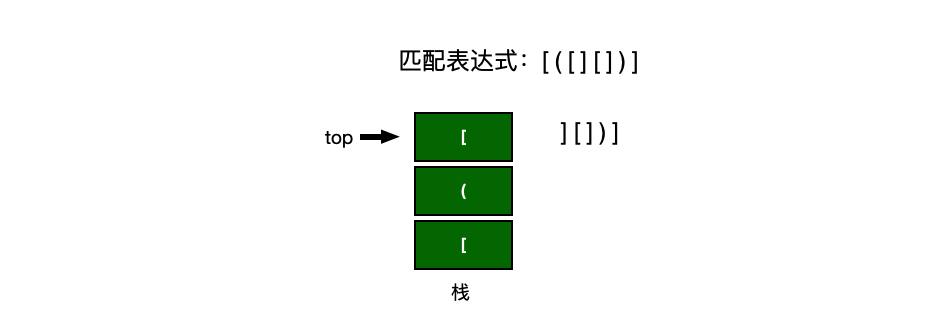
假设表达式中允许包含两种括号:圆括号与方括号,其嵌套顺序随意,即([]())或者[([][])]都是正确的.而这[(]或者(()])或者([())都是不正确的格式.检验括号是否匹配的方法可用”期待的急迫程度”这个概念来描述.例如,考虑以下括号的判断: [([][])]
3、1 解法分析
涉及到不断对比,可以使用栈思想来解决。
- 将第0个元素压入栈,遍历[1 , strlen(data)]
- 取出栈顶元素,如果栈顶元素是‘(’ 或者 ‘[’ ,看遍历的结果data[i]是否是对应的‘)’或者’]’,对应则出栈,否则将遍历的结果入栈
- 最终判断栈是否为空,空表示匹配成功,否则就是失败
Status Question(char *str,linkStackList stack){
PushStack(&stack, str[0]); // 第一个字符放到栈底
for (int i = 1; i<strlen(str); i++) {
char top = GetTop(stack); // 取出栈顶元素,进行匹配
switch (top) {
case '[':
if (str[i]==']') {
PopStack(&stack); // 匹配成功,出栈
}else{
PushStack(&stack, str[i]); // 匹配失败,将遍历的str[i]入栈
}
break;
case '(':
if (str[i]==')') {
PopStack(&stack);
}else{
PushStack(&stack, str[i]);
}
break;
default:
return ERROR; // 字符不合法
break;
}
}
if (stack.count == 0) {
printf("匹配正确\n");
DestoryStack(&stack);
return OK;
}else{
printf("匹配失败\n");
DestoryStack(&stack);
return ERROR;
}
}
4.进制转换
十进制转八进制
void Question(int N){
SqStack S;
SElemType e;
//1.初始化一个空栈S
InitStack(&S);
//2.
while (N) {
PushData(&S, N%8); // 将输入的十进制数据求余的结果压入栈
N = N/8; // N 重新赋值为与8的商 ,循环计算
}
//3.
while (!StackEmpty(S)) {
Pop(&S, &e); // 输出结果
printf("%d\n",e);
}
}
5.字符串编码
字符串编码(LeetCode-中等)
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded. _string], 表示其中方括号内部的encoded_ string 正好重复k次。
注意k保证为正整数。你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,
且输入的方括号总是符合格式要求的。此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数k,例如不会出现像3a或2[4]的输入。
例如:
s = “2[a]2[bc]”,返回”aabcbc” .
s = “3[a2[c]]”,返回”accaccacc”.
s = “2[abc]3[cd]ef”,返回”abcabccdcdcdef”.
解题思路:
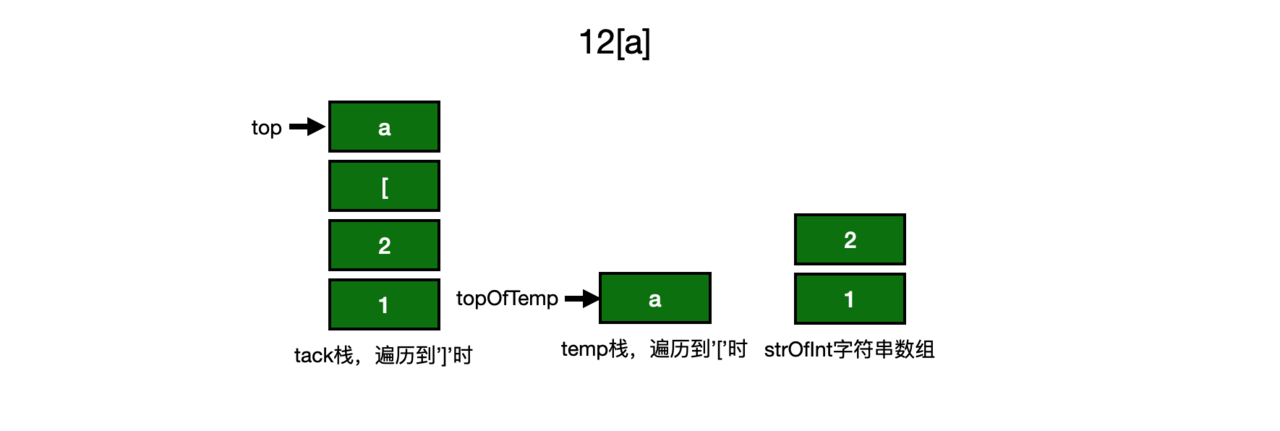
以s = 12[a]为例:
1、 遍历s,如果当前字符不等于方括号 ‘ ] ‘ ,入stack栈中,stack=‘12[a’ ;
2、 遍历stack栈,不等于方括号 ‘ [ ‘, 入temp栈中,temp=‘a’,top–,去掉stack中的字符;
3、 top-1,剔除掉当前stack中的’ [ ‘,遍历找到下限top==-1或top指向的非数字,遍历这个范围,将数字保存strOfInt字符串数组中
4、 strOfInt转换为Int类型,将temp中的字符复制strOfInt份
char * Question(char *s){
int len = (int)strlen(s);
int stackSize = 50;
char *stack = (char *)malloc(sizeof(char)*stackSize); // ‘]’前元素入栈
int top = -1; // stack的指针
for (int i = 0; i<len; i++) {
// 这里要注意:S字符串的长度是否超过栈长度,超过需要扩容
if (top == stackSize-1) {
stack = realloc(stack, sizeof(char) * (stackSize+=50));
}
if (s[i] != ']') {
top++;
stack[top] = s[i];
printf("没有遇到']'之前# top = %d 栈里存储的有:%s\n",top,stack);
}else{ // 当等于']'时 , 开始循环栈stack 获取字符‘a’,我们只需要找到'['就够了
int tempSize = 10;
char *temp = (char *)malloc(sizeof(char) * tempSize); // 过滤的字符放到这里
int topOfTemp = -1; // temp的指针
printf("开始从栈中查找字符之前,top = %d\n",top);
while (stack[top] != '[') {
// 这里同样注意 字符的长度是否超过temp栈 超过同样扩容
if (topOfTemp > tempSize-1) {
temp = realloc(temp, sizeof(char)*(tempSize+=10));
}
topOfTemp++;
temp[topOfTemp] = stack[top];
top--;
}
printf("开始从栈中查找字符之后,top = %d\n",top);
// stack循环结束后 剩下 '12[', 将stack的top--,就可以把其中的'['去除,接下来开始找数字
char strOfInt[11]; // 数字字符串, 注意:如果大于1位的情况就处理
int curTop = top; // 记录当前的top
printf("开始获取数字,数字的上限在curTop = %d\n",curTop);
top--; // 剔除 '['
// 开始遍历剩下的 stack栈
// 上限是curTop 下限是栈指针指向空 或者 stack[top]不为数字 ,因为字符串有可能有多个'[ ]'
while (top != -1 && stack[top]>='0' && stack[top]<='9') {
top--;
}
// 循环结束后,top即为我们找到的下限,那么要获取的数字就在 [top+1 , curTop]
printf("开始获取数字,数字的下限在top = %d\n",top);
for (int j = top+1; j<curTop; j++) {
strOfInt[j-(top+1)] = stack[j];
}
// 为字符串数组strOfInt添加一个字符结束符'\0';
strOfInt[curTop-(top+1)] = '\0';
// 将strOfInt字符串转换成整数 atoi函数;
// 将temp栈中的字符 复制strOfInt份到stack中
int curNum = atoi(strOfInt);
for (int k = 0; k<curNum; k++) {
int kk = topOfTemp; // 注意:循环curNum时,将topOfTemp赋值给kk,对kk进行--操作,不可以直接操作topOfTemp指针
while (kk != -1) {
// stack到达存储上限,进行扩容
if (top == stackSize-1) {
stack = realloc(stack, sizeof(char)*(stackSize+=50));
}
top++;
stack[top] = temp[kk];
kk--;
}
}
free(temp);
temp = NULL;
}
}
char *result = realloc(stack, sizeof(char)*(top+1));
result[++top] = '\0';
free(stack);
return result;
}
做算法题的方法:
1、 充分阅读题目.了解题目背后的关键意思;
2、 分析题目,涉及到哪些数据结构,对问题进行分类. 到底属于链表问题, 栈思想问题, 字符串问题,二叉树问题,图相关问题,排序问题; 与你之前所接触过的算法题有没有类似,找到问题的解题思路
3、 实现算法. 在算法的实现的过程,并不是一蹴而就, 肯定是需要不断的调试,修改的;
4、 验证算法正确性
5、 找到题源, 看其他的开发者对齐的解决思路.
6、 找到题解建议之后, 对于其他优秀思路,分析它的优势,并且学习它的思路.并且写成其他解法的代码
7、 算法题的解题能力来自于2点: 对于数据结构与算法核心问题是否夯实 + 是否有足够多且足够耐心的积累;
ps.栈思想的应用,是指利用栈的特性先进先出,那么什么问题适合用栈思想解决?
- 数据是线性的
- 问题中常常涉及到数据的来回比较,匹配。例如括号匹配,每日温度等
- 问题中涉及数据的转置。例如进制问题,链表倒叙打印问题
注意:栈思想只是一个解决的参考思想,并不是万能的,适用于以上这样的情况下来解决问题,利用栈思想解决问题时,首先需要透彻的解析问题之后,找到问题解决的规律,才能使用它解决。思想只是指导作用,具体问题还需具体分析,在基本思想上寻找解决办法