题目:
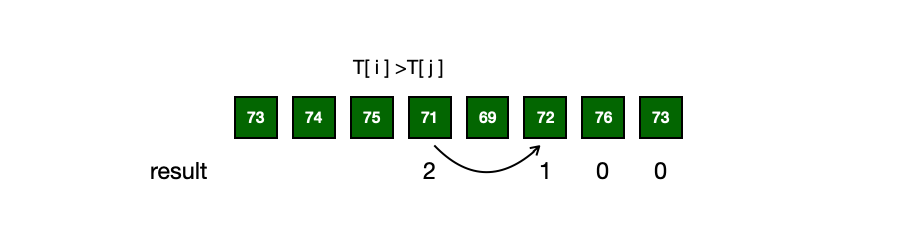
根据每日气温列表,请重新生成一个列表,对应位置的输入是你需要再等待多久温度才会升高超过该日的天数。如果之后都不会升高,请在该位置0来代替。例如,给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73],你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。
提示:气温 列表长度的范围是 [1, 30000]。每个气温的值的均为华氏度,都是在 [30, 100] 范围内的整数。
分析:
实际上就是找当前元素 从[i,TSize] 找到大于该元素时. 数了几次. 首先最后一个元素默认是0,因为它后面已经没有元素了.
1. 暴力法
解题方法:直接循环两次进行对比
注意点:
- i 和 j 的循环范围需要注意 两者是不一样的
因为最后一个 默认是0 i的循环范围应该是 [0 – TSize-1]
而j的范围应该是i之后的第一个位置开始 ,一直到最后TSzie,
- 进行对比前,可以先过滤掉相等的情况
如果两者对比相等,需要判断后者result[i-1]==0?
int * Question_11(int *T, int TSize, int *returnSize){
int *result = (int *)malloc(sizeof(int)*TSize);
*returnSize = TSize;
result[TSize-1] = 0; // 默认最后一个为0
for (int i = 0; i<TSize-1; i++) {
if (i > 0 && T[i] == T[i-1]) {
result[i] = result[i-1]==0 ? 0:result[i-1]-1; // 此处要注意!!!
}else{
for (int j = i+1; j<TSize; j++) {
if (T[i]<T[j]) {
result[i] = j-i;
break;
}
if (j == TSize-1) {
result[i] = 0;
}
}
}
}
return result;
}
2. 跳跃对比
解题方法:
- 换个思维考量,从右向左倒着遍历,T[i]对比后边的T[j]
- 当T[i]>T[j]时,因为result中保存的是从右向左的数据,即result[j]我们是知道的,我们就可以直接使用T[i]与result[j]指向的值进行跳跃对比,从而减少遍历对比的次数
- 当T[i]<T[j]时,那么如上result[i] = j-i;
注意:
1、最后一个result[TSize-1]默认是0
2、当result[j] == 0时,则表示,后边没有比T[j]大的数字,那么当T[i]也不大于T[j]时,result[i]也会是0;
int *Question_2(int *T, int TSize, int * returnSize){
int *result = (int *)malloc(sizeof(int)*TSize);
*returnSize = TSize;
result[TSize-1] = 0; // 默认最后一个为0
// 从右向左遍历 直到i==0,
for (int i = TSize-2; i>=0; i--) {
// j+=result[j] 即为跳跃到 当前比下一个位置大的值 然后T[i]再与它对比,中间的值可以直接跳过
for (int j = i+1; j<TSize; j+=result[j]) {
if (T[i] < T[j]) {
result[i] = j-i;
break;
}else{
// T[i] >= T[j]时, 判断当result[j]为0时,即j后边的数据都是小于result[j],那么T[i]肯定也是0,可以不用再跳跃,直接break
if (result[j] == 0) {
result[i] = 0;
break;
}
}
}
}
return result;
}
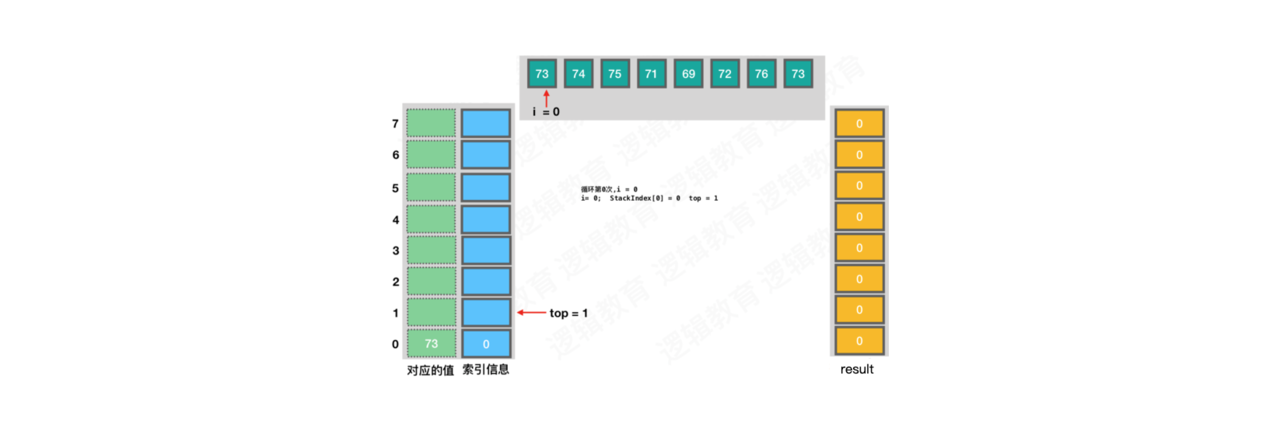
3.栈思想解决
解题方法:
利用栈思想,初始化一个存储元素下标的stack_index数组,result结果数组,
遍历整个温度数组,
1>stack_index栈中没有元素,那么新元素的下标入栈中
2>下一个数值大于栈顶top对应的数值,则出栈,保存两个数值的下标差值,就是result的结果
3>若不大于的话,将下一个数值的下标入栈,继续循环对比
4>如果直到循环结束,那么栈中数值的result对应的都是0,因为没有找到比他们大的值
int *Question_3(int *T, int TSize,int *returnSize){
int *result = (int *)malloc(sizeof(int)*TSize);
int *stack_index = (int *)malloc(sizeof(int)*TSize);
*returnSize = TSize;
result[TSize-1] = 0;
int top = 0; // 栈顶指针
int tIndex;
for (int i = 0; i<TSize; i++) { // 结果赋初值0
result[i] = 0;
}
for (int i = 0; i<TSize; i++) {
while (top>0 && T[i] > T[stack_index[top-1]]) {
tIndex = stack_index[top-1]; // 栈顶所存储的下标
result[tIndex] = i - tIndex;
top--;
}
stack_index[top] = i;
top++;
}
return result;
}
ps:栈思想只是解决方法的一种方向,并不是说解决问题时,栈思想是最完美的解法。