1. 树
定义:
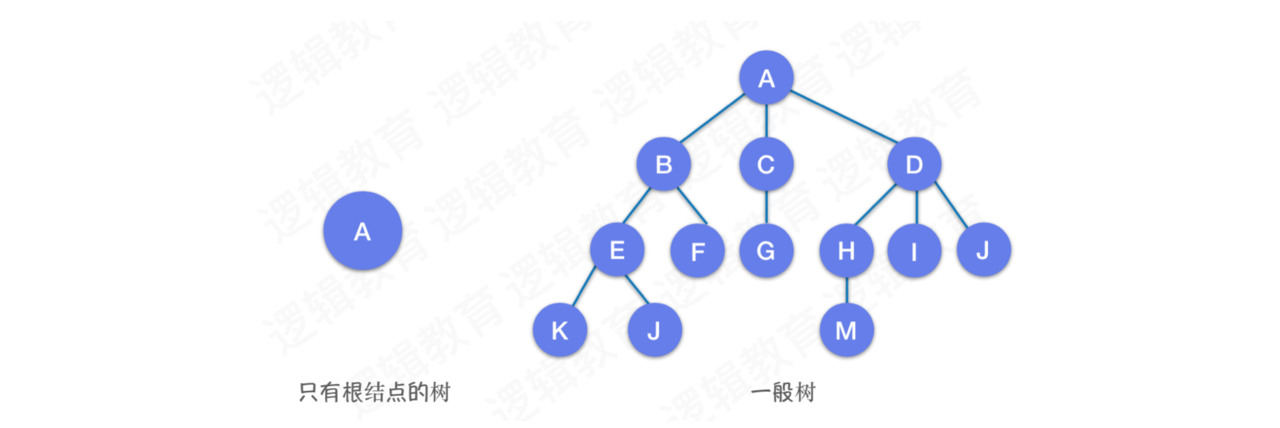
树是一种表示了“一对多”关系的数据结构,例如说军队中,一个班长对多个士兵,一个排长对多个班长…
树是n(n>=0)个结点的有限集,n=0 时称为空树。
在任意一棵非空树中:
1>有且仅有一个特定的称为根(root)的结点;
2>当 n>1 时,其余结点可分为m(m>0)个互不相交的有限集T1,T2…..Tm,其中每一个集合本身又是一棵树,称之为根的子树
度:结点拥有的子树的数量称为结点的度:B结点的度为2(E,F),C结点的度为1(G)…
内部结点:子树的根结点
叶结点:度为0的结点称为叶结点或终端结点
树的高度:叶结点到根结点的最长的边数
树的深度:根结点到叶结点的最长的边数
结点间的关系:
- 结点的子树的根,称为该结点的孩子结点,该结点也是孩子结点的双亲结点;
- 同一双亲结点下的孩子结点为兄弟结点
- 该结点下所有子树的任一结点为该结点的子孙结点
结点的层级:从根开始定义,根为第一层,根的孩子为第二层…
结点的次序:从左向右
2. 二叉树
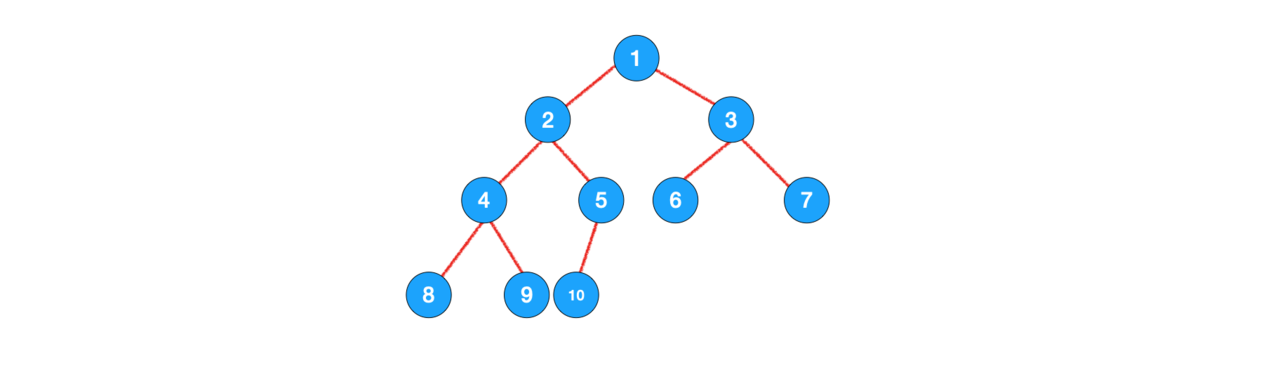
二叉树由一个根结点和两棵互不相交的子树组成,两个子树分别称为左子树,右子树。
特点:
- 每个结点最多有两棵子树
- 左子树和右子树是有顺序的,次序不能颠倒
- 即使树中某结点只有一个子树,也要区分它是左子树还是右子树(如上,10是5的左子树)
特殊二叉树:
- 斜树:所有结点都只有左子树或者右子树,那么分别称之为左斜树/右斜树
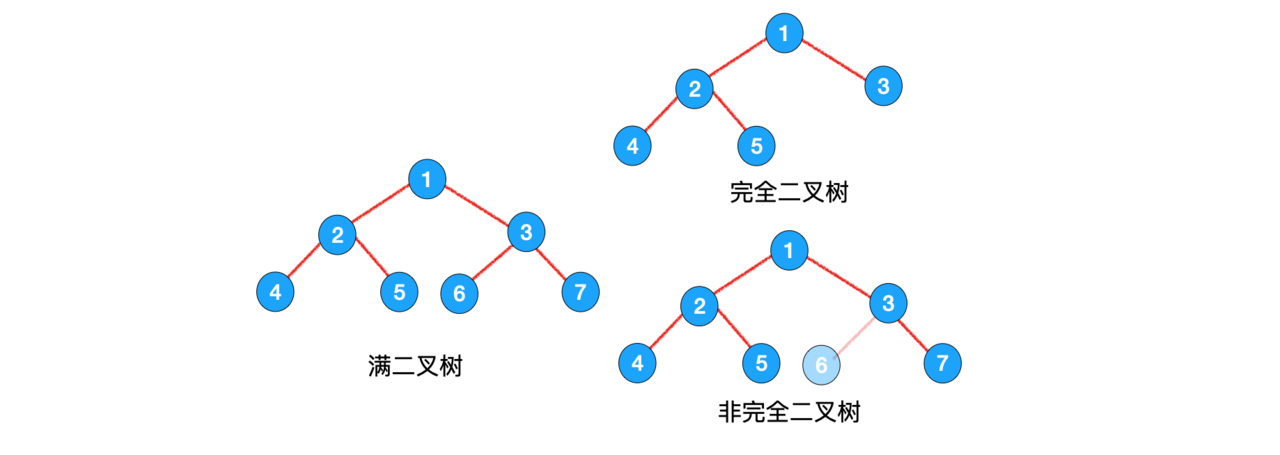
- 满二叉树:所有的结点都有两个子树,并且叶子结点都在同一层。(整体看来是左右对称的)
- 完全二叉树:完全二叉树的所有结点与同样深度的满二叉树,按照
层序编号相同的结点,是一一对应的。
满二叉树一定是一棵完全二叉树,但是完全二叉树不一定是满二叉树
3. 二叉树的顺序存储
顺序存储结构,对于树这种一对多的关系结构,实现起来是比较困难,但是二叉树由于其特殊性,使得使用顺序存储结构也可以实现。
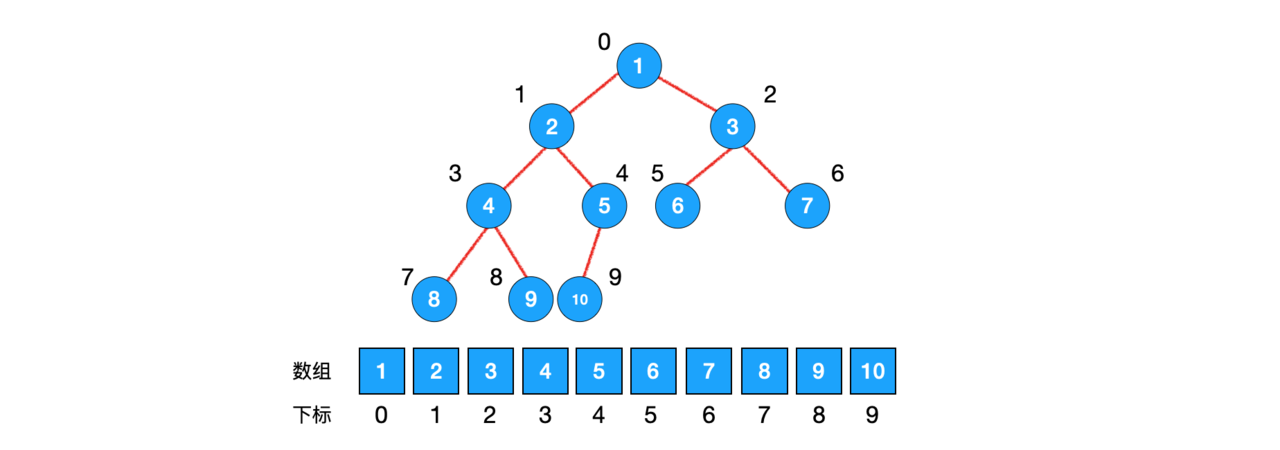
二叉树的顺序存储结构就是用一维数组存储二叉树中的结点。
上图中由于完全二叉树的严格性,所以可以使用顺序存储来表现二叉树的结构;
对于一般二叉树,尽管层序编号不能反映逻辑关系,但是也可以将其按照完全二叉树编号,在不存在的结点设置为“^”(设置随意不冲突就好)。
- 构造设计
#define MAX_TREE_SIZE 100 /* 二叉树的最大结点数 */
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */
typedef int CElemType; /* 树结点的数据类型,目前暂定为整型 */
typedef CElemType SqBiTree[MAX_TREE_SIZE]; /* 0号单元存储根结点 */
CElemType NIL = 0; /*设整型以0为空 或者以 INT_MAX(65535)*/
// 结点位置信息
typedef struct {
int level; // 结点层
int order; // 本层的序号(按照满二叉树给定序号规则)
}Position;
- 二叉树的基本信息
// 构造空的二叉树 因为T是固定数组,不会改变.
Status InitBiTree(SqBiTree T){
for (int i = 0; i<MAX_TREE_SIZE; i++) {
T[i] = NIL;
}
return OK;
}
// 在顺序存储结构中,清除树和构造一个树,方法代码是一样的
// 如果想要两个函数的结果一样,但是目的不同,可以这样
#define ClearBiTree InitBiTree
// 按层序次序给二叉树赋值
Status CreateBiTree(SqBiTree T){
int i = 0;
while (i<10) { // 给二叉树的前十位赋值
T[i] = i+1;
printf("二叉树赋值 %d \n",T[i]);
// 过滤树中错误的结点,当结点不为空 且无双亲结点,
if (i!=0 && T[(i+1)/2-1] == NIL && T[i] != NIL) {
printf("出现无双亲的非跟结点%d",T[i]);
exit(ERROR);
}
i++;
}
// 其余的结点赋值NIL
while (i<MAX_TREE_SIZE) {
T[i] = NIL;
i++;
}
return OK;
}
// 判断是否为空
Status BiTreeEmpty(SqBiTree T){
if (T[0] == NIL) {
return TRUE;
}
return FALSE;
}
// 获取二叉树的深度
/*
从后向前遍历获取最后一个结点的位置
计算2的次幂,获取深度
*/
Status BiTreeDepth(SqBiTree T){
int j = -1;
int i;
for (i = MAX_TREE_SIZE; i>=0; i--) {
if (T[i] != NIL) {
break;
}
}
do {
j++;
} while (powl(2, j) <= i);
return j;
}
// 返回处于位置e的结点值
CElemType GetValue(SqBiTree T,Position e){
/*
Position.level - 结点层,表示第几层
Position.order - 本层的序号
*/
// 找到层序
printf("%d\n",(int)pow(2, e.level-1));
printf("%d\n",e.order);
return T[(int)pow(2, e.level-1)+e.order-2];
}
// 获取根结点的值
Status GetRoot(SqBiTree T,CElemType *e){
if (BiTreeEmpty(T)) {
return ERROR;
}
*e = T[0];
return OK;
}
// 给位置e的结点赋值
Status Assign(SqBiTree T,Position e,CElemType value){
// 找到e在数组中的具体位置索引
int i = (int)powl(2, e.level-1)+e.order-2;
// 判错 双亲结点是否为空
if (value != NIL && T[(i+1)/2-1] == NIL) {
return ERROR;
}
//给双亲赋空值但是有叶子结点
if (value == NIL && (T[i*2+1] != NIL || T[i*2+2] != NIL)) {
return ERROR;
}
T[i] = value;
return OK;
}
// 获取某个值v的双亲结点的值
CElemType GetParent(SqBiTree T,CElemType v){
if (T[0] == NIL) { // 空树
return ERROR;
}
// 注意 找有双亲的结点 需要从1开始查找
for (int i = 1; i<MAX_TREE_SIZE; i++) {
if (T[i] == v) {
int index = (i+1)/2-1;
return T[index];
}
}
return NIL;
}
// 获取某个节点的左孩子
CElemType GetLeftChild(SqBiTree T,CElemType v){
if (T[0] == NIL) {
return NIL;
}
for (int i = 0; i<MAX_TREE_SIZE; i++) {
if (T[i] == v) {
int index = 2*i+1;
return T[index];
}
}
return NIL;
}
// 获取某个节点的右孩子
CElemType GetRightChild(SqBiTree T,CElemType v){
if (T[0] == NIL) {
return NIL;
}
for (int i = 0; i<MAX_TREE_SIZE; i++) {
if (T[i] == v) {
int index = 2*i+2;
return T[index];
}
}
return NIL;
}
// 获取某个节点的左兄弟 需要注意 这个节点是否就是左结点
CElemType GetLeftSibling(SqBiTree T,CElemType v){
if (T[0] == NIL) {
return NIL;
}
for (int i = 0; i<MAX_TREE_SIZE; i++) {
if (T[i] == v&&i%2 == 0) {
int index = i-1;
return T[index];
}
}
return NIL;
}
// 获取某个节点的右兄弟 需要注意 这个节点是否就是右结点
CElemType GetRightSibling(SqBiTree T,CElemType v){
if (T[0] == NIL) {
return NIL;
}
for (int i = 0; i<MAX_TREE_SIZE; i++) {
if (T[i] == v&&i%2 == 1) {
int index = i+1;
return T[index];
}
}
return NIL;
}
- 二叉树遍历
// 层序遍历 直接循环遍历数组就够了
void LevelOrderTraverse(SqBiTree T){
int i = MAX_TREE_SIZE-1;
// 找到树的最后一个非空节点
while (T[i] == NIL) {
i--;
}
printf("层序遍历\n");
for (int j = 0; j<=i; j++) {
if (T[j] !=NIL) {
printf("%d ",T[j]);
}
}
printf("\n");
}
//前序遍历 先序遍历
void PreTraverse(SqBiTree T, int e){
printf(" %d ",T[e]);
if (T[2*e+1] != NIL) {
PreTraverse(T, 2*e+1);
}
if (T[2*e+2] != NIL) {
PreTraverse(T, 2*e+2);
}
}
// 中序遍历
void MidTraverse(SqBiTree T,int e){
if (T[2*e+1] != NIL) {
MidTraverse(T, 2*e+1);
}
printf(" %d ",T[e]);
if (T[2*e+2] != NIL) {
MidTraverse(T, 2*e+2);
}
}
// 后序遍历
void PostTraverse(SqBiTree T,int e){
if (T[2*e+2] != NIL) {
PostTraverse(T, 2*e+2);
}
if (T[2*e+1] != NIL) {
PostTraverse(T, 2*e+1);
}
printf(" %d ",T[e]);
}
4. 二叉树的链式存储
当然,在一些极端特殊的情况下,二叉树使用顺序存储是非常麻烦,也非常浪费空间的,例如说,当二叉树是右斜树时,需要在确实的位置补空占位,这时候我们可以使用链式存储结构来实现。
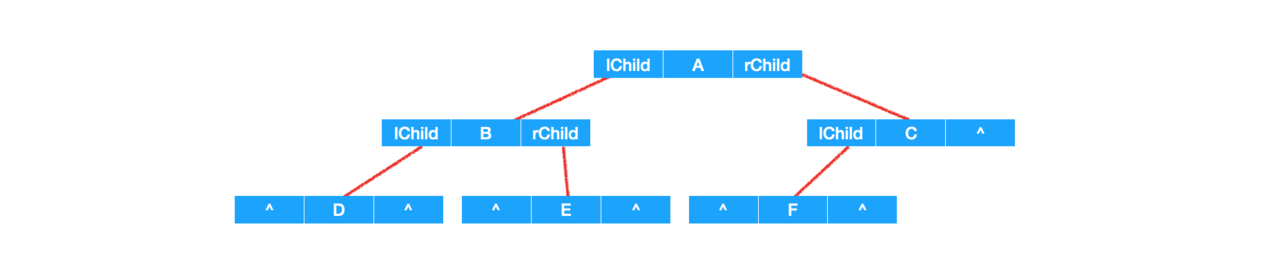
二叉树每个结点最多有两个孩子结点,可以设计称一个数据域和两个指针域,这样的链表也叫二叉链表。
- 链式存储的二叉树结构
/* 存储空间初始分配量 */
#define MAXSIZE 100
/* Status是函数的类型,其值是函数结果状态代码,如OK等 */
typedef int Status;
typedef char CElemType;
CElemType NIL = ' '; // 空格符为空
#pragma mark--二叉树构造
int indexs = 1;
typedef char String[24]; /* 0号单元存放串的长度 */
String str;
typedef struct BiTNode{
CElemType data; // 结点数据
struct BiTNode *lChild, *rChild; // 左右孩子结点的指针
}BiTNode,*BiTree;
- 基本操作
// 将字符串分配到字符数组
Status StrAssign(String S, char *chars){
int i;
if (strlen(chars) > MAXSIZE) {
return ERROR;
}
S[0] = strlen(chars); //0号存放串的长度
for (i = 1; i<=S[0]; i++) {
S[i] = *(chars+i-1);
}
return OK;
}
// 构造一个空的二叉树
Status InitBiTree(BiTree *T){
*T = NULL;
return OK;
}
// 销毁二叉树
void DestroyBiTree(BiTree *T){
if (*T) {
if ((*T)->lChild) {
DestroyBiTree(&(*T)->lChild);
}
if ((*T)->rChild) {
DestroyBiTree(&(*T)->rChild);
}
free(*T);
*T = NULL;
}
}
// 创建二叉树
void CreateBiTree(BiTree *T){
CElemType ch;
ch = str[indexs++]; // index 从1开始计算 获取第一个字符
if (ch == '#') {
*T = NULL;
}else{
// 创建新的结点
*T = (BiTree)malloc(sizeof(BiTNode));
if (!*T) {
exit(OVERFLOW);
}
(*T)->data = ch;
CreateBiTree(&(*T)->lChild); // 左子树
CreateBiTree(&(*T)->rChild); // 右子树
}
}
// 二叉树是否为空
Status BiTreeEmpty(BiTree T){
if (T) {
return FALSE;
}
return TRUE;
}
// 二叉树的深度 找到左右子树的最深度 判断哪个最大
int BiTreeDepth(BiTree T){
int i,j;
if (!T) {
return 0;
}
if (T->lChild) {
i = BiTreeDepth(T->lChild);
}else{
i = 0;
}
if (T->rChild) {
j = BiTreeDepth(T->rChild);
}else{
j = 0;
}
return i>j?i+1:j+1;
}
// 获取二叉树的根
CElemType GetRoot(BiTree T){
if (BiTreeEmpty(T)) {
return NIL;
}
return T->data;
}
- 链式二叉树的遍历
// 前序递归遍历T
void PreOrderTraverse(BiTree T)
{
if(T==NULL)
return;
printf("%c ",T->data);/* 显示结点数据,可以更改为其它对结点操作 */
PreOrderTraverse(T->lChild); /* 再先序遍历左子树 */
PreOrderTraverse(T->rChild); /* 最后先序遍历右子树 */
}
// 中序递归遍历T
void InOrderTraverse(BiTree T)
{
if(T==NULL)
return ;
InOrderTraverse(T->lChild); /* 中序遍历左子树 */
printf("%c ",T->data);/* 显示结点数据,可以更改为其它对结点操作 */
InOrderTraverse(T->rChild); /* 最后中序遍历右子树 */
}
// 后序递归遍历T
void PostOrderTraverse(BiTree T)
{
if(T==NULL)
return;
PostOrderTraverse(T->lChild); /* 先后序遍历左子树 */
PostOrderTraverse(T->rChild); /* 再后序遍历右子树 */
printf("%c ",T->data);/* 显示结点数据,可以更改为其它对结点操作 */
}