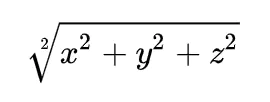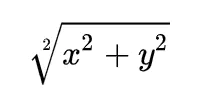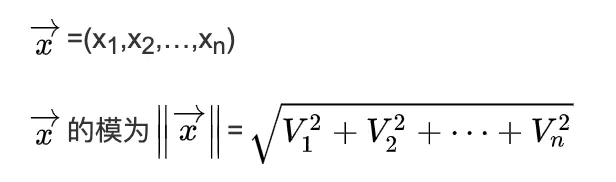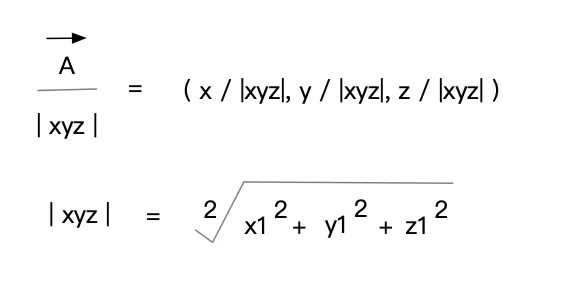在我们OpenGL中涉及到图形变换的时候经常会运用到向量/矩阵的运算。今天我们就来了解下OpenGL中的向量、矩阵。
一、向量
1.标量和向量
- 标量:只要大小,没有方向的量。 比如:温度、质量、密度、长度等,标量的运算遵循代数的加减法则。
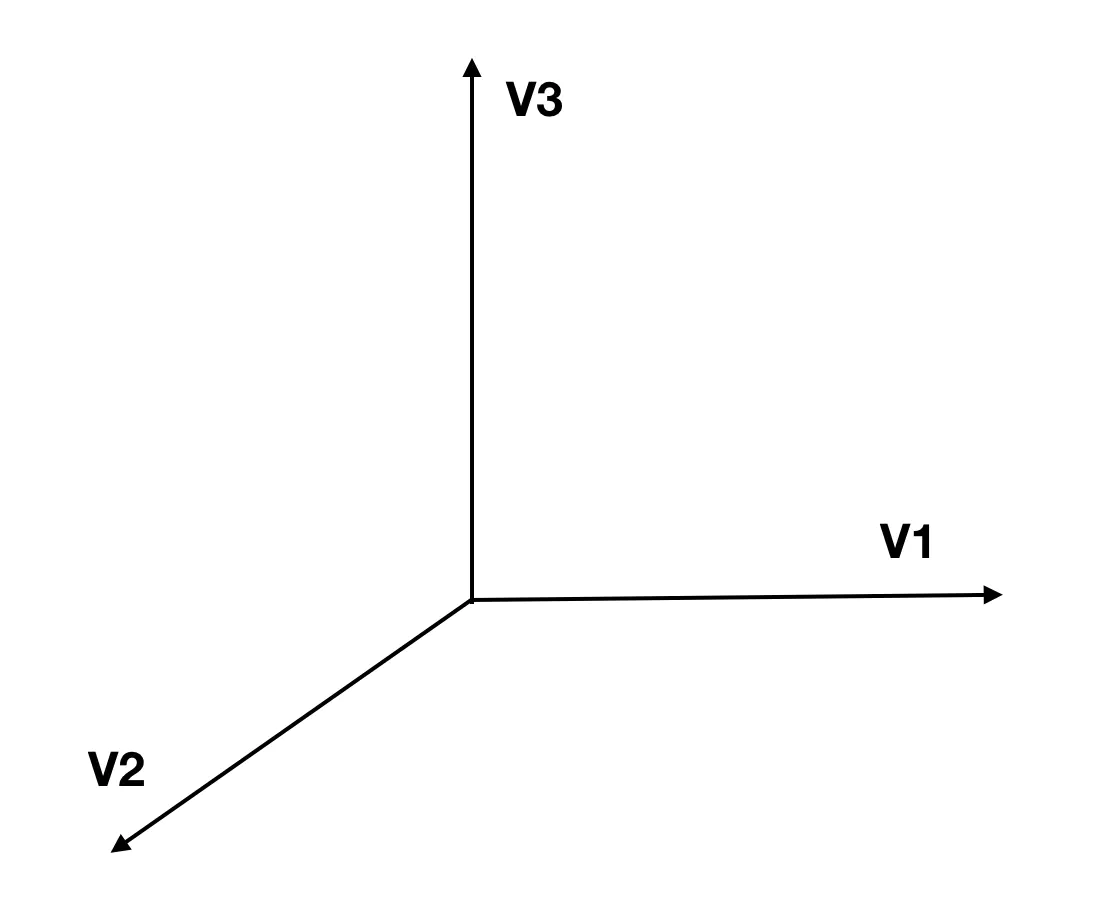
- 向量/矢量:既有大小,也有方向的量。 例如:加速度、位移、力、冲量、动量、电场强度、磁场强度,向量的运算并不遵循一般的代数法则,在相加减时它们遵从几何运算法则(平行四边形法则、三角形法则)。矢量常用带有箭头的直线段表示。线段的长度代表矢量大小,箭头代表矢量的方向。
2.向量的模:向量的长度或者大小即称为向量的模。
- 空间向量
(x,y,z),其中x,y,z分别是三轴上的坐标,模长是: -
平面向量
(x,y),模长是: -
类似的n维向量的模:
3.单位向量和向量单位化
- 单位向量:即向量的长度为1.
- 向量单位化:如果一个向量不是单位向量,可以通过单位化将其转化为单位向量,即 非零向量除以向量的模。
4.OpenGL中的向量:
在OpenGL中GLTools库中有⼀个组件叫Math3d,其中包含了大量好用的OpenGL⼀致的3D数学和数据类型。 math3d库,有2个数据类型,能够表示一个三维或者四维向量。
M3DVector3f可以表示⼀个三维向量量(x,y,z),M3DVector4f则可以表示⼀个四维向量(x,y,z,w). 在典型情况下,w坐标设为1.0。x,y,z值通过除以w,来进⾏缩放。⽽除以1.0则本质上不改变x,y,z值。
//三维向量量/四维向量量的声明
typedef float M3DVector3f[3];
typedef float M3DVector4f[4];
//声明⼀个三维向量 M3DVector3f:类型 vVector:变量量名
M3DVector3f vVector;
//声明⼀一个四维向量量并初始化⼀一个四维向量量
M3DVector4f vVertex = {0,0,1,1};
//声明⼀一个三分量量顶点数组,例例如⽣生成⼀一个三⻆角形 //
M3DVector3f vVerts[] = {
-0.5f,0.0f,0.0f,
0.5f,0.0f,0.0f,
0.0f,0.5f,0.0f
};
5.向量的点乘和叉乘:
- ######点乘(
dot product): 向量可以进行加法、减法计算. 但是向量里有⼀个在开发中使⽤价值⾮高的操作,叫做 “点乘(dot product)” 。点乘只能发⽣在2个向量之间进⾏。
前提条件: 2个向量必须为单位向量; 动作: 2个三维向量之间进行点乘 结构: 返回⼀个[-1,1]范围的值. 这个值其实就是夹角的cos值(余弦值)。
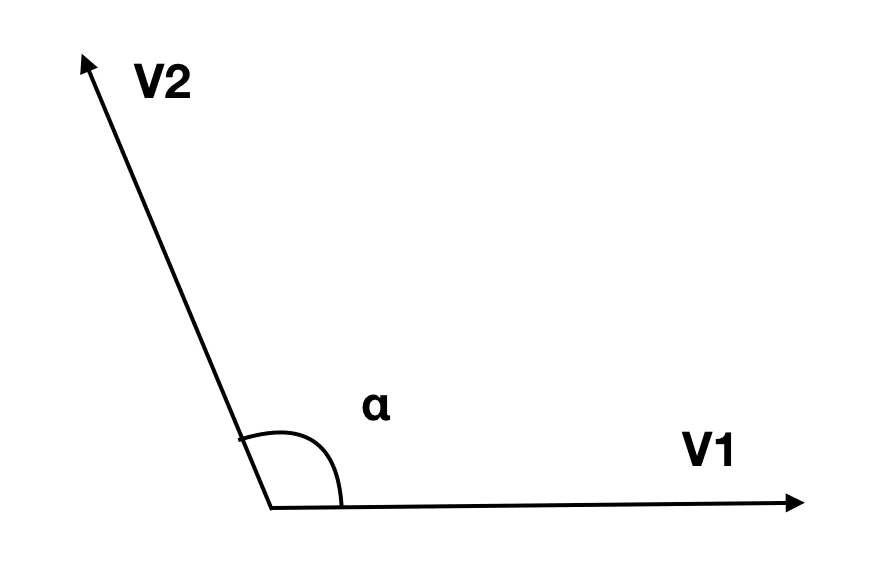
OpenGL中向量的点乘: math3d库中提供了了关于点乘的 API:
//1.m3dDotProduct3 函数获得2个向量之间的点乘结果;
float m3dDotProduct3(const M3DVector3f u,const M3DVector3f v);
//2.m3dGetAngleBetweenVector3 即可获取2个向量之间夹角的弧度值;
float m3dGetAngleBetweenVector3(const M3DVector3f u,const M3DVector3f v);
-
叉乘(
cross product):向量之间的叉乘(
cross product) 也是在业务开发⾥⾮常有用的一个计算⽅式; 2个向量之间叉乘就可以得到另外⼀个向量,新的向量会与原来2个向量定义的平⾯垂直. 同时进⾏叉乘,不必为单位向量;前提: 2个普通向量 动作: 向量与向量叉乘 结果: 向量(垂直于原来2个向量定义的平⾯的向量)
OpenGL中的叉乘:
math3d库中提供了关于叉乘的API:
//.m3dCrossProduct3 函数获得2个向量之间的叉乘结果得到⼀一个新的向量
void m3dCrossProduct3(M3DVector3f result,const M3DVector3f u ,const
M3DVector3f v);
二、矩阵
在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数,最早来自于方程组及常数所构成的方阵。 在OpenGL中,假设在空间有⼀个点.使⽤x,y,z描述它的位置。此时让其围绕任意位置旋转⼀定⻆度后,我们需要知道这个点的新的位置。此时需要通过矩阵进⾏计算。 因为新的位置的x不单纯与原来的x还和旋转的参数有关,甚⾄于y和z坐标有关。 矩阵不仅可以有多行多列,只有一行一列也是可以的,只有一行或者一列的叫作向量,也可以叫作矩阵。
OpenGL中矩阵声明:
//三维矩阵/四维矩阵的声明
typedef float M3DMatrix33f[9];
typedef float M3DMatrix44f[16];
值得一提的是,在其它很多编程语言中习惯使用二维数组来定义矩阵。但在OpenGL中,更偏向于使用一维数组来定义矩阵。 这样做的原因是:OpenGL 使⽤的是 Column-Major(以列为主)矩阵排序的约定。
矩阵分类
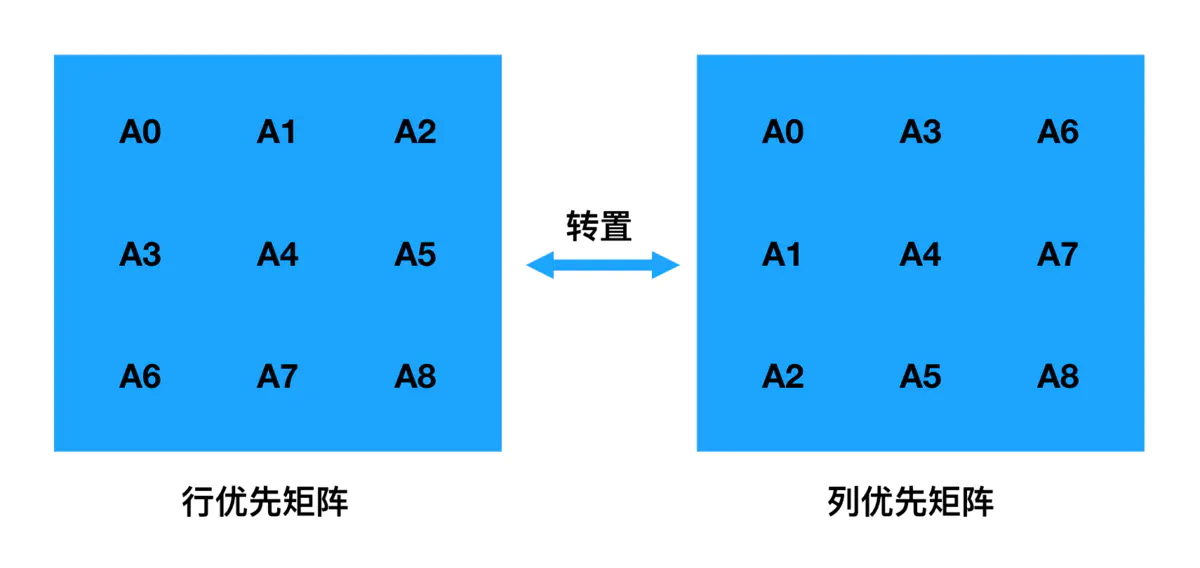
- 行优先矩阵:一行一行读取
- 列优先矩阵:一列一列读取
- 两者的关系为:行优先矩阵经过转置即可的到列优先矩阵
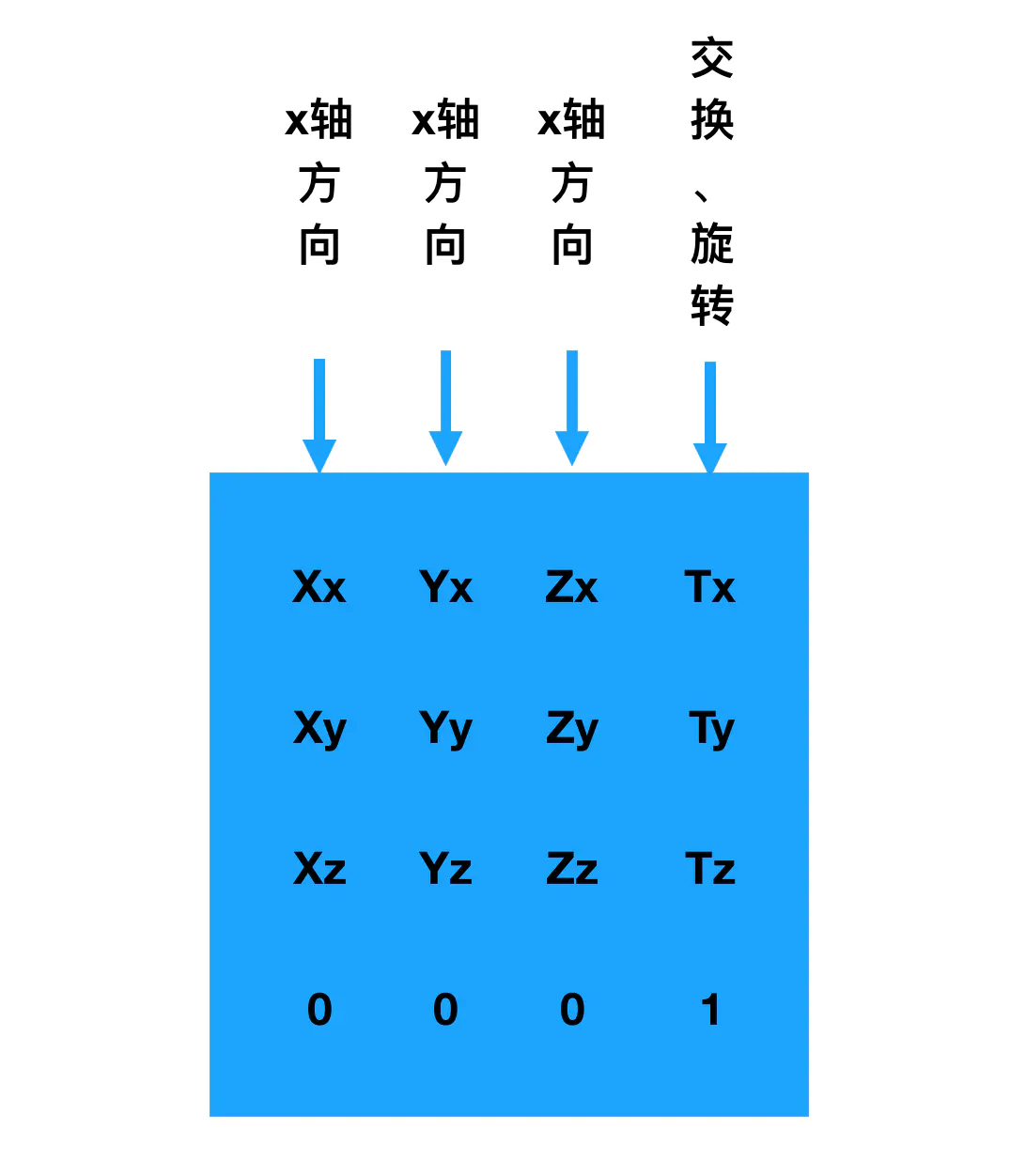
OpenGL矩阵奥秘之处在于这 16 个值表示空间中⼀个特定的位置; 这4列中,每⼀列都是有4个元素组成的向量;- 如果将⼀个对象所有的顶点向量 乘以这个矩阵,就能让整个对象变换到空间中给定的位置和⽅向;
- ⼀个4*4矩阵是如何在3D空间中表示⼀个位置和⽅向的列向量进⾏了特别的标注: 矩阵的最后⼀⾏都为0,只有最后⼀个元素为1。
单位矩阵
- 主对角线上数据都是1,其余元素都是0,即为单元矩阵 单元矩阵的初始化方式:
//单元矩阵初始化⽅式①
GLFloat m[] = {
1,0,0,0, //X Column
0,1,0,0, //Y Column
0,0,1,0, //Z Column
0,0,0,1 // Translation
}
// 单元矩阵初始化⽅式 ②
M3DMatrix44f m = {
1,0,0,0, //X Column
0,1,0,0, //Y Column
0,0,1,0, //Z Column
0,0,0,1 // Translation
}
//单元矩阵初始化⽅式③
void m3dLoadIdentity44f(M3DMatrix44f m);
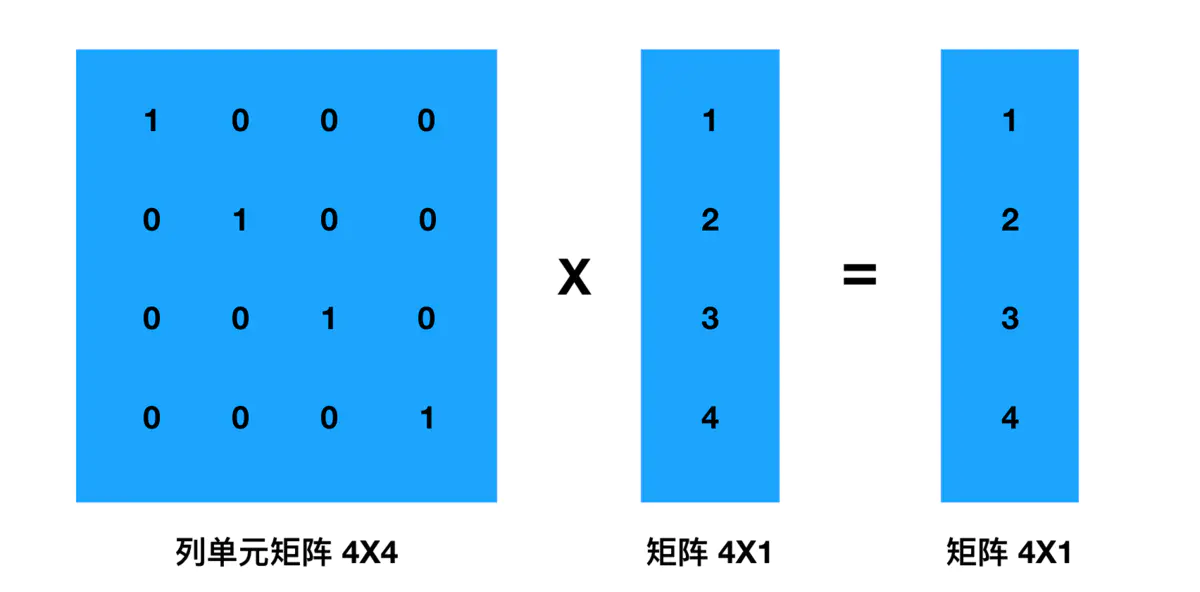
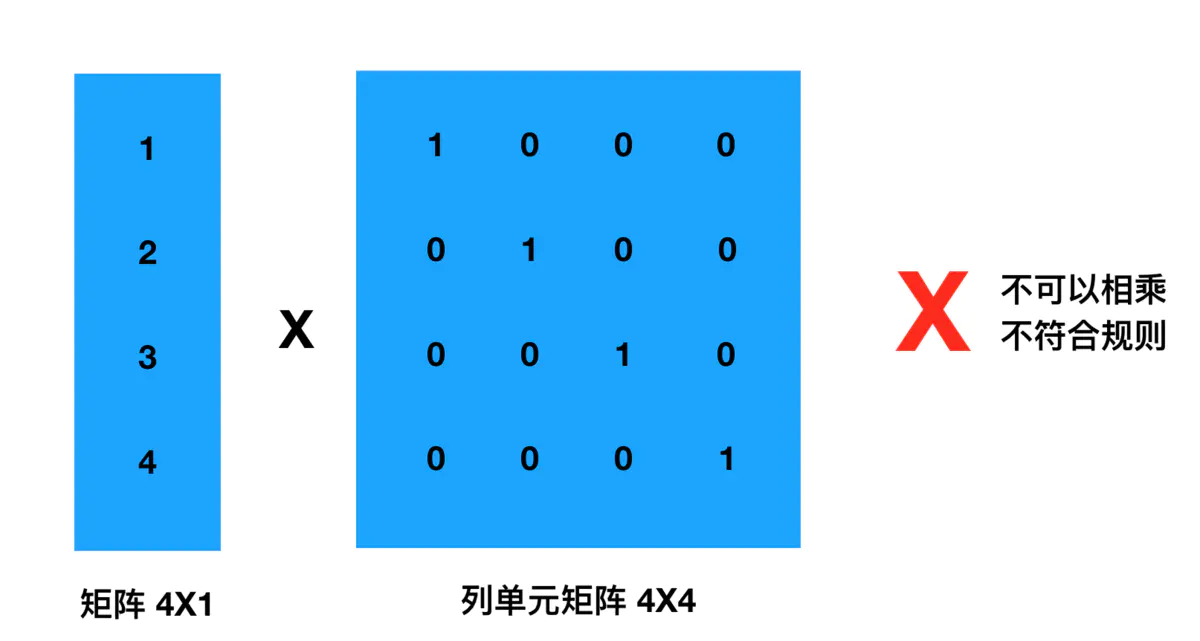
- 向量 X 单元矩阵 = 向量 X 1,不会发生任何变化
- 向量与单元矩阵相乘的前提是:向量的列数 == 单元矩阵的行数
理解OpenGL中的矩阵相乘
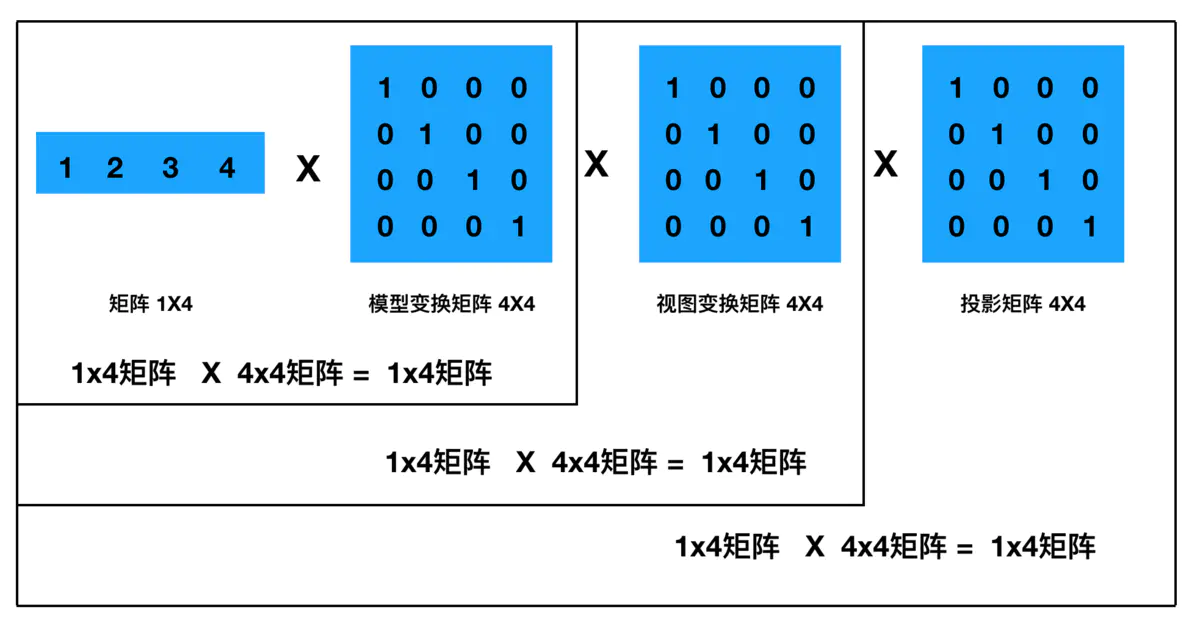
- 数学角度: 在线性代数数学的维度,为了便于书写. 所以坐标计算. 都是从左往右顺序,进⾏计算. 如下 列公式: 变换后顶点向量 =
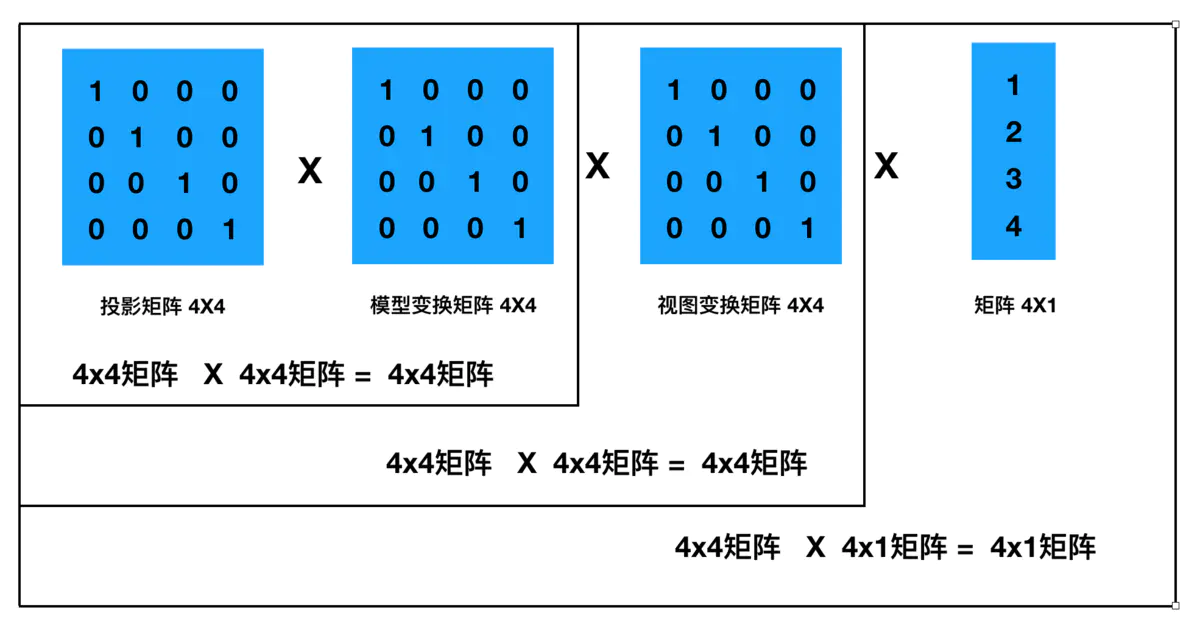
V_local * M_model * M_view * M_pro变换后顶点向量 = 顶点 ✖ 模型矩阵 ✖ 观察矩阵 ✖ 投影矩阵; 从数学角度理解mvp矩阵的计算,由于顶点是行向量,要满足矩阵相乘的规定条件(即 叉乘的前提),必须将mvp矩阵放在右边,属于右乘 OpenGL角度 在OpenGL 的维度. 如下列公式: 变换顶点向量 =M_pro * M_view * M_model * V_local变换顶点向量 = 投影矩阵 ✖ 视图变换矩阵 ✖ 模型矩阵 ✖ 顶点
OpenGL中的矩阵规定是以列为主,所以顶点以列向量的方式表示 从OpenGL角度理解mvp矩阵的计算,由于顶点是列向量,如果项进行矩阵规则,就需要满足矩阵相乘的条件,需要将mvp矩阵的顺序颠倒为pvm,且放在列向量的左边,属于左乘。
OpenGL中矩阵相乘源码:
inline void MultMatrix(const M3DMatrix44f mMatrix) {
//1. 从栈顶获取栈顶矩阵 复制到 mTemp
M3DMatrix44f mTemp;
// 2. 将栈顶矩阵 mTemp 左乘 mMatrix
m3dCopyMatrix44(mTemp, pStack[stackPointer]);
//3. 将结果放回栈顶空间⾥
m3dMatrixMultiply44(pStack[stackPointer], mTemp, mMatrix);
}
觉得不错记得点赞哦!听说看完点赞的人逢考必过,逢奖必中。ღ( ´・ᴗ・` )比心