42. 接雨水

解题思路

1. 暴力 时间 空间

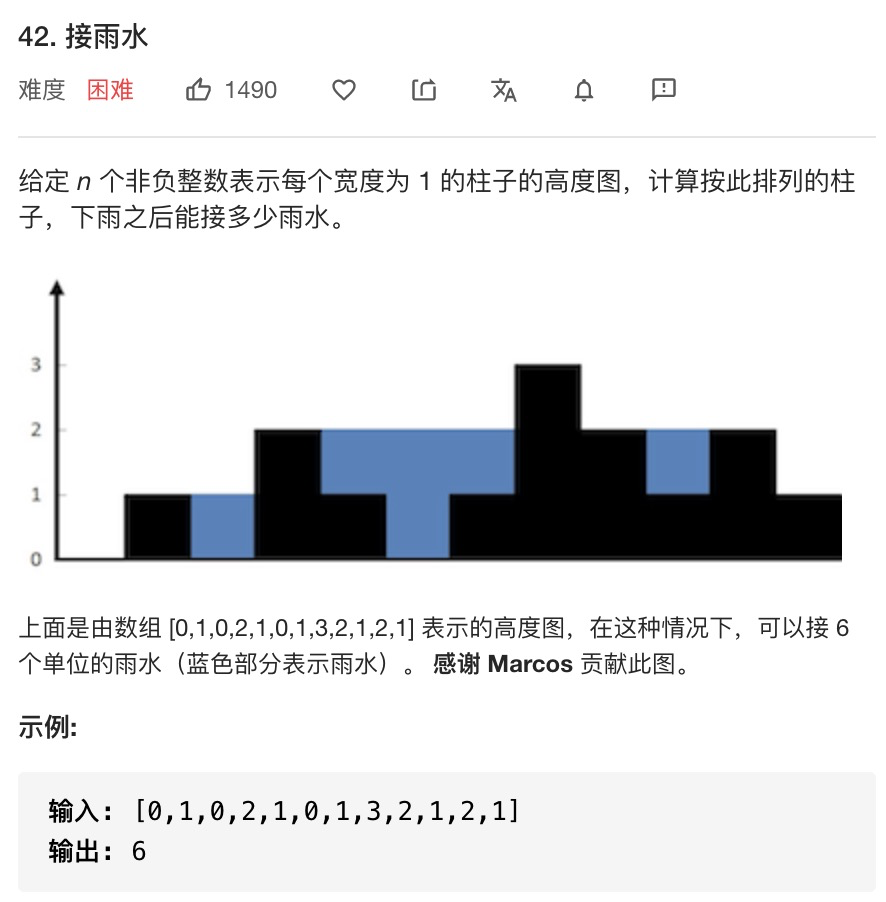
审题之后可以发现每个柱子顶部可以储水的高度，当前柱子的左右两侧最大高度的较小者减去当前柱子的高度。

因此我们只需要遍历每个柱子，累加每个柱子可以储水的高度即可。 参考代码1

class Solution {
    public int trap(int[] height) {
        if (height == null || height.length == 0) return 0;
        int res = 0;
        // 遍历每根柱子
 for (int i = 1; i < height.length - 1; i++) { int leftMax = 0, rightMax = 0; // 计算当前柱子中左侧柱子中最大高度 for (int j = 0; j <= i; j++) { leftMax = Math.max(leftMax, height[j]); } // 计算当前柱子中右子柱子中最大高度 for (int j = i; j < height.length; j++) { rightMax = Math.max(rightMax, height[j]); } // 结果中累加当前柱子顶部可以储水的高度 // 即 当前柱子左右两边最大高度的较小者 - 当前柱子的高度 res += Math.min(leftMax, rightMax) - height[i]; } return res; } } 

2.动态规划 时间 空间

通过上述暴力的方法，对于每个柱子，我们都需要从两头重新比那里一遍求出左右两侧的最大高度，这里很多重复计算的，很明显最大高度是可以记忆化的，具体在这里可以用数组边递推边存储，也就是常说的动态规划，DP。

具体做法：

1、 定义二维dp数组 int[][] dp = new int[n][2], 其中 dp[i][0] 表示下标i的柱子左边的最大值 , dp[i][1] 表示下标i的柱子右边的最大值。
2、 分别从两头遍历height数组，为 dp[i][0] 和 dp[i][1]赋值
3、 再遍历每个柱子，累加每个柱子可以储水的高度。 参考代码2

// 动态规划 时间O(n) 空间O(n)
    public int trap(int[] height) {
        int res = 0;
        if (height == null || height.length == 0) return res;
        int n = height.length;
 // 定义二维dp数组 // dp[i][0] 表示下标i的柱子左边的最大值 // dp[i][1] 表示下标i的柱子右边的最大值 int[][] dp = new int[n][2]; dp[0][0] = height[0]; dp[n-1][1] = height[n-1]; for(int i = 1; i < n; i++){ dp[i][0] = Math.max(height[i], dp[i-1][0]); } for(int i = n - 2; i >= 0; i--) { dp[i][1] = Math.max(height[i], dp[i+1][1]); } // 遍历每根柱子，累加当前柱子顶部可储水的高度 // 即，当前柱子的左右两边最大高度的较小者 - 当前柱子的高度 for(int i = 0; i < n; i++) { res += Math.min(dp[i][0], dp[i][1]) - height[i]; } return res; } 

3.双指针 时间 空间

在上述的动态规划方法中，我们利用二维数组来存储每个柱子左右两侧的最大高度，但我们递推累加每个柱子的储水高度时只用到来 do[i][0] 和 dp[i][1] 两个字，因此我们递推的时候只需要用 int leftMax 和 int rightMax 两个变量就行了。

即将上述代码中的递推公式：

res += Math.min(dp[i][0], dp[i][1]) - height[i];

优化成：

res += Math.min(leftMax, rightMax) - height[i];

注意这里的leftMax 是从左端开始递推得到的，而 rightMax 是从右端开始递推得到的。

因此遍历每个柱子，累加每个柱子的储水高度时，也需要用 left 和 right 两个指针从两端开始遍历。

参考代码3

// 双指针 时间O(n) 空间O(1)
    public int trap(int[] height) {
        int res = 0;
        if (height == null || height.length == 0) return res;
        // 定义两个指针
 int left = 0, right = height.length - 1, leftMax = 0, rightMax = 0; while (left <= right) { // 左端最高柱子小于右端最好柱子 if (leftMax <= rightMax) { // 与当前柱子比较去较大的 leftMax = Math.max(leftMax, height[left]); res += leftMax - height[left++]; } else { rightMax = Math.max(rightMax, height[right]); res += rightMax - height[right--]; } } return res; } 

4. 单调栈 时间 空间

单调栈是本文想重要说明的一个方法～

因为本题是一道典型的单调栈的应用题

简单来说就是当前柱子如果小于等于栈顶元素，说明形不成凹槽，则将当前柱子入栈； 反之若当前柱子大于栈顶元素，说明形成了凹槽，于是将栈中小于当前柱子的元素pop出来，将凹槽的大小累加到结果中。

关于凹槽的理解，我们可以先看一下gif图： 通过上图哭发现，遍历到某些柱子的时候，会由于和之前的某个柱子形成凹槽，接住雨水。

这道题目可以用单调栈来做。单调栈就是比普通的栈多一个性质，即维护栈内元素单调。

比如当前某个单调递减额栈的元素从栈底到栈顶分别是：[10,9,8,3,4]，如果要入栈元素 5，需要把栈顶元素pop出去，直到满足单调递减为止，即先变成[10,9,8]，再入栈5，就是[10,9,8,5]。

演示：

我们为这道题演示一下[4, 3, 1, 0, 1, 2, 4]是怎么接雨水的，下图是最终的接雨水效果，蓝色部分是雨水。

接下来我们开始演示，下面的图示中，最上方是每个柱子的高度。左侧是单调栈的元素。图中有红色边框的柱子是存在于单调栈里的元素。

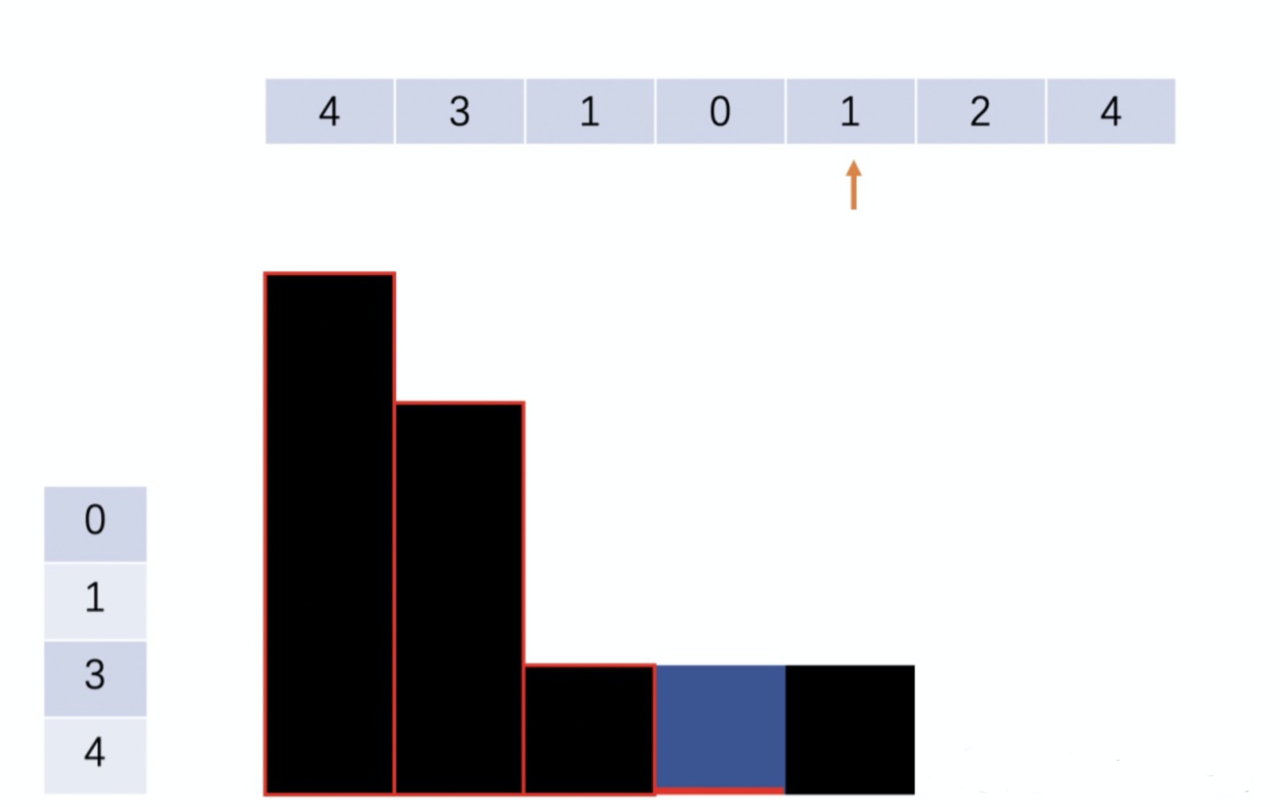
Step 1: 遍历到下图中箭头所指向的位置时，栈内元素是[4, 3, 1, 0]。由于当前柱体的高度为1大于栈顶元素0，那就可以接住雨水。接住雨水的量的高度是栈顶元素和左右两边形成的高度差的min。宽度是1。

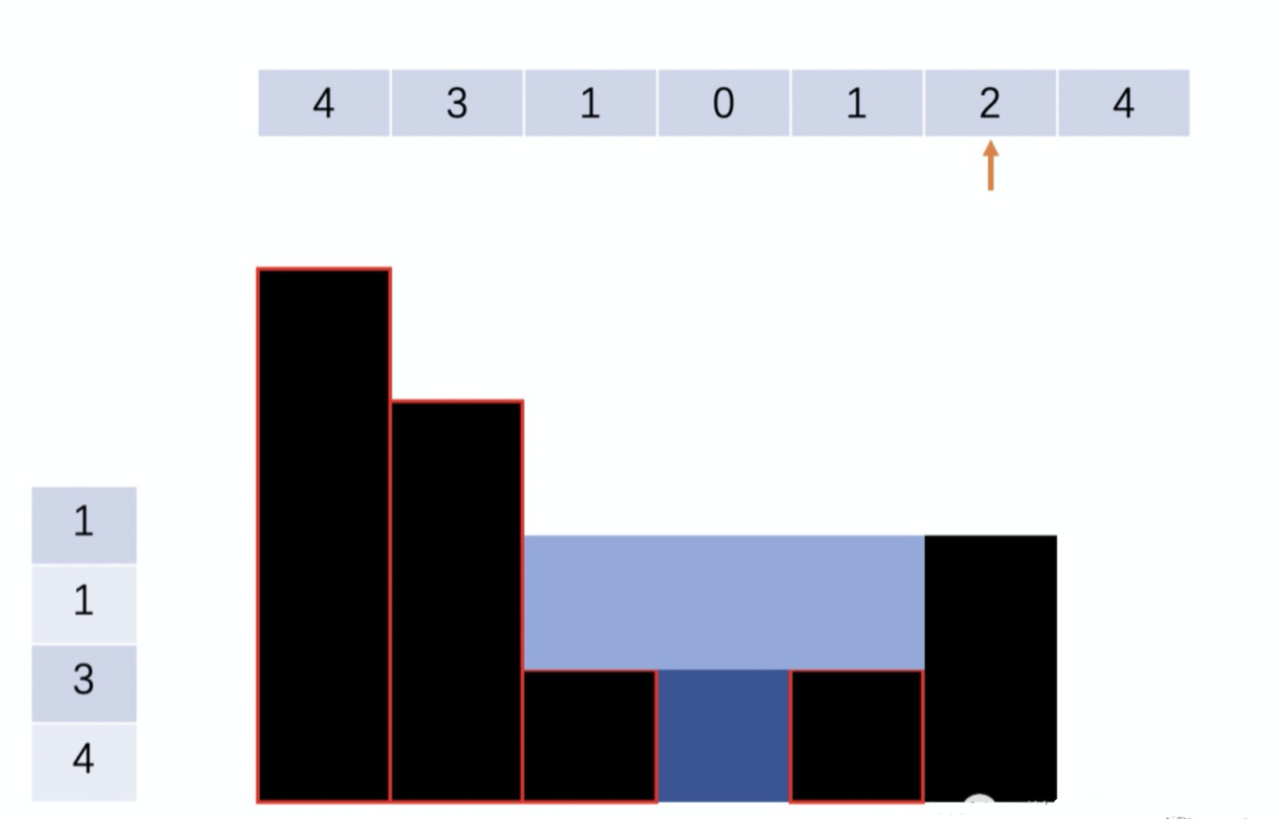
Step 2: 遍历到下图中箭头所指向的位置时，栈内元素是[4, 3, 1, 1]。由于当前的柱体的高度为2大于栈顶元素1，那就可以接住雨水。由于栈顶元素有相等的情况，所以可以把1全都pop出去，变成[4, 3]。此时形成的新凹槽的高度是此时的栈顶元素3和当前高度为2的柱体的高度的min再减去先前的栈顶元素1，新凹槽的宽度是此时栈顶元素的位置和当前高度为2的柱体的位置的距离。可以算出来此次接住的雨水是1 * 3。

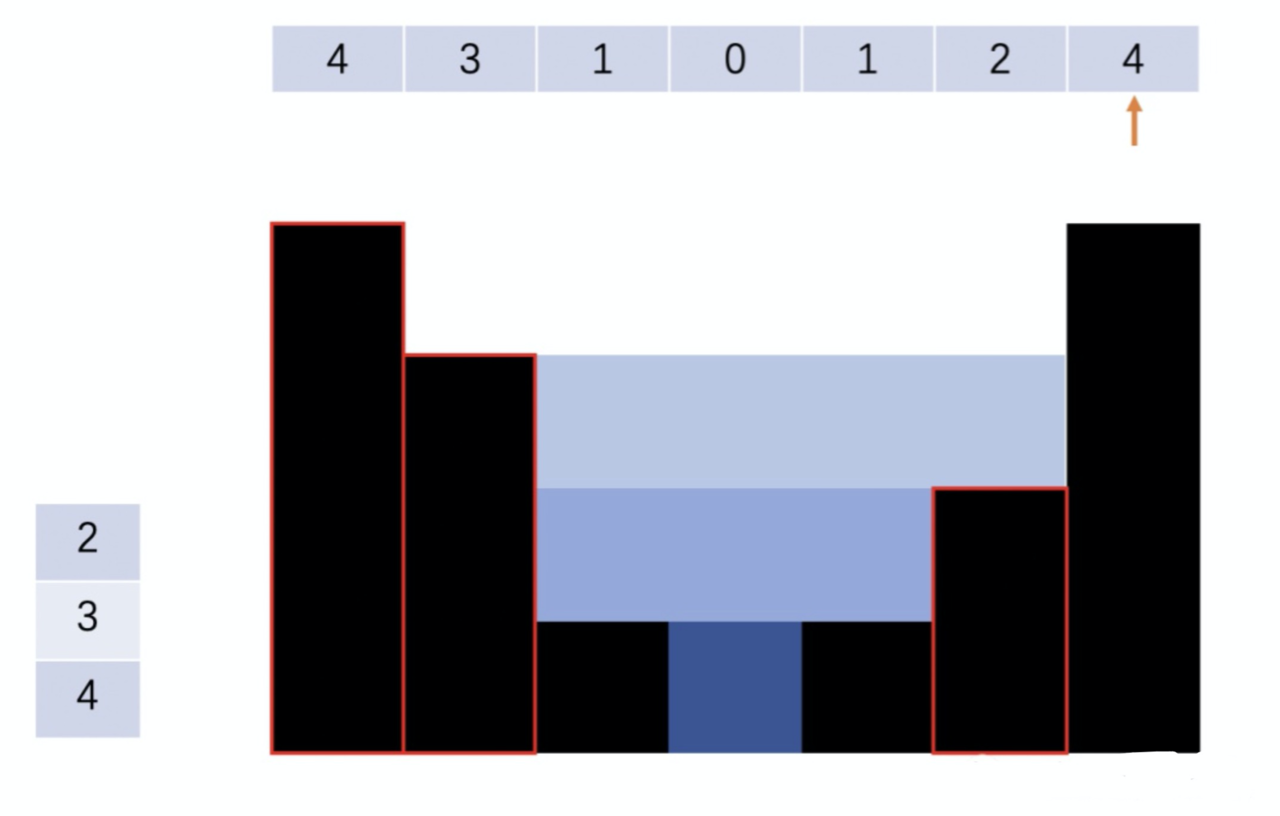
Step 3: 遍历到下图中箭头所指向的位置时，栈内元素是 [4, 3, 2]。由于当前的柱体的高度为4大于栈顶元素2，把 2 pop出来，栈顶元素3所在位置和当前高为4的柱体可以接住雨水，雨水量是 1 * 4。

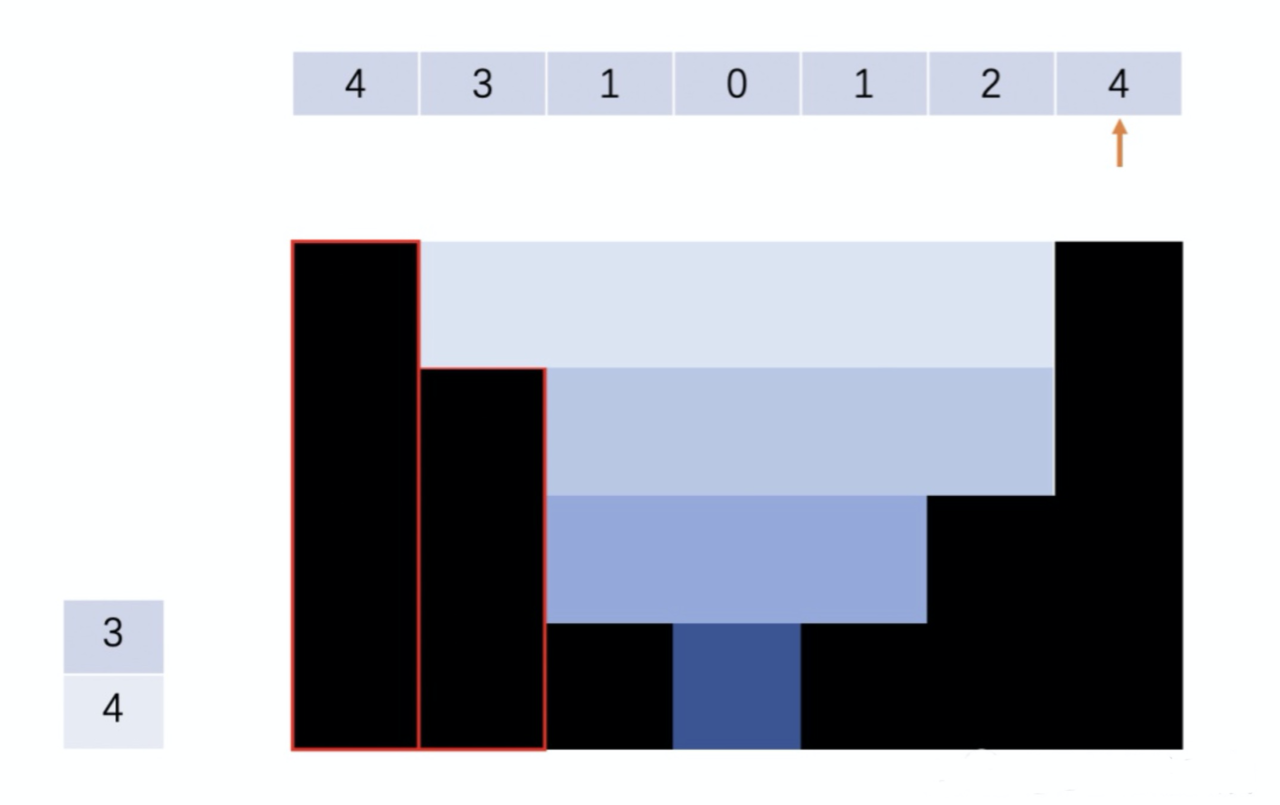
Step 4: 由于上步的栈顶元素3仍然小于当前的柱体高度4，因此pop出3。新栈顶元素4所在位置和当前高为4的柱体可以接住雨水，雨水量是 1 * 5。

这样每个部分的雨水量都可以算出来，加在一起就可以了。由于每个柱体最多入栈出栈一次，所以时间复杂度 O(N)。

代码就很简单了，具体见注释～

参考代码4

// 单调栈 时间O(n) 空间O(n)
class Solution {
    public int trap(int[] height) {
        Stack<Integer> stack = new Stack<>();
        int res = 0;
 // 遍历每个柱体 for (int i = 0; i < height.length; i++) { while (!stack.isEmpty() && height[stack.peek()] < height[i]) { int bottomIdx = stack.pop(); // 如果栈顶元素一直相等，那么全都pop出去，只留第一个。 while (!stack.isEmpty() && height[stack.peek()] == height[bottomIdx]) { stack.pop(); } if (!stack.isEmpty()) { // stack.peek()是此次接住的雨水的左边界的位置，右边界是当前的柱体，即i。 // Math.min(height[stack.peek()], height[i]) 是左右柱子高度的min，减去height[bottomIdx]就是雨水的高度。 // i - stack.peek() - 1 是雨水的宽度。 res += (Math.min(height[stack.peek()], height[i]) - height[bottomIdx]) * (i - stack.peek() - 1); } } stack.push(i); } return res; } } 

最后，为了加强对单调栈的理解，还可以去做一下：84. 柱状图中最大的矩形

文章参考：甜姨的力扣题解

部分图片来源于网络，版权归原作者，侵删。

文章永久链接：https://tech.souyunku.com/33849