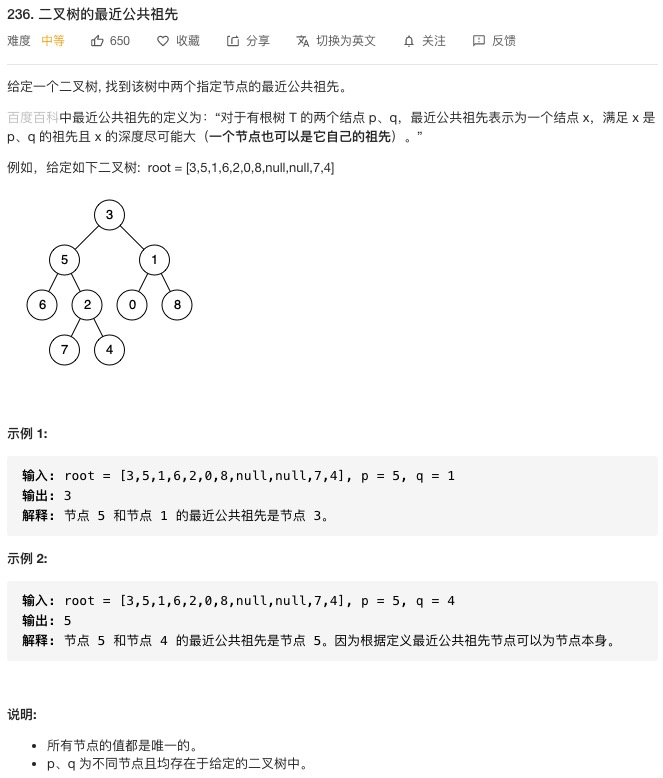
236. 二叉树的最近公共祖先

解题思路

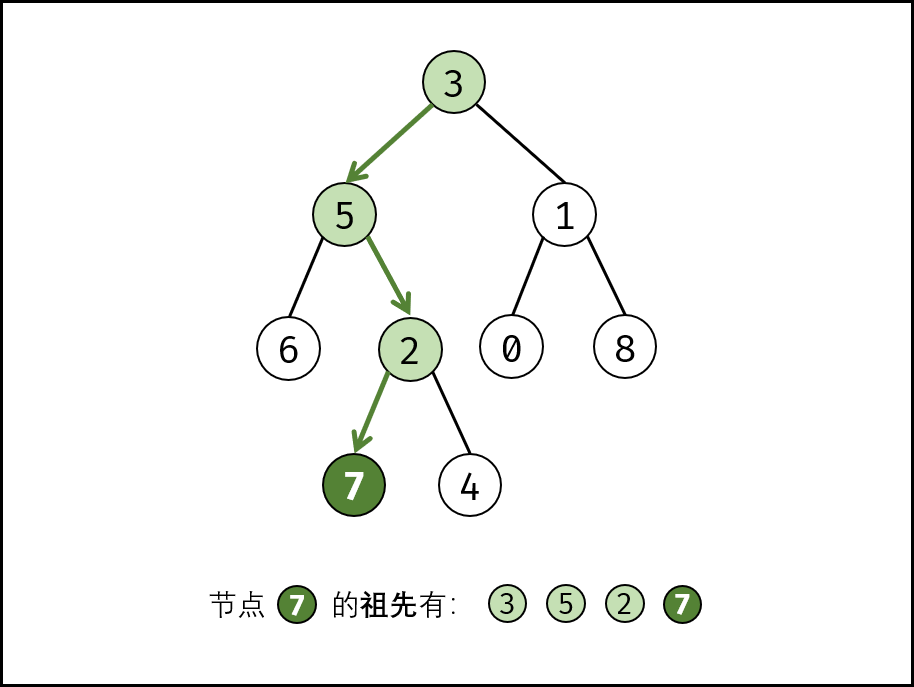
祖先的定义： 若节点 在节点 的左(右)子树中，或 ，则称 是 的祖先。

最近公共祖先的定义： 设节点 为 节点 的某公共祖先，若其左子节点 和 右子节点 都不是 的公共祖先，则称 是 “最近的公共祖先”。

根据以上定义，若 是 的最近公共祖先，则只可能为以下情况之一：

1、 和 在 的子树中，且分列 的 异侧（即分别在左、右子树中）；
2、 ，且 在 的左或右子树中；
3、 ，且 在 的左或右子树中；

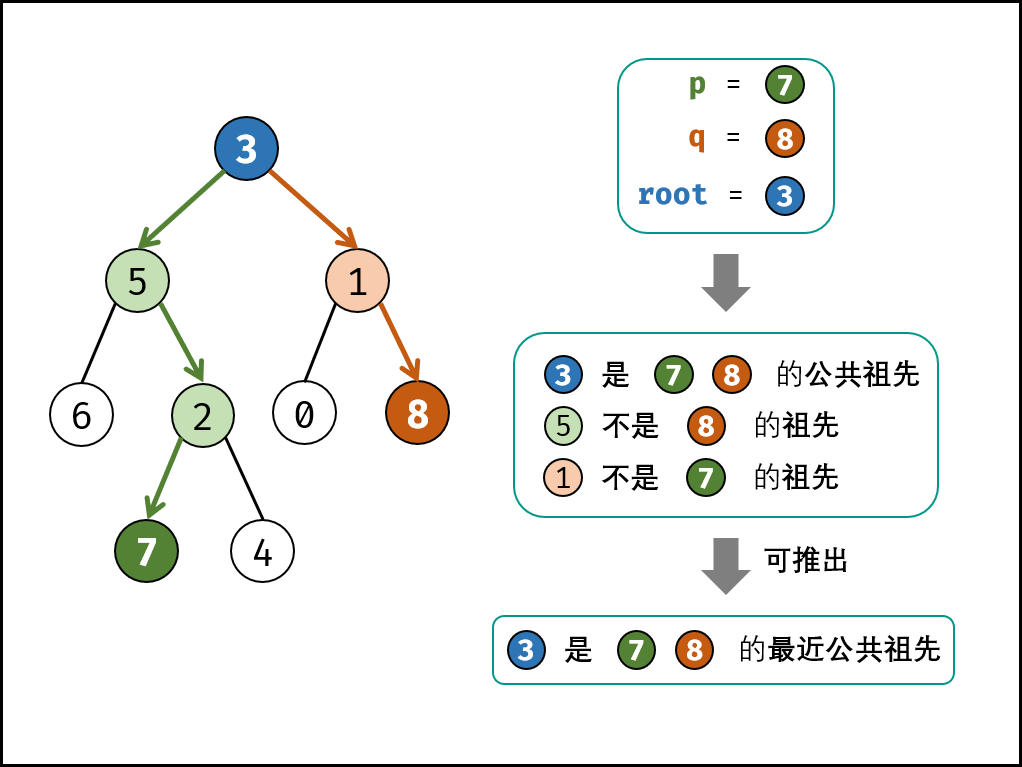
考虑通过递归对二叉树进行后序遍历，当遇到节点 p 或 q 时返回。从底至顶回溯，当节点 p、q 在节点 root 的异侧时，节点 root 即为最近公共祖先，则向上返回 root。

递归解析

1、 终止条件

• 当越过叶节点，则直接返回 ；
• 当 等于 ，则直接返回 ；

1、 递归工作

• 开启递归左子节点，返回值记为 ；
• 开启递归右子节点，返回值记为 ；

1、 返回值：根据 和 ，可展开为四种情况：

• 当 和 同时为空：说明 的左/右子树都不包含 ，返回 ；
• 当 和 同时不为空：说明 分列在 的 异侧（分别在左/右子树），因此 为最近公共祖先，返回 。
• 当 为空， 不为空： 都不在 的左子树中，直接返回 。具体可以分为两种情况：
  • （1） 其中一个在 的 右子树中，此时 指向 p (假设为 )
  • （2） 两节点都在 的 右子树中，此时的 指向 最近公共祖先节点

1、 当 不为空， 为空：于情况 3 同理。

观察发现，情况1 可合并至 3 和 4 内。

参考代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 * TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { if (root == null || root == p || root == q) return root; TreeNode left = lowestCommonAncestor(root.left, p, q); TreeNode right = lowestCommonAncestor(root.right, p, q); if(left == null) return right; if(right == null) return left; return root; } public TreeNode lowestCommonAncestor2(TreeNode root, TreeNode p, TreeNode q) { if(root == null || root == p || root == q) return root; TreeNode left = lowestCommonAncestor(root.left, p, q); TreeNode right = lowestCommonAncestor(root.right, p, q); if(left == null && right == null) return null; //1. if(left == null) return right; // 3. if(right == null) return left; // 4. return root; //2. if(left != null && right != null) } } 

部分图片来源于网络，版权归原作者，侵删。

文章永久链接：https://tech.souyunku.com/33857