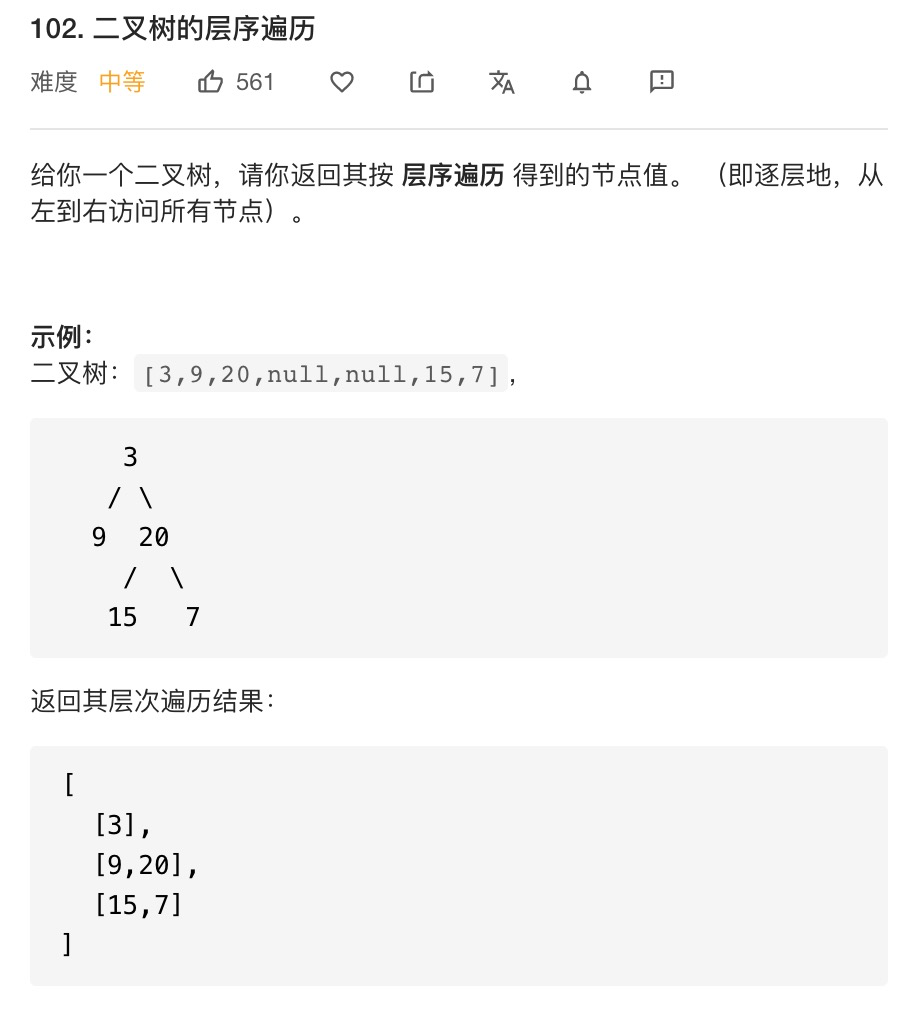
102. 二叉树的层序遍历
解题思路
DFS 与 BFS
让我们先看看在二叉树上进行DFS遍历和BFS遍历的代码比较。
DFS 遍历使用递归:
void dfs(TreeNode root) {
if (root == null) {
return;
}
dfs(root.left);
dfs(root.right); }
BSF 遍历使用队列数据结构:
void bfs(TreeNode root) {
Queue<TreeNode> queue = new ArrayQueue<>();
queue.add(root);
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
if (cur.left != null) { queue.add(cur.left); } if (cur.right != null) { queue.add(cur.right); } } }
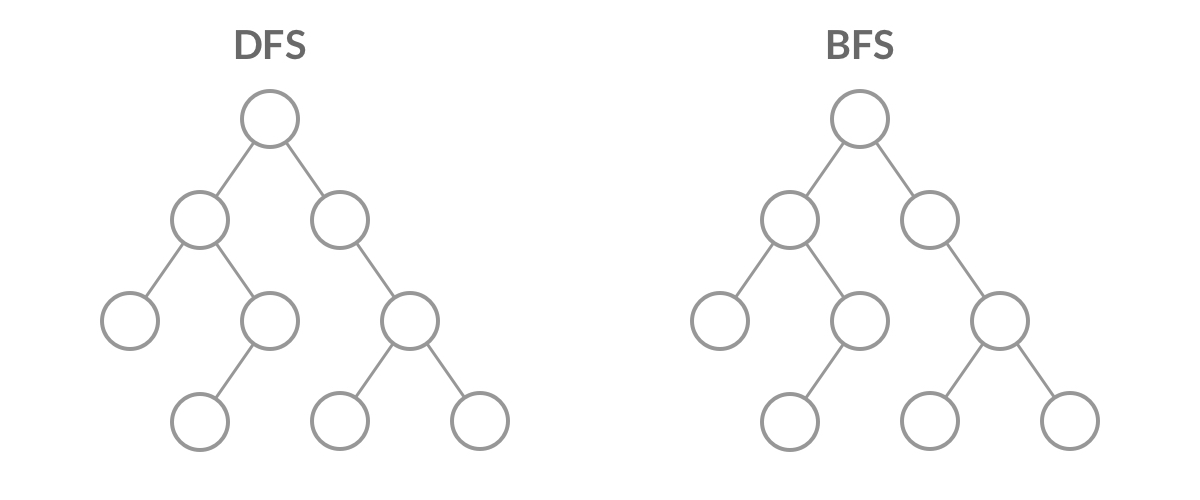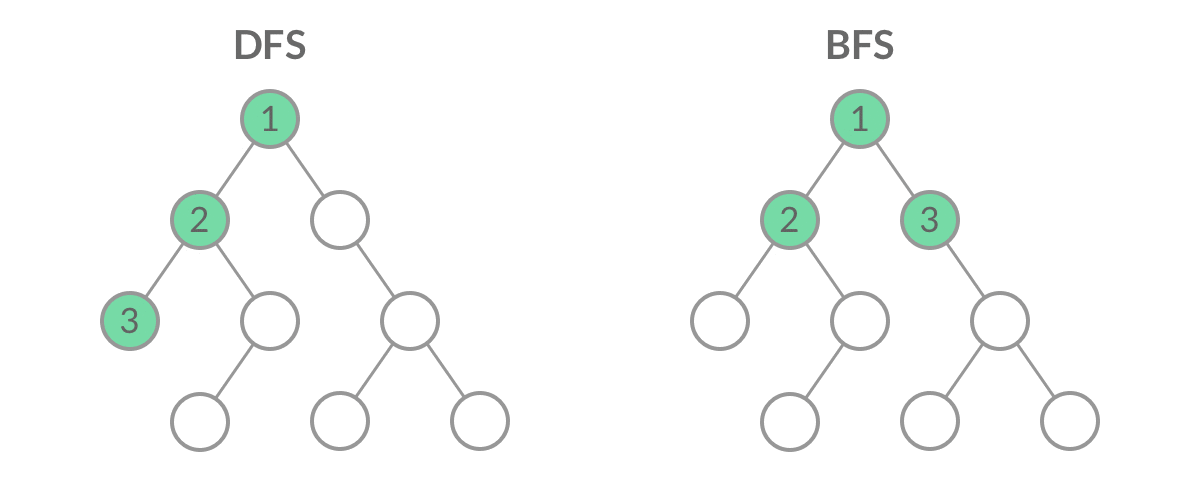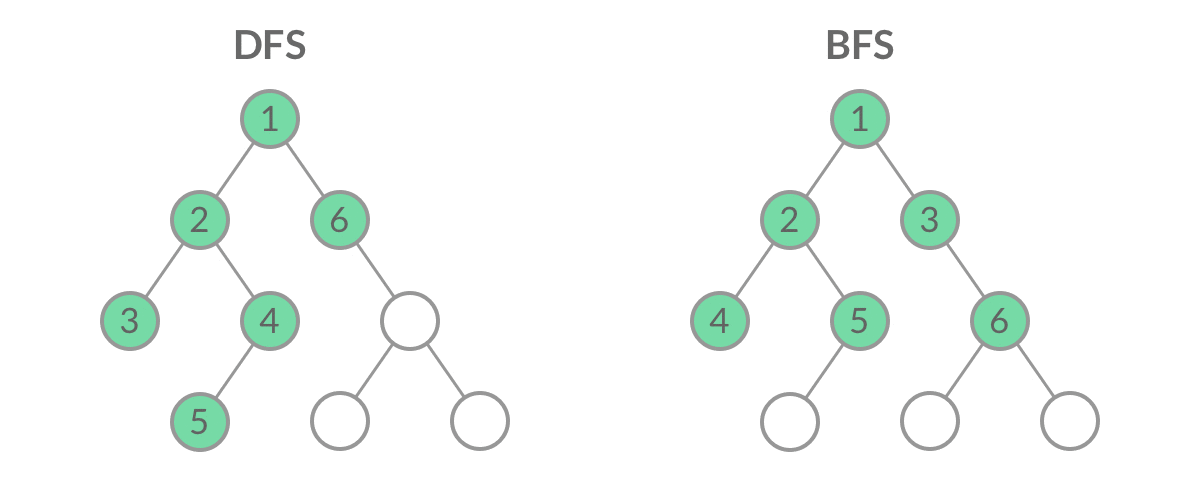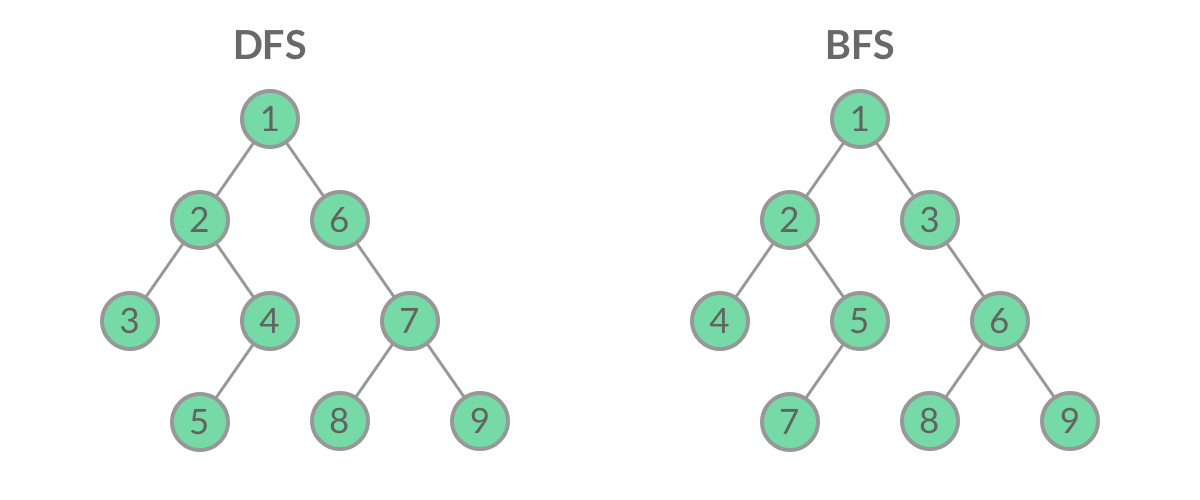
DFS 遍历的代码比 BFS 简洁很多,这是因为递归的方式隐含地使用了系统的 栈 ,不需要直接维护一个数据结构。 虽然 DFS 和 BFS 都是将二叉树的所有结点遍历了一遍,但它们的遍历结点的顺序不同。
DFS 递归的方式
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { public List<List<Integer>> levelOrder(TreeNode root) { List<List<Integer>> list = new ArrayList<>(); if (root == null) return list; dfs(root,1, list); return list; } private void dfs(TreeNode root, int level, List<List<Integer>> list) { // 当前集合小于树深度(层级) if(list.size() < level) { // 添加个空集合到返回结果中 list.add(new ArrayList()); } // 通过下标减1获取空集合并添加树结点值 list.get(level - 1).add(root.val); // 判断左右子树,进入下一层,树深度加1 if (root.left != null) { dfs(root.left, level + 1, list); } if (root.right != null) { dfs(root.right, level + 1, list); } } }
BFS 迭代方式
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right; * TreeNode(int x) { val = x; } * } */ class Solution { public List<List<Integer>> levelOrder(TreeNode root) { List<List<Integer>> list = new ArrayList<>(); if (root == null) return list; Deque<TreeNode> deq = new ArrayDeque<>(); deq.add(root); while (!deq.isEmpty()) { int n = deq.size(); List<Integer> level = new ArrayList<>(); for (int i = 0; i < n; i++) { // 变量 i 无实际意义,只是为了循环 n 次 TreeNode cur = deq.poll(); level.add(cur.val); if (cur.left != null) deq.add(cur.left); if (cur.right != null) deq.add(cur.right); } list.add(level); } return list; } }
部分图片来源于网络,版权归原作者,侵删。