无向图最小生成树问题描述
一个无向图G的最小生成树就是由该图的那些链接G的所有顶点的边构成的树,其总价值最低。 最小生成树存在当且仅当图是连通的。为了简便考虑, 下面的算法都是假设图是连通的。 无向图最小生成树有两个典型的算法Prim和Kruskal,下面分别介绍。
Prim算法
算法核心思想
以贪婪策略,一步一步将关联顶点增加到树上。
算法介绍
算法的每一阶段都是通过:
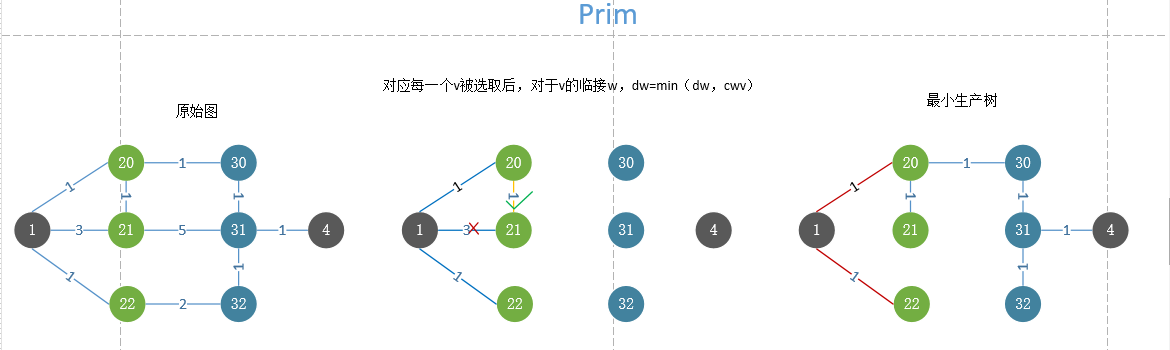
1、 选择一条边(u,v)使得(u,v)的值是所有u在树上但v不在树上的边的值中的最小者。并把相应的顶点v添加到这颗树上。
2、 继续上述步骤,直到所有顶点都在树上。
图解示例
核心代码
public void prim(Vertex start){
//初始声明所有顶点均不在树上
for(Vertex v:graph){
v.isInTree=false;
v.dist=Integer.MAX_VALUE;
}
start.dist = 0;// 声明起点的距离为0
//以顶点的最短距离构建堆
PriorityQueue<Vertex> priorityQueue = new PriorityQueue<Vertex>();
priorityQueue.add(start);
while(!priorityQueue.isEmpty()){
Vertex v=priorityQueue.poll();
if(v!=null){
if(!v.isInTree){//取出的顶点不在树上
//1. 声明顶点在树上
v.isInTree=true;
if(v.adj!=null&&!v.adj.isEmpty()){
for(AdjVertex adjw:v.adj){
//更新临接表中 最短距离有变化的顶点,并将该顶点加入到优先队列
if(adjw.cvw<adjw.w.dist){
adjw.w.setDist(adjw.cvw);
adjw.w.setPath(v);
priorityQueue.add(adjw.w);
}
}
}
}
}
}
}
Kruskal算法
算法核心思想
以贪婪策略,连续按照最小的权选择备选边,并且当所选的边不会产生圈时选定该边。
算法介绍
分析
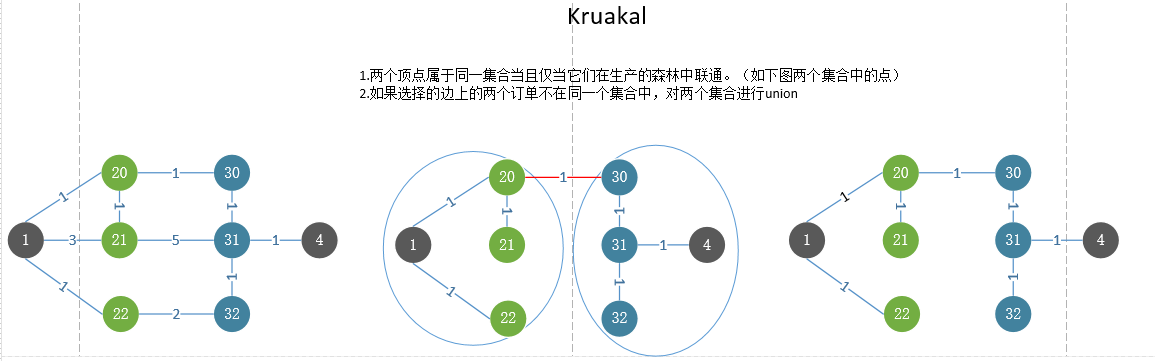
Kruskal类似处理一个森林。初始时,有存在|V|颗单节点树,每添加一条边即将两棵树合并,当算法终止时就只有一颗树。
数据结构选择
1、 经过上述分析,Kruskal所需要的数据结构需要很好的支持find(即找到节点所属的当前树)和union操作(即合并两颗树)。目前良好的支持find/union操作的数据结构就是不相交集合。
2、 每次选择最小权的边。以边的权构建堆,每次执行deletemin操作。
算法核心
在算法的任意时刻,两个顶点属于同一个集合当且仅当它们在当前的生成森林中连通。
图解示例
核心代码
public List<Edge> kruskal() {
List<Edge> result = new ArrayList<Edge>();
int vertexSize = graph.values().size();
int acceptedEdge = 0;
//以点的数量构建不相交集合
DisjSets disjSets = new DisjSets(vertexSize);
//以边的权构建堆
PriorityQueue<Edge> priorityQueue = new PriorityQueue<Edge>(getEdges());
while (acceptedEdge < vertexSize - 1&&!priorityQueue.isEmpty()) {
Edge e = priorityQueue.poll();
int disv = disjSets.find(e.vnum);
int disw = disjSets.find(e.wnum);
if (disv != disw) {
//两个顶点不在一颗树上,合并两个顶点
acceptedEdge++;
disjSets.union(disv, disw);
result.add(e);
}
}
return result;
}
完整代码地址
github
Prim
码云