前言
大家好,感谢大家对前两篇博客的支持。今天我准备提供归并,快排,快速选择的笔记,这三个是分治算法的典型例子。这次有利用叠缩证明算法的时间界限哦!,另外代码已经放到码云上啦。
分治算法
分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题,这些子问题相互独立且与原问题性质相同。求出子问题的解,就可得到原问题的解。即一种分目标完成程序算法,简单问题可用二分法完成。
归并,快排,快速选择是分治思想的三个典型例子。
Java中对应的算法
一般排序使用Java提供的归并算法,即Collections.sort(..)。快速选择一般用于解决TopN问题, 下面分别介绍三个算法。
1归并排序
简介
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法。
算法介绍
该算法的基本操作是合并两个已排序的表,下面举例说明合并过程:
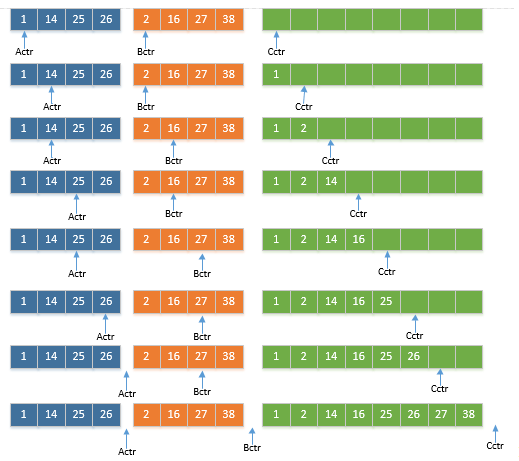
算法描述详细描述:
- 如果N=1,只有一个元素,直接返回
- 否则,前半部分和后半部分各自进行归并排序,得到排序过的两部分,之后按照上面的算法进行合并。
核心代码示例
private static <AnyType extends Comparable<? super AnyType>>
void mergeSort(AnyType[] a, AnyType[] tmpArray,
int left, int right) {
if (left < right) {
int center = (left + right) / 2;
// 如下方式排除了只有3个元素的情况,只有三个元素是 center=1
mergeSort(a, tmpArray, left, center);
mergeSort(a, tmpArray, center + 1, right);
merge(a, tmpArray, left, center + 1, right);
}
}
/**
* 合并函数,归并排序的基本步骤
* @param a 原始数据数组
* @param tmpArray 归并使用的第三个临时数组
* @param leftPos 左边部分开始,对应图上Actr初始位置
* @param rightPos 右边开始 ,对应Bctr初始位置
* @param rightEnd 右边结束 ,对应Bctr结束位置
*/
private static <AnyType extends Comparable<? super AnyType>>
void merge(AnyType[] a, AnyType[] tmpArray,
int leftPos, int rightPos, int rightEnd) {
// 一定范围内合并
//左边结束,对应图上Actr结束位置
int leftEnd = rightPos - 1;
int tmpPos = leftPos;
//本次合并总共包含的元素数量
int numElements = rightEnd - leftPos + 1;
//进行归并
while (leftPos <= leftEnd && rightPos <= rightEnd) {
if (a[leftPos].compareTo(a[rightPos]) <= 0) {
tmpArray[tmpPos++] = a[leftPos++];
} else {
tmpArray[tmpPos++] = a[rightPos++];
}
}
while (leftPos <= leftEnd) {
tmpArray[tmpPos++] = a[leftPos++];
}
while (rightPos <= rightEnd) {
tmpArray[tmpPos++] = a[rightPos++];
}
// 将排序过的数据拷贝会原始数组,【只有rightEnd没有变化】。
for (int i = 0; i < numElements; i++, rightEnd--) {
a[rightEnd] = tmpArray[rightEnd];
}
}
分析
根据前面的描述可以得出如下通项公式:
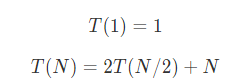
使用叠缩求和,进行推导,两边除以N
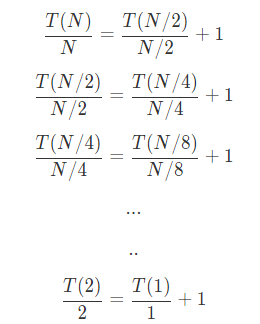
之后进行求和两边减去公项后结果为:
之后两边同乘以N,得到时间界:
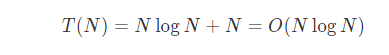
2快速排序
简介
快速排序(Quicksort) 的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列
算法介绍
- 简单4步
1、 如果S中元素个数为0或1,则返回,或者S中元素小于CUTOFF,则将S排序
2、 以三数中值取枢元v
3、 将S-{v}划分为两个不相交集合,并确定枢元v的位置:
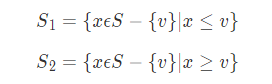
4、 按如下顺序分治其余部分处理
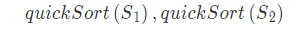
- 举例说明
-
- 三数中值取枢元
即左端,右端和中心的中值作为枢元,(实际能够减少14%的比较次数). 将最小值放到左端, 最大值放到右端, 中值放到次右端, 原中值处放次右端值。
三数中值取枢元
- 三数中值取枢元
-
- 分割示意
分割示意
- 分割示意
核心代码示意
/**
* 三数中值分割法
* @param a 原始数组
* @param left 左边界
* @param right 右边界
* @return 返回枢元
*/
private static <AnyType extends Comparable<? super AnyType>>
AnyType median3(AnyType[] a, int left, int right) {
int center=(left+right)/2;
if(a[center].compareTo(a[left])<0){
swapReferences(a, left, center);
}
if(a[right].compareTo(a[left])<0){
swapReferences(a, left, right);
}
if(a[right].compareTo(a[center])<0){
swapReferences(a, center, right);
}
swapReferences(a, center, right-1);
return a[right-1];
}
/**
* 快排核心
* @param a 原始数组
* @param left 左边界
* @param right 右边界
*/
private static <AnyType extends Comparable<? super AnyType>>
void quickSort(AnyType[] a, int left, int right) {
if(left+CUTOFF<=right){
//三数中值分割法,取枢元
AnyType pivot=median3(a,left,right);
int i=left;
int j=right-1;
while(true){
//i找大于枢元的元素
while(a[++i].compareTo(pivot)<0);
//j找小于枢元的元素
while(a[--j].compareTo(pivot)>0);
if(i<j){
swapReferences(a, i, j);
}else{//i>j,此轮分割结束
break;
}
}
//交换i,与枢元
swapReferences(a, i, right-1);
//分治进行,快排
quickSort(a,0,i-1);
quickSort(a,i+1,right);
}else{
insertSort(a, left, right);
}
}
时间复杂度
- 最坏情况
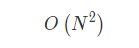
- 平均情况和最好情况
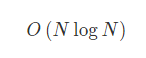
- 平均情况分析
假设S1,每个大小都是等可能的。
由于该假设,可知
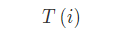
和
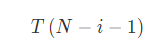
的平均值为
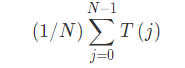
可以得到通项为:
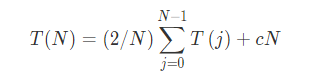
两边乘以N得到式子1如下:
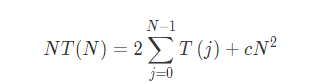
由N通项得出N-1通项如下为式子2:
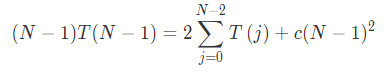
式子1-式子2,得到如下:
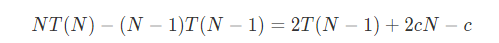
除去无关系-c,进行叠缩:
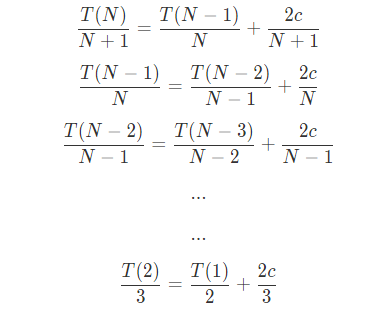
进行求和:
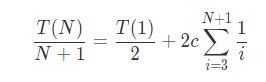
该和大概为O(logN),于是得到平均时间界限:
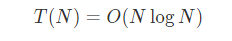
3快速选择
问题描述
乱序集合中找到第K个最小元。
算法介绍
依照快排思路进行处理:
1、 如果S=1,K=1将S中元素直接返回,若
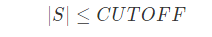
则将S排序返回第k个最小元。 2. 以三数中值取枢元v 3. 将S-{v}划分为两个不相交集合,并确定枢元v的位置:
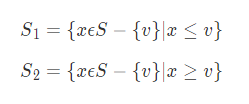
4、 如果 
第K个元素在
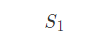
中,返回

否则返回:

代码
/**
* 快速选择核心
* @param a 原始数组
* @param left 左边界
* @param right 右边界
* @param k 需要选择的位
*/
private static<AnyType extends Comparable<? super AnyType>> void
quickSelect(AnyType[] a, int left, int right, int k) {
if(left+CUTOFF<=right){
AnyType pivot=median3(a, left, right);
int i=left;
int j=right-1;
while(true){
while(a[++i].compareTo(pivot)<0);
while(a[--j].compareTo(pivot)>0);
if(i<j){
swapReferences(a, i, j);
}else{
break;
}
}
swapReferences(a, i, right-1);
if(k<=i){
quickSelect(a, left, i-1, k);
}else if(k>i+1){
quickSelect(a, i+1, right, k);
}
}else{
insertSort(a, left, right);
}
}
总结
1、 快排和归并排序算法的平均时间界限是NlogN,Java默认使用归并算法。
2、 快速选择是TopN算法的经典解法,但是本人工程中用到较少
完整代码地址:
码云: 归并&快排: 点击查看 快速选择 : 点击查看
github: 归并&快排 快速选择
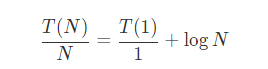
 三数中值取枢元
三数中值取枢元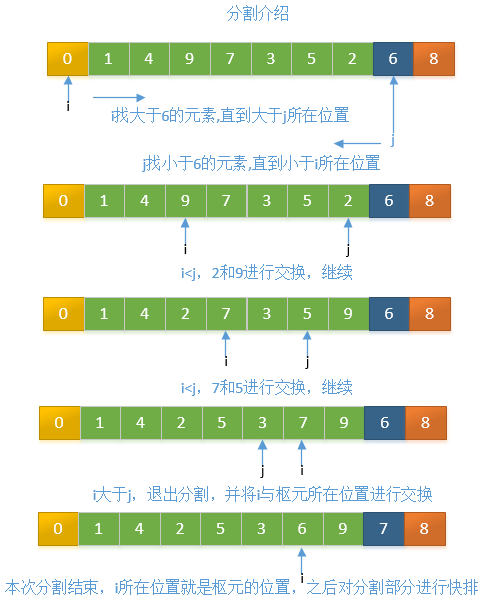 分割示意
分割示意