前言
大家好，今天提供不相交集合的笔记（即union/find）. 不相交集合有实现简单，证明困难的特点，若有想证明的可以自行查阅相关文献。我就不做赘述啦！
用途
不相交集类解决动态等价类问题，即：
1、 查找find一个元素属于哪个等价类，
2、 合并union 两个等价类为一个新的等价类。
也就是常说的union/find算法
基本概念介绍
等价类定义
1、 一个元素a属于S的等价类是S的一个子集合，它包含所有与a有等价关系的元素。
2、 等价类对S进行划分：S中的每一个成员恰好出现在一个等级类中。
等价关系定义
1、 自反性 a属于S，aRa (R代表关系)
2、 对称性 aRb，bRa
3、 传递性 aRb,bRc则 aRc
举例
1、 “>”号不是等价关系，没有对称性
2、 电器连通性是等价关系
基本数据结构
数据结构需要良好支持union和find操作，union操作相对简单，我们关注find操作。
find操作的特点及分析
find操作只要求当且仅当两个元素属于同一个集合时，作用在这两个元素上的find返回相同的集合名称。 由此自然想到树： 因为树的每一个元素都有相同的根，所以等价类可以用树表示，不相交集则以森林表示。树的根存储集合名称。 依照上述假设： find操作实质从指定节点向上找到根，所以只需要保存父链
可行数据结构（非唯一）
由于只需保存父链，不相交集类（森林）中的等价类（树）可以被非显示的存储在数组中，数组中元素有如下约定：
1、 数组中每个成员s[i]表示元素i的父亲，
2、 如果i是根，那么s[i]=-1.
图示说明
下图是隐示的森林示意图,上边是隐示森林数组，下边是依据该数组展现实际的森林。
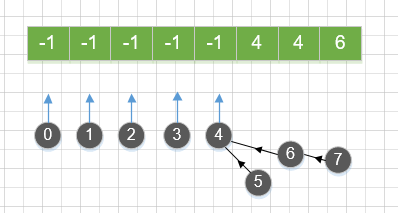隐示的森林示意图
按秩求并
为什么要使用？
任意合并会出现过深的树，所以采用按秩求并，它保证树的深度不超过O（logN）
如何实现？
1、 初始时为-1，
2、 仅当两颗相等深度的树求并时秩才增加；增加秩的操作实际为当前值-1
代码示意
/**
* 采用按秩求并
* @param root1 不相交集合1的根
* @param root2 不相交集合2的根
*/
public void union(int root1, int root2) {
if(s[root2]<s[root1]){
s[root1]=root2;
}else{
if(s[root1]==s[root2]){
s[root1]--;
}
s[root2]=root1;
}
}
图例说明
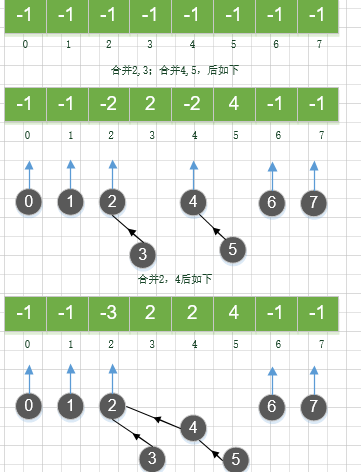按秩求并
路径压缩
为什么要使用？
不进行路径压缩，M次操作，容易出现最差情况O（MlogN），其中N为节点个数
如何实现？
1、 路径压缩用于find与union无关
2、 设操作find（x），此时路径压缩的效果是：
从x到根的路径上的每个节点都使其父节点为该树的根。
代码示意
/**
* 查找方式 ：路径压缩
* @param x 要寻找的元素
* @return x属于的集合
*/
public int find(int x) {
if (s[x] < 0) {
return x;
} else {
return s[x] = find(s[x]);
}
}
图例说明
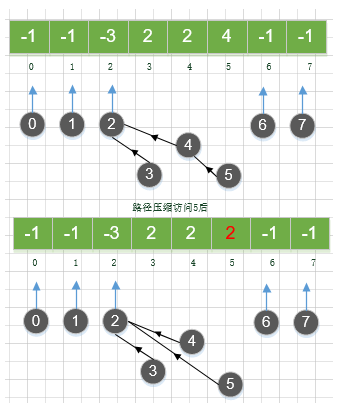
理论界限
M次union和find的运行时间为:
O(Mlog*N)
写在最后
什么你觉得太简单了，建议你试着证明！ 什么代码没有难度，可以实现各迷宫试试啊！