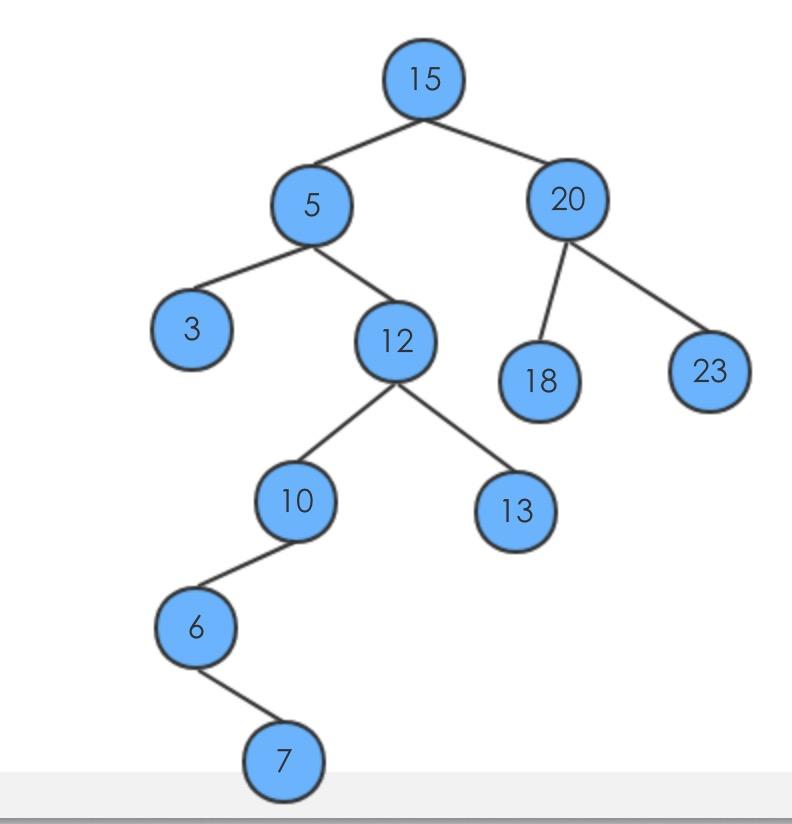
BST的性质
BST的形状为
- 每个BST中的节点x，存在一个key,一个指向父节点的parent指针，同时还有一个左子树和右子树
root的parent不存在
- 左子树值y与父节点x满足 key(y) <= key(x),右子树z满足 key(x) <=key(z)
插入实现机制
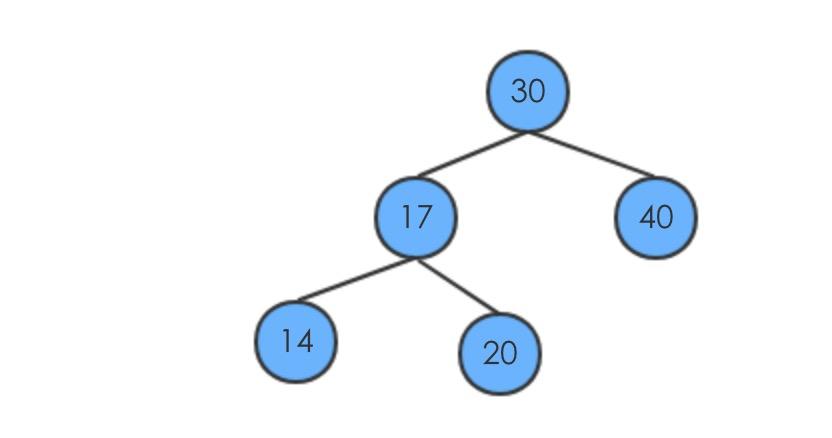
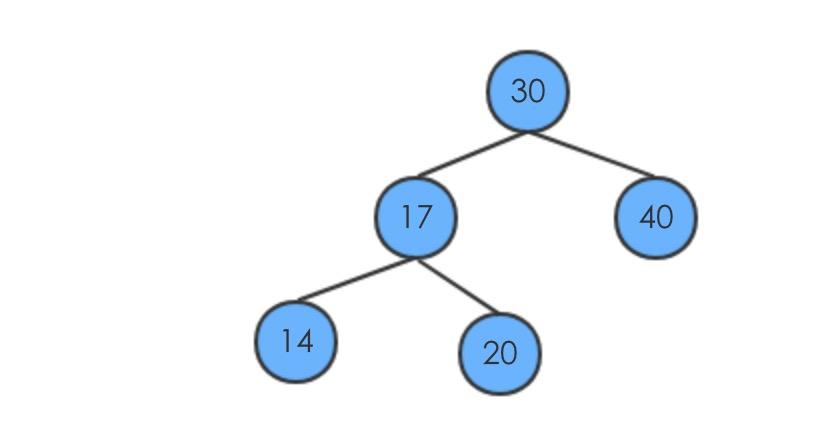
假设元素的插入顺序为30，40，17，20，14 刚开始的时候没有元素,插入新的元素
然后插入第二个元素40，它比30要大，置为它的右节点
插入第三个元素17，比30要小，置为它的左节点
然后是20，比30小，找到做子树，左子树的节点值为17，再次比较
最后一次元素再次插入，得到最终的BST结构
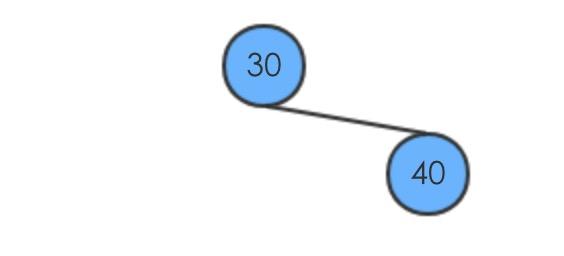
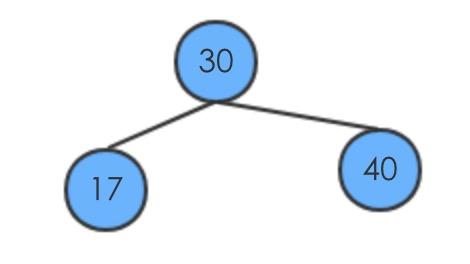
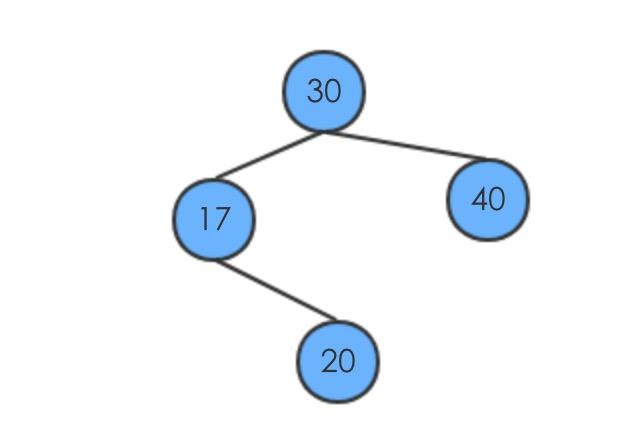
def insert(self,z):
x = self.root
y=None # x's parent
while x!=None :
//找到要插入的位置
y=x
if x.key <= z.key:
x=x.right
else:
x=x.left
if y == None:
//新插入的元素为第一个节点
self.root = z
z.parent = None
else:
//接入新的节点
z.parent = y
if y.key <= z.key:
y.right = z
else:
y.left = z
它的耗时为O(lgn)
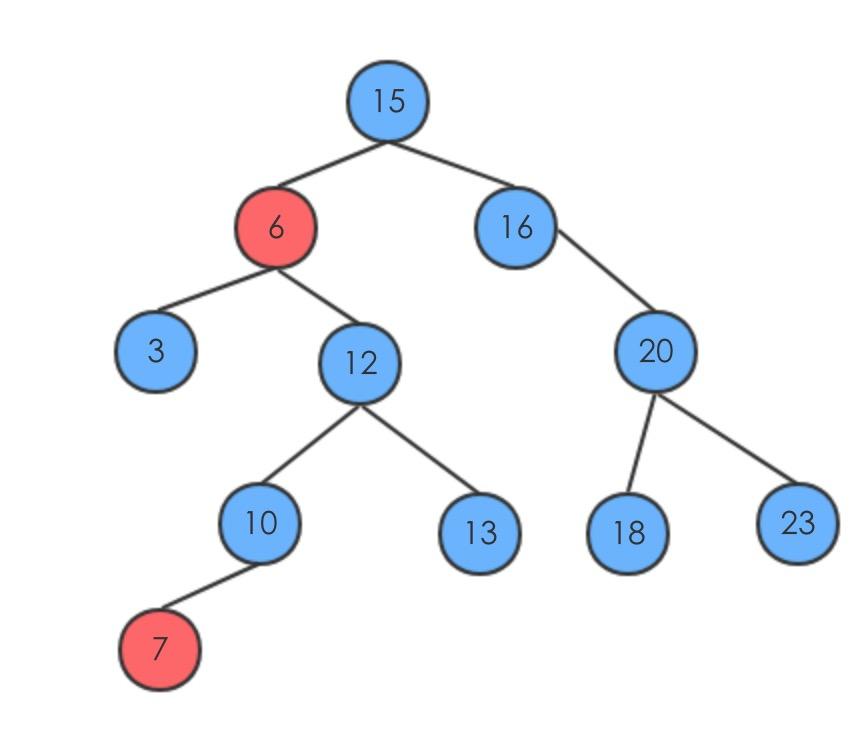
找到后继节点
后继节点即从值上来讲，找到比要找的元素要大最接近的值，根据BST的性质，它肯定在右子树上，所以如果存在存在右子树，就是右子树上的最小值，否则回溯到父节点，直到父节点不存在，或者遇到第一个不存在右节点关系的父子节点即得到后继值
17的后继是20，即17的右子树的节点；
20的后继是30，由于20没有右子树，会先回溯到17，然后17是它的父节点的左子树，那么它就是后继节点；
40的后继不存在；
def successor(self,node):
if node == None:
return None
if node.right != None:
# 后继一定在node的右节点
return self.minimum(node.right)
y = node.parent
# 后继节点只能在右节点
while y!=None and node == y.right:
node = y
y=y.parent
return y
最小值则一直递归到左子树没有节点即可
def minimum(self,node=None):
x = self.root if node == None else node
while x!=None and x.left!=None:
x = x.left
return x
删除节点
节点删除之后，必须要维持原有的BST性质
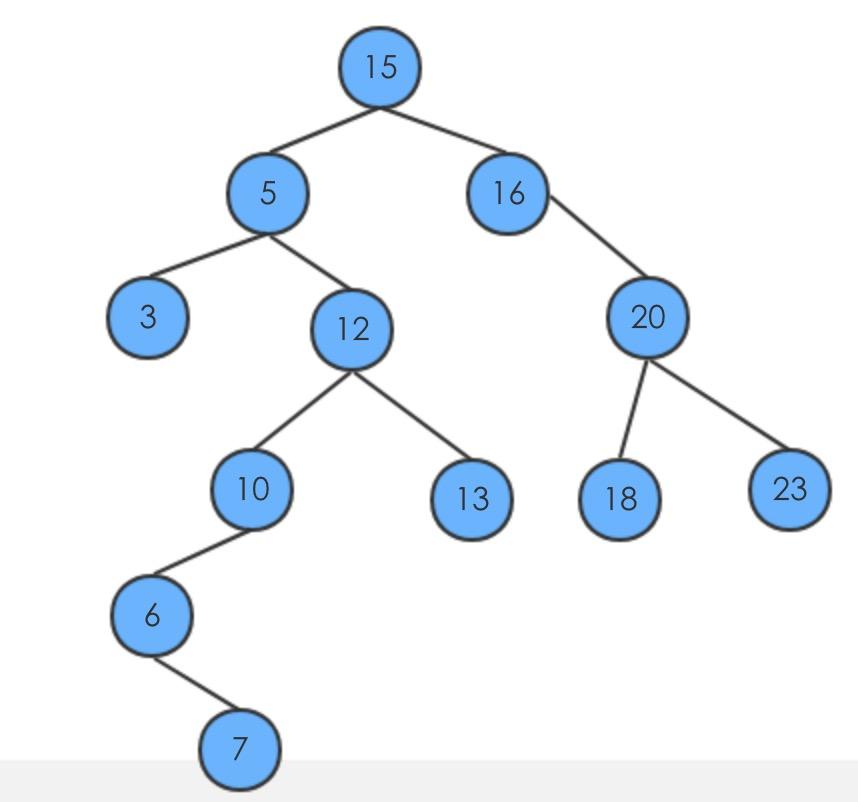
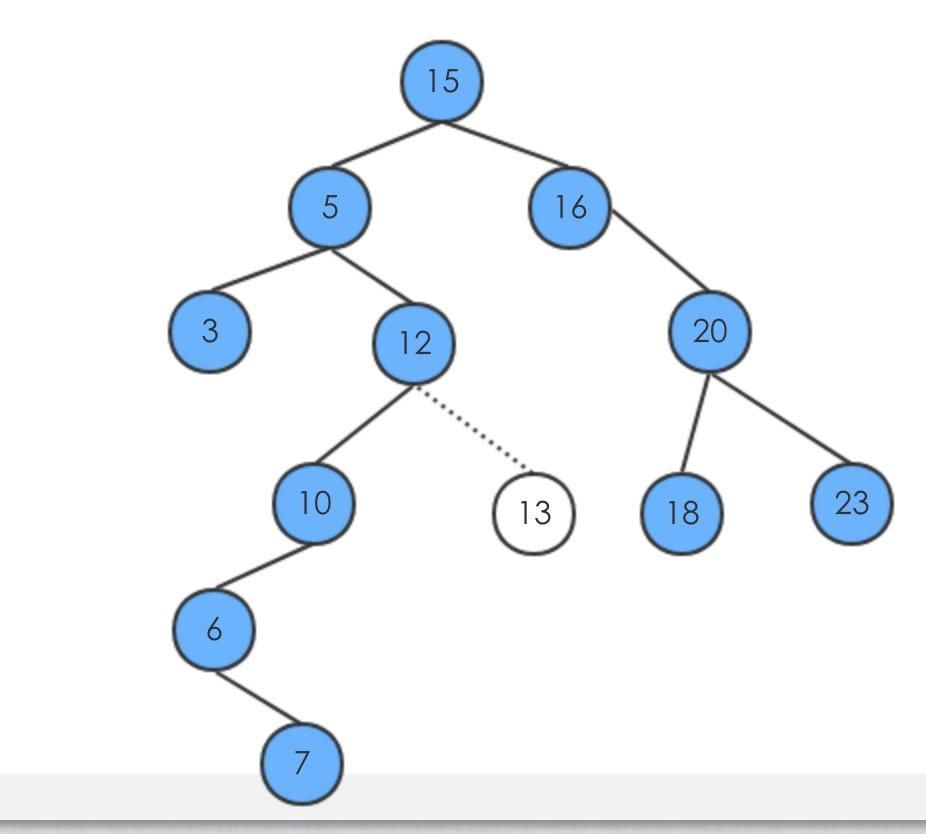
- 删除节点13，它一个子节点都没有，直接删除即可
- 删除节点16，只有右节点，直接有右节点替代即可
- 删除5，它既有左子树又有右子树，需要找到后继补上
def delete(self,node):
if node.left == None:
# 如果node.right 是None 相当于把要删的节点直接置成None,否则 后继者一定是第一个right值
return self.transplant(node,node.right)
elif node.right == None:
# node.left 一定存在，只需要替换节点之间的指针
return self.transplant(node,node.left)
else:
# 左子树和右子树都有，要维持BST的性质，必须找到后继节点
successor = self.minimum(node.right)
if successor != node.right:
# 最小的左边的值一定不存在
self.transplant(successor,successor.right)
# right有变化
successor.right = node.right
# 修改原来节点的父节点 node.right 一定存在
successor.right.parent = successor
self.transplant(node,successor)
successor.left=node.left
# 修改原子节点的父节点 node.left一定存在
successor.left.parent = successor
return node
指针变换关系为
def transplant(self,d,r):
""" d been delete r replecement"""
if d.parent == None:
self.root = r
elif d == d.parent.left:
d.parent.left = r
else:
d.parent.right = r
if r!=None:
r.parent = d.parent
return d