前提
假设总共有n个int元素,它的值在 {0,1,..,u-1}范围内,可以做到插入、删除、后继节点耗时为 lglgu 。
常用的应用场景如,网络路由表。对于IPV4来讲,u的取值范围是
。
如果u不是特别大,比如
,那么相当于总共的时间是 lglgn
lglgu 在什么样的场景下才会出现?
对于一个算法,如果它的迭代结构为
可以得到,它的耗时为O(lgk),那么要得到lglg的效果,相当于,迭代的结构为
使得lgk=u,有
此时算法的运行时间为 lglgu
如何使得u的存储和删除是常量时间?
使用数组存储所有的元素,数组的index就是要存储的n的值,数组u的值为0,表示当前值没有,1,表示有,这种结构为Bit Vector,如下:
上示中,u=16,目前存储的元素为 {1,9,10,15}
此时,存储和删除的时间都是O(1),查找后继节点的时间为O(u)
在bit vector的基础上,如何加快后继节点的查找速度?
把u分成
每个cluster的树的构建规则是根据每个值之间的或得到的结果,那么要查找对应的值是否存在,只需要看当前的cluster树的顶点是不是1即可
给每个cluster的树取名为summary
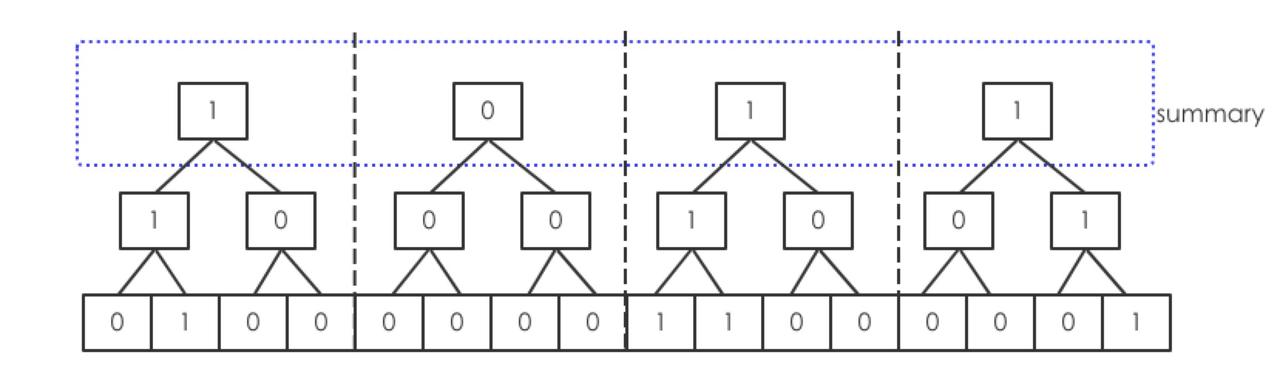
i表示在那个cluster,j表示在cluster中的位置,取函数 high(x)=i,low(x)=j
整个结构称作V,它包含如下信息
- V.cluster[i]大小为
,其中
- V.summary大小为
,从V.summary[i]能够判断 V.cluster[i]是不是空的
successor的获取方法为:
- 先看high(x)里面,耗时为
- high(x)里面没有找到下一个非空的cluster i ,耗时为
- 找到i的第一个存在的元素即可,耗时为
在此结构下,总的时间消耗
插入
Insert(V,x):
//先在u中插入元素
Insert(V.cluster[high(x)],low(x))
//更新summary
Insert(V.summary,high(x))
它的耗时为
可得,T(u)=O(lgu),没有达到预期的效果
查找后继
Successor(V,x):
//计算出在那个cluster
i=high(x)
//查找当前的cluster是不是有这个元素
j=Successor(V.cluster[i],low(x))
if j not exist:
//先找到i后面的非空的summary
i=Successor(V.summary,i)
//从找到的cluster中寻找后继者,Integer.MIN_VALUE表示我不知道具体的位置是那个
j=Successor(V.cluster[i],Integer.MIN_VALUE)
return index(i,j)
它的耗时为
即
总的耗时时间并不好,再次优化结构
在查找后继节点的过程中,如果当前的cluster不存在值,就找下一个cluster的元素j=Successor(V.cluster[i],Integer.MIN_VALUE),而根据后继节点的性质,当保存了每个cluster的最小元素的时候,这次查找就可以干掉。
其次,cluster查找的时候,如果能够立马知道,是否能够在当前cluster找到元素,那么就能决定,到底是找当前的clusterj=Successor(V.cluster[i],low(x))还是在下一个i=Successor(V.summary,i),当存储了每个cluster的max元素的下标的时候,如果low(x)<max显然就在当前cluster,否则就是下一个,这样只需要执行1次Successor
Successor(V,x):
//最小的元素只存储在V.min
if x < V.min:
return V.min
i=high(x)
if low(x) < V.cluster[i].max:
j=Successor(V.cluster[i],low(x))
else
i=Successor(V.summary,high(x))
j=V.cluster[i].min
return index(i,j)
它的耗时为
即T(u)=O(lglgu)
插入方式优化
Insert(V,x):
//先考虑V没有元素存在
if V.min == None
V.min=V.max=x
return
if x<V.min
swap(x,V.min)
if x>V.max
V.max=x
//如果当前cluster没有元素
if V.cluster[high(x)].min == None:
Insert(V.summary,high(x)) //第一次调用Insert,custer之前没有值,更新summary
Insert(V.cluster[high(x)],low(x)) //第二次调用Insert,在u中插入元素
当第一次调用去更新summary的时候,V.cluster[high(x)]肯定是没有值的,那么第二次调用 Insert(V.cluster[high(x)],low(x))的时候,只会执行
V.min == None这里只在V.min中存储了最小值 它的时间为 O(lglgu)
删除实际在这种方式下,它的耗时也是O(lglgu)
 。
。 ,那么相当于总共的时间是 lglgn
,那么相当于总共的时间是 lglgn




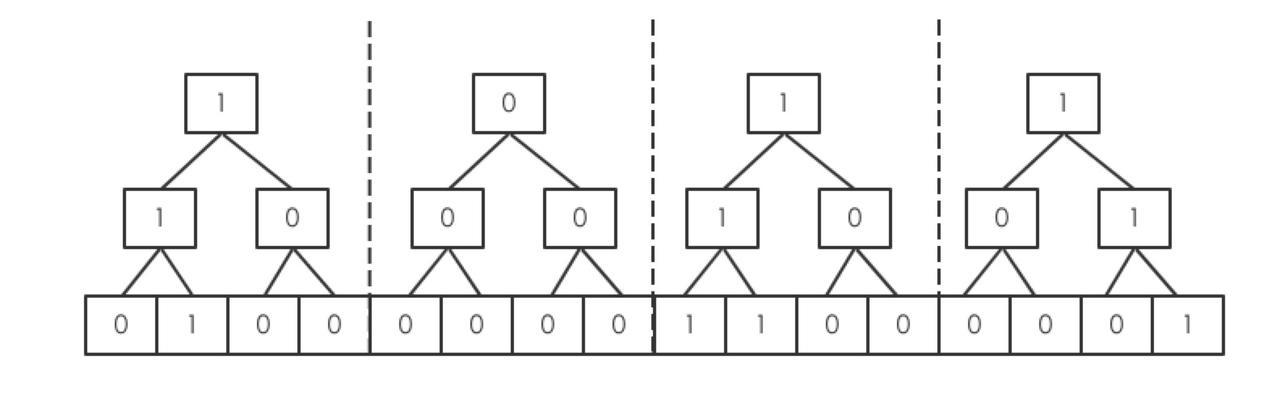

 ,其中
,其中 
 ,从V.summary[i]能够判断 V.cluster[i]是不是空的
,从V.summary[i]能够判断 V.cluster[i]是不是空的





