上一篇文章讲解了 红黑树的插入操作 ,这篇讲解一下红黑树的删除操作。
在讲解红黑树删除之前,先简单回顾下二叉树的删除操作。
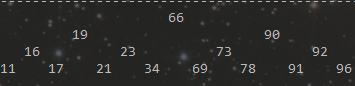
如果现在有一个二叉树如上图所示,我需要删除66这个节点该怎么做最快呢?
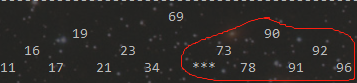
首先分析一下66这个节点的特点,在66的右边子树中,所有的节点都是比66大的。所以要想最快完成删除操作,只需要在右边子树中,找出一个最小的来,替换掉66即可。而真正从树上被剔除的节点,则是右子树中最小节点的位置。如图:
同样的思路,左边子树找出一个最大的替换也是可以的。当然如果被删除的节点本身左右两个子节点只有一个或者都没有值的话,那操作就更简单了,直接剔除即可。
下面开始分析红黑树的删除操作:
红黑树删除操作如下:
1、 根据二叉树的删除操作,找到真正需要从树上剔除的节点。
2、 如果需要剔除的节点为黑色,调整红黑树的平衡(调整步骤如下)。
那么调整平衡的时候,可能会遇到几种情况呢?其实不用说也应该知道,和插入操作的情形一样,理论上讲也是2种情况。
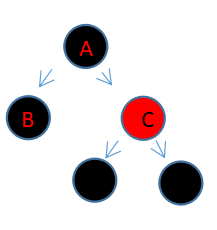
第一种情况,剔除节点(B)的兄弟节点(C)为红色(左下角为需要剔除的节点):
这种情况我们需要做的就是将兄弟节点(C)变为黑色,将父节点(A)变为红色,对父节点
进行右旋操作。将C的左子节点作为B的兄弟节点。
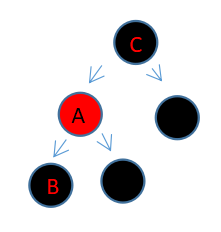
直接删除B的话,会导致A左右两边黑色节点数不一致。造成红黑树失去平衡。最好的办法就是把A的右边也删除一个黑色节点。但是因为B的兄弟节点C是红色,所以不能直接对C进行变色操作。所以只能将AC的颜色互换,然后对A进行右旋操作。将C的左子节点赋给B,作为B的兄弟节点,而因为C是红节点,红黑树不能出现连续两个红节点,所以C的子节点必然是黑色。
所以,经过一步调整,在不破换树平衡的情况下,我们就可以为B找到黑色的兄弟节点了。
接下来的操作遵循情况二即可。
第二种情况,剔除节点(B)的兄弟节点(C)为黑色(左下角为需要剔除的节点):
这种情况的话,可以分为两种子情况讨论。
首先,C节点的两个子节点都为黑色。如果是这种情况的话,操作就更简单了,直接将C节点变为红色,然后以剔除节点(B)的父节点A进行迭代判断即可。此处为什么要迭代呢?因为从A往下看他的左右两边虽然是平衡了,但是两个子分支都少了一个黑色节点,所以必然会导致树不平衡。如果A本身是红色的话,那直接将A改成黑色即可,如果A是黑色的话那就没办法了,只能以A为基准向上迭代判断。
然后如果C节点下面挂有红色节点该怎么办?(C节点不能直接变红)思路就是如果C节点下面挂有红色节点,我们应该想办法把红色节点挪到左边去,让他代替B节点,这样就可以直接调整到位,不破坏树的平衡。具体调整步骤如下:
将D和A节点设置为黑色,将C节点设置为A原来的颜色,然后对A进行左旋操作即可。
所以其实理解一下的话,红黑树还是很简单的。