122. 买卖股票的最佳时机 II

解题思路
方法1:暴力搜索
可能暴力搜索不能让有些面试官满意,但我觉得可以以搜索算法为起点,考虑更好的算法。
根据题意,没有限制交易次数,在每一天,我们就可以根据当前是否持有股票选择相应的操作,这里 “暴力搜索” 也叫 “回溯搜索”、“回溯算法”,首先画出树形图。
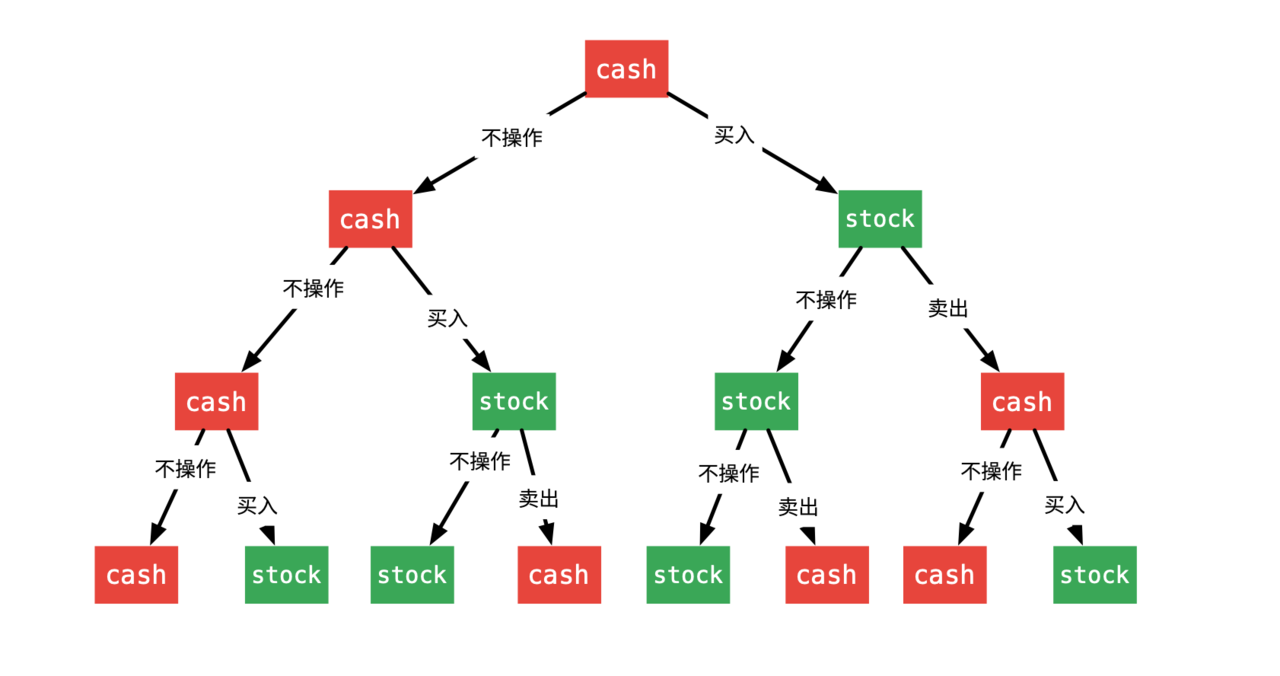
class Solution {
private int res;
public int maxProfit(int[] prices) {
if (prices == null || prices.length < 2) {
return 0;
} int len = prices.length; this.res = 0; dfs(prices, 0, len, 0, res); return this.res; } /** * @param prices 股价数组 * @param index 当前是第几天,从0开始 * @param status 0 表示不持有股票,1 表示持有股票 * @param profit 当前收益 */ private void dfs(int[] prices, int index, int len, int status, int profit) { // 递归终止条件 if (index == len) { this.res = Math.max(this.res, profit); return; } dfs(prices, index + 1, len, status, profit); if (status == 0) { // 可以尝试转向1 dfs(prices, index + 1, len, 1, profit - prices[index]); } else { // 此时 status == 1,可以尝试转向 0 dfs(prices, index + 1, len, 0, profit + prices[index]); } } }
超时在意料之中。注意看这个超时是在数据规模很大的时候,因此,可以说明搜索算法是正确的。
方法2:贪心算法
使用贪心算法的流程是这样的:
- 从第
i天(这里i >= 1)开始,与第i - 1的股价进行比较,如果股价有上升(严格上升),就将升高的股价(prices[i] - prices[i - 1])记入总利润,按照这种算法,得到的结果就是符合题意的最大利润。
下面对算法进行几点说明:
1、 该算法仅可以用于计算,但 计算的过程并不少真正交易的过程,但可以用贪心算法计算题目要求的最大利润。下面说明这个等价性:以 [1, 2, 3, 4] 为例,这4天的股价依次上身,按照贪心算法,得到的最大利润是:
# Java
res = (prices[3] - prices[2]) + (prices[2] - prices[1]) + (prices[1] - prices[0]);
= (prices[3] - prices[0]);
仔细观察上面的公式,按照贪心算法,在索引为 1、2、3 的这三天,我们做的操作应该是昨天买进的,今天卖出的,虽然这种操作题目并不允许,但是它等价于:“在索引为 0 的那一天买入,在索引为 3 的那一天卖出”。
1、 解释一下它为什么叫 “贪心算法”
贪心算法定义:
求解最优化的问题的算法通常需要经过一系列的步骤,在每个步骤都面临多种选择。对于许多最优化问题。使用动态规划算法来最优解有些杀鸡用牛刀了,可以使用更简单、更高效的算法。贪心算法(greedy algorithm)就是这样的算法。它在每一步都做出当时看起来最佳的选择,也就是说,它总数做出局部最优的选,寄希望这样的选择能导致全局最优解。
贪心算法在每一步总是做出在当前看来最好的选择。
因此
- “贪心算法” 和 “动态规划”、“回溯搜索”算法一样,完成一件事情,是分布决策的;
- “贪心算法”在每一步总是做出来当前看来最好的选择,这里理解“最好”的意思:
- “最好”的意思往往根据题目而来,可能是“最小”,也可能是“最大”;
- 贪心算法和动态规划相比,它即不看前面(也就是说它不需要从起那么的状态转移过来),也不看后面(无后效性,后面的选择不会对前面的选择有影响),因此贪心算法时间复杂度一般是线性的,空间复杂度是常数级别的。
- 这道题“贪心”的地方在于,对于“今天的股价 – 昨天的股价”,得到的结果有 3 种可能:(1)整数 (2)0 (3)负数。 贪心算法的决策是: 只加整数。
class Solution {
public int maxProfit(int[] prices) {
int res = 0;
int len = prices.length;
for (int i = 0; i< len - 1; i++) {
int diff = prices[i + 1] - prices[i]; if(diff > 0) { res += diff; } } return res; } }
等价写法:
class Solution {
public int maxProfit(int[] prices) {
int res = 0;
int len = prices.length;
for (int i = 0; i< len - 1; i++) {
int += Math.max(prices[i + 1] - prices[i], 0); } return res; } }
复杂度分享
- 时间复杂度:
O(N),这里N表示股价的数组长度。 - 空间复杂度:
O(1)
方法3:动态规划
想到动态规划的原因是:可以用贪心算法解决的问题,一般情况下都可以用动态规划。因此,不妨从“状态”、“状态转移方程”的角度考虑一下,使用动态规划的思路解决这道问题。
思路:
1. 定义状态
状态 dp[i][j] 定义如下:
- 第一维:
i表示索引为i的那一天( 具有前缀性质,即考虑了之前天数的收益)能获得的最大利润; - 第二维:
j表示索引为i的那一天持有股票,还是持有现金。这里0表示持有现金(cash),1表示持有股票(stock)。
2. 思考状态转移方程
- 状态从持有现金
(cash)开始,到最后一天我们关心的状态一谈是持有现金(cash); - 每一天状态可以转移,也可以不懂。状态转移用下图表示:
(状态转移方程写在代码中)
说明:
- 因为不限制交易次数,除了最后一天,每一天的状态可能不变化,也可能转移。
- 写代码的时候,可以不用对最后一天单独处理,输出最后一天,状态为
0的时候值即可。
3. 确定起始
起始的时候:
- 如果什么都不做,
dp[0][0] = 0; - 如果买入股票,当前收益是负数,即
dp[0][1] = -prices[i];
4. 确定终止
终止的时候,输出 dp[len - 1][0],因为一定有 dp[len - 1][0] > dp[len - 1][1]。
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
if (len < 2) return 0;
// 0:持有现金 // 1:持有股票 // 状态转移:0 -> 1 -> 0 -> 1 -> 0 -> 1 -> 0 int[][] dp = new int[len][2]; dp[0][0] = 0; dp[0][1] = -prices[0]; for (int i = 1; i < len; i++) { // 这两行调换顺序也是可以的 dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]); dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]); } return dp[len - 1][0]; } }
复杂度分析: 时间复杂度:O(N),这里 N 表示股价数组的长度。 空间复杂度:O(N),虽然是二位数字,但是二维是常数,与问题规模无关。
也可以将状态数组分开设置,语义更明确/
public class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
if (len < 2) {
return 0; } // cash:持有现金 // hold:持有股票 // 状态数组 // 状态转移:cash → hold → cash → hold → cash → hold → cash int[] cash = new int[len]; int[] hold = new int[len]; cash[0] = 0; hold[0] = -prices[0]; for (int i = 1; i < len; i++) { // 这两行调换顺序也是可以的 cash[i] = Math.max(cash[i - 1], hold[i - 1] + prices[i]); hold[i] = Math.max(hold[i - 1], cash[i - 1] - prices[i]); } return cash[len - 1]; } }
5. 考虑状态压缩
由于当前行只参考上一行,每一行就 2 个值,因此可以考虑使用“滚动变量”(“滚动数组”技巧)。
public class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
if (len < 2) {
return 0; } // cash:持有现金 // hold:持有股票 // 状态转移:cash → hold → cash → hold → cash → hold → cash int cash = 0; int hold = -prices[0]; int preCash = cash; int preHold = hold; for (int i = 1; i < len; i++) { cash = Math.max(preCash, preHold + prices[i]); hold = Math.max(preHold, preCash - prices[i]); preCash = cash; preHold = hold; } return cash; } }
复杂度分析
- 时间复杂度:O(N),这里 N 表示股价数组的长度。
- 空间复杂度:O(1),分别使用两个滚动变量,将一纬数组状态压缩到常数。
部分图片来源于网络,版权归原作者,侵删。


