前言
大家好，头回写博客，欢迎批评，以后我会尽量做到一个月2更，最近在重新温故算法。 今日提供读书笔记红黑树
目的
记录所学，温故知新
Java中对应的结构
TreeMap，以下是自己安装书中实现的原理，工作中应使用TreeMap
红黑树的定义
红黑树（Red Black Tree） 是一种自平衡二叉查找树.
红黑树和AVL树类似，都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡
时间界限与特点
红黑树的插入，删除操作在最坏情况下花费
log N
红黑树是具有如下着色性质的二叉查找树：
1、 每个节点要么着成红色，要么着成黑色
2、 根是黑色的
3、 如果一个节点是红色，那么他的子节点必须是黑色
4、 从一个节点到一个null引用，每一条路径必须包含相同数目的黑色节点。
使用该着色法则，保证红黑树的高度最多为：
2*log (N+1)
插入操作
自底向上插入及遇到的问题
自底向上插入
如果新插入的项的父节点是黑色，那么插入结束，默认新插入的节点是红色的.
如果父亲是红色的，就有几种情形（每种都有对称形式，假设父亲是曾祖父的左儿子）.
- 父亲的兄弟是黑色，
如下图:
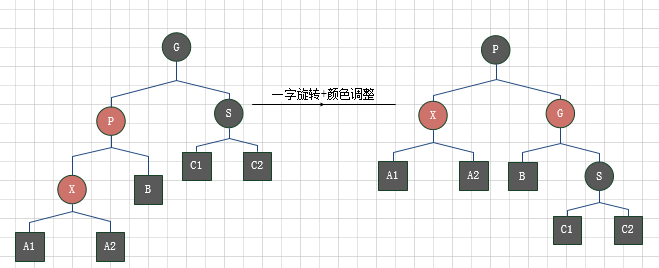父亲的兄弟是黑色的调整示意图
-
- 曾祖父为黑色,当前节点为父亲的右儿子且为红色.
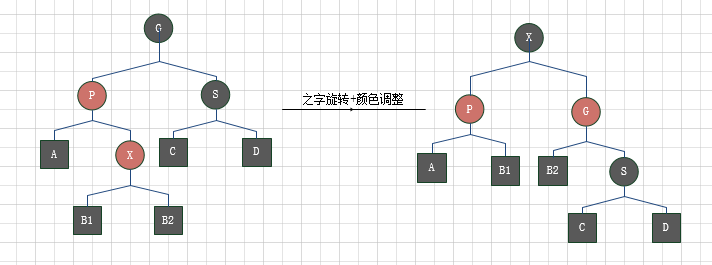父亲的兄弟是黑色并且父亲的右儿子为红色
- 父亲的兄弟是红色时， 需要进行上滤 如下图过程:
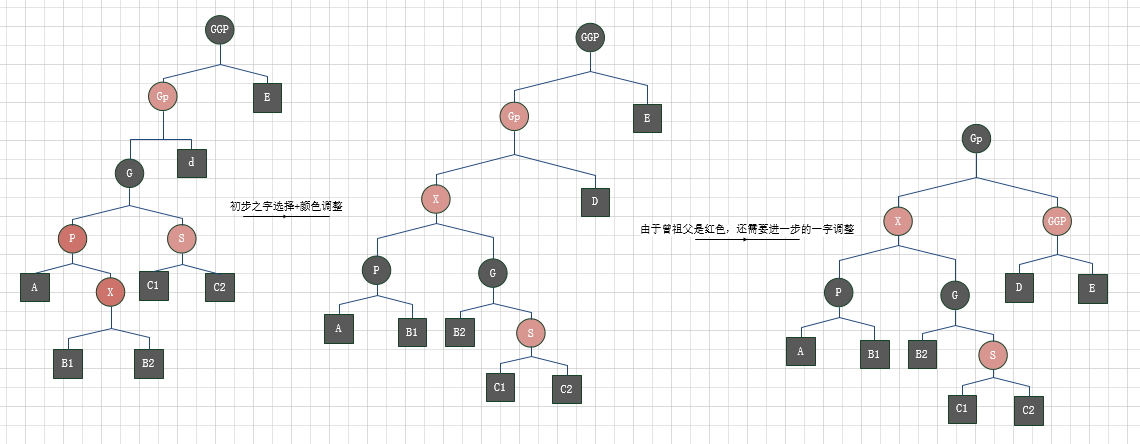进行上滤的示例
遇到的问题
上滤需要一个栈或者保持父链来实现，并且过程复杂.
自顶向下插入
概念：在向下的过程中如果看到一个节点current有两个红儿子，可将该节点呈红色，两个儿子变为黑色。
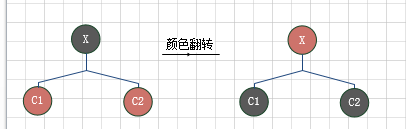红黑树颜色翻转
当current节点的父亲parent也是红色时候，进行适当的选择，以该方式向下进行插入操作屏蔽了X节点的兄弟节点也是红色的可能. 代码：
/**
* 自顶向下插入
*/
public void insert( AnyType item ){
nullNode.element=item;
current=parent=grand=header;
//自顶向下调整,避免插入的父节点和父节点的兄弟节点为黑色的情况，该情况复杂不利于恢复平衡信心.
while(compare(item,current)!=0){
great=grand;
grand=parent;
parent=current;
current=compare(item,current)<0?current.left:current.right;
if(current.left.color==RED&¤t.right.color==RED){
handleReorientAfterInsert(item);
}
}
if(current!=nullNode){//重复元素跳过
return;
}
//找到位置
//构建新的节点
current=new RedBlackNode<AnyType>(item,nullNode,nullNode);
//维护与父节点的关系
if(compare(item,parent)<0){
parent.left=current;
}else{
parent.right=current;
}
//插入完成后,维护平衡信息
handleReorientAfterInsert(item);
nullNode.element=null;
}
/**
* 插入后维护平衡信息
* @param item
*/
private void handleReorientAfterInsert(AnyType item) {
//初步调整的变换颜色 自己变为红色，两个儿子变为红色
current.color=RED;
current.left.color=BLACK;
current.right.color=BLACK;
if(parent.color==RED){
//调整后破坏了红黑树性质，需要旋转
//分两种类型 一字形和之字形，之字形比一字形调整了多一步
grand.color = RED;
if((compare(item,grand)<0)!=(compare(item,parent)<0)){//之字形
parent=rotate(item,grand);
//调整parent和他的儿子，并将调整后的节点W设置成parent
}
//调整完成，重新设置当前节点
current=rotate(item,great);
//并将当前节点设置为黑色
current.color=BLACK;
}
//保证根节点是黑色
header.right.color=BLACK;
}
自顶向下删除
- 删除操作归结于可以删除红色的树叶；
- 如果要删除的节点有右儿子，以右儿子的最小元内容替换要删除节点内容，之后删除右儿子最小元来进行删除。
- 如果只有左儿子，以左儿子最大元内容替换要删除节点的内容，之后删除左儿子最大元
- 如果要删除的节点没有儿子， 将该节点调整成红色，将父节点对应的引用设置成nullNode
- 3.如果没有儿子
-
- 若父节点为header,将树变为空树
-
- 否则如果当前节点为黑色，进行调整，保证删除项为红色，之后将要删除项的父节点的引用设置为nullNode.
红色树叶删除简单，如果要删除的是黑色分为如下几种情：
1、 X与兄弟T的儿子都是黑色
![68\_5.png][68_5.png] X与兄弟T的儿子都是黑色
2、 X的儿子是黑色，兄弟T有一个左儿子是红色
![68\_6.png][68_6.png] X的儿子是黑色，兄弟T有一个左儿子是红色
3、 X的儿子是黑色，兄弟T有一个右儿子是红色
![68\_7.png][68_7.png] X的儿子是黑色，兄弟T有一个右儿子是红色
4、 X的儿子是黑色，兄弟T儿子都是红色
![68\_8.png][68_8.png] X的儿子是黑色，兄弟T儿子都是红色
以上每种情形都有与只对应的对称类型。如果X节点是红色，我们生产新的X,P,T向下探索 相关代码：
/**
* 删除一个节点，
* 依据可以删除一个叶子,
* 自顶向下删除,
* 1如果要删除项有右儿子，先删除右儿子最小项，之后使用原右儿子的最小项内容替换要删除项的内容.
* 2.如果只有左儿子，先删除左儿子最大，之后使用左儿子的最大项替换要删除项的内容.
* 3.如果没有儿子
* 若父节点为header,将树变为空树
* 否则如果当前节点为黑色，进行调整，保证删除项为红色，之后将要删除项的父节点的引用设置为nullNode.
* @param x
*/
public AnyType remove( AnyType x ){
//需要自己尝试书写
//先查找是否存在，存在后删除
RedBlackNode<AnyType>p=find(x);
RedBlackNode<AnyType>pParent=parent;
if (p == null){
return null;
}
AnyType item=p.element;
//自顶向下删除
//找到后,如果存在左儿子和右儿子（或 只有右儿子），
//使用右儿子的最小，替换当前 ，之后删除右儿子最小
//只有左儿子使用左儿子最大替换，
RedBlackNode<AnyType>replacement=findReplaceMent(p);
if(replacement!=null){
//进行替换
p.element=remove(replacement.element);
}else{
//没有替换者，
if(pParent==header){
makeEmpty();
}else{
if(p.color==BLACK){
//将p地调整为红色
fixbeforedelete(p.element) ;
pParent=parent;
}
//调整为删除
if(pParent.left==p){
pParent.left=nullNode;
}else if(pParent.right==p){
pParent.right=nullNode;
}
}
}
current=p;
parent=pParent;
return item;
}
/**
* 删除前调整数的平衡信息，保证要删除的项是红色
* @param item
*/
private void fixbeforedelete(AnyType item) {
grand=header;
RedBlackNode<AnyType>p=header.right;
RedBlackNode<AnyType>x=nullNode;
RedBlackNode<AnyType>t=nullNode;
RedBlackNode<AnyType>i=find(item);
//先把p涂成红色，最后恢复
p.color=RED;
x=item.compareTo(p.element)<=0?p.left:p.right;
t=item.compareTo(p.element)<=0?p.right:p.left;
//保证要删除的项是红色
while(i.color!=RED){
if(x.color==RED||
(x.color==BLACK&&(x.left.color==RED&&x.right.color==RED)||
t.color==BLACK&&(x.left.color==RED||x.right.color==RED))
){
//x为红色或x儿子为红色,x为黑色&&t为黑色,x有一个儿子为红色,向下探索
grand=p;
p=x;
x=item.compareTo(p.element)<0?p.left:p.right;
t=item.compareTo(p.element)<0?p.right:p.left;
}else if(x.color==BLACK&&t.color==BLACK
&&x.right.color==BLACK&&x.left.color==BLACK){
//3中情况需要，调整的情况
if(t.left.color==BLACK&&t.right.color==BLACK){
//t的两个儿子，直接变换p和t,x的颜色，重新再该位置下探
p.color=BLACK;
t.color=RED;
x.color=RED;
}else if(t.left.color==RED&&t.right.color==RED){
//t有两个红色的儿子，调整后下探
if(p.right==t){
RedBlackNode<AnyType>red=t.left;
p.right=red.left;
t.left=red.right;
red.right=t;
red.left=p;
//更新祖父节点
if(grand.left==p){
grand.left=red;
}else{
grand.right=red;
}
grand=red;
p.color=BLACK;
x.color=RED;
t=p.right;
}else{
RedBlackNode<AnyType>red=t.right;
p.left=red.right;
t.right=red.left;
red.right=p;
red.left=t;
if(grand.left==p){
grand.left=red;
}else{
grand.right=red;
}
grand=red;
p.color=BLACK;
x.color=RED;
t=p.left;
}
}else if(p.right==t&&t.left.color==RED){
//右左，之字调整后继续下探
RedBlackNode<AnyType>red=t.left;
p.right=red.left;
t.left=red.right;
red.right=t;
red.left=p;
if(grand.left==p){
grand.left=red;
}else{
grand.right=red;
}
grand=red;
p.color=BLACK;
x.color=RED;
t=p.right;
}else if(p.left==t&&(t.right.color==RED)){
//左右，之字调整后继续下探
RedBlackNode<AnyType>red=t.right;
p.left=red.right;
t.right=red.left;
red.right=p;
red.left=t;
if(grand.left==p){
grand.left=red;
}else{
grand.right=red;
}
grand=red;
p.color=BLACK;
x.color=RED;
t=p.left;
}else if(p.right==t&&t.right.color==RED){
//右右 一字，交换t和p
p.right=t.left;
t.left=p;
if(grand.left==p){
grand.left=t;
}else{
grand.right=t;
}
grand=t;
t.color=RED;
p.color=BLACK;
t=p.right;
}else if(p.left==t&&t.left.color==RED){
//左左 一字 交换t和p
p.left=t.right;
t.right=p;
if(grand.left==p){
grand.left=t;
}else{
grand.right=t;
}
grand=t;
t.color=RED;
p.color=BLACK;
t=p.left;
}
}else if(x.color==BLACK&&p.color==BLACK&&t.color==RED){
//x的兄弟为黑色，x和x的父节点都是红色，调整t和p,保证p为红色后，继续下探
if(p.left==x){
p.right=t.left;
t.left=p;
if(grand.left==p){
grand.left=t;
}else{
grand.right=t;
}
grand=t;
t.color=BLACK;
p.color=RED;
t=p.right;
}else{
p.left=t.right;
t.right=p;
if(grand.left==p){
grand.left=t;
}else{
grand.right=t;
}
grand=t;
t.color=BLACK;
p.color=RED;
t=p.left;
}
}else if(header.right==p&&x.color==BLACK
&&p.color==RED&&t.color==RED){
p.color=BLACK;
}
}
header.right.color=BLACK;
parent=p;
}
总结
1、 红黑树的操作在最坏情况下花费
log N
1、 插入操作采用自顶向下操作保证要插入的节点的父亲是黑色。
2、 删除操作采用自顶向下操作保证要删除的节点为红色。